Paramagnetism in the Conduction Electrons in Metals

PARAMAGNETISM IN THE CONDUCTION ELECTRONS IN METALS

According to Langevin's theory the paramagnetic susceptibility is inversely proportional to the temperature. However, some metals have been found to exhibit paramagnetism independent of temperature.

It was. W. Pauli (1927) who demonstrated that this is due to paramagnetism of free electrons (that constitute the electron gas), since they can orient only in two directions, either along the magnetic field or against it.

In order of tog understand the existence of Pauli paramagnetism, let us recall the curve between density of states versus energy (Fig. 2.27) at absolute zero of temperature. That curve may be split into two parts with spins pointing in the +ve z-direction and other with spin in the opposite direction, as shown in Fig. 2.27(a).

In the absence of an external magnetic field, the distribution of electrons with spins parallel to z-direction is equal to the number of electrons with opposite spins and hence the net magnetic moment of the electron gas is zero.

When a magnetic field (B) is applied along the z-direction, the energy of the spins aligned parallel to B is lowered by the amount μB' while the energy of the spins opposite to B is raised by the same amount (Fig. 2.27(b)).

As a result of this, the Fermi level for the two spin distributions shift with respect to each other and give rise to energetically unstable situation.

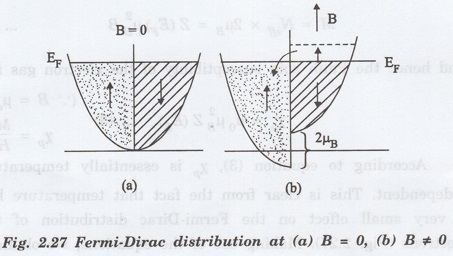
In order to acquire the stable configuration, the electrons lying near the Fermi level with antiparallel spins flip into the region of parallel spins until the two Fermi levels become equal s become again (Fig 2.27(b)).

The number of electrons which effectively change their direction is equal to the density of states at the energy level (Z (E_F)) in one of the spin distribution times the change in energy, i.e.

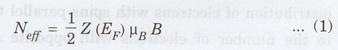
where the factor 1/2 is due to the fact that the density of states of one spin distribution is half of the total density of states. μ_B is magnetic moment of electron.

Thus after the application of the field, the number of electrons with spins parallel to the field is greater than the electrons with opposite spin by N_eff, to a net magnetization.

Since each flip increases the magnetization by 2 μ_B (from -μ_B to +μ_B), the net magnetization is given by

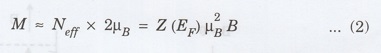
and hence the Pauli spin susceptibility of the electron gas is

According to equation (3), χ_P, is essentially temperature independent. This is clear from the fact that temperature has a very small effect on the Fermi-Dirac distribution of the electrons (Fig. 2.27). Making use of the equations, we obtain

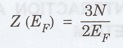
N - No. of electrons per unit volume.

so that (3) becomes,

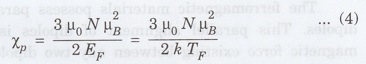
 where E_F = kT_F. This equation can be rewritten in terms of the classical susceptibility as

where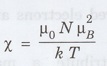 

Since T_F is normally very high, χ_p, is smaller than χ by about two orders of magnitude, which is in agreement with the experimental results. In transition metals, the paramagnetic susceptibility, χ_p is exceptionally high, because Z (E_F) is large.