Transformation Ratio

TRANSFORMATION RATIO (K)

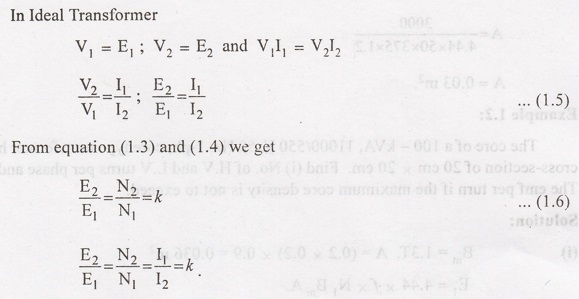
'k' is called transformation ratio.

If N₂ > N₁. i.e., k> 1, then transformer is a step up transformer.

If N₂ < N₁. i.e., k < 1, then transformer is a step down transformer.

Example 1.1:

The maximum flux density in the core of a 250/300 V, 50 Hz single phase transformer is 1.2 Wb/m². If the emf per turn is 8 volt, determine (i) Primary and Secondary turns, (ii) Area of the core.

Solution:

(i) E₁ = N₁ × emf induced/turn

E₁ = 250/8 = 32; N₂ = 3000/8 = 375.

(ii) We may use

E₂ = 4.44 ƒN₂ Bm A

Example 1.2:

The core of a 100 - kVA, 11000/550 V, 50 Hz, 1-ph, core type transformer has a cross-section of 20 cm x 20 cm. Find (i) No. of H.V and L.V turns per phase and (ii) The emf per turn if the maximum core density is not to exceed.

Solution:

Keeping supply frequency constant, if primary voltage is increased by 10%, magnetizing current will increase by much more than 10%. However, due to saturation, flux density will increase only marginally and so will the eddy current and hysteresis losses.

Example 1.3:

A single phase transformer has 400 primary and 1000 secondary turns. The net cross sectional area of the core is 60 cm₂. If the primary winding be connected to a 50 Hz supply at 520 V. Calculate (i) the peak value of flux density in the core, (ii) the voltage induced in the secondary winding.

Solution:

Example 1.4:

The core of a three phase, 50 Hz, 11000/550 V delta/star, 300 kVA, core type transformer operates with a flux of 0.05 wb. Find

(i) Number of H.V and L.V turns per phase.

(ii) emf per turn.

(iii) Full load HV and LV phase currents.

Solution: Maximum value of flux has been given as 0.05 wb:

(i) emf per turn = 4.44 f φ_m = 4.44 × 50 × 0.05 = 11.1 Volts.

(ii) Calculations for number of turns two sides:

Voltage per phase on delta-connected primary winding = 11,000 V

Voltage per phase on star connected secondary winding = 550/1.732 = 317.5 Volts.

T1 = Number of turns of primary, per phase = Voltage per phase/emf per turn = 11,000/11.1 = 991.

T2 = Number of turns on secondary, per phase = Voltage per phase/emf per turn = 317.5/11.1 = 28.6 = 30.

Note:

Generally, low voltage turns are calculated first, the figure is rounded off to next higher even integer. In this case it will be 30. Then, number of turns on primary side is calculated by turns-ratio.

T₁ = T₂ (V₁ / V₂) = 30 x 11,000/317.5 = 1040.

It will reduces the flux and result into less saturation.

(iii) Full load HV and LV phase currents.

Output per phase = 300/3 = 100 kVA

Example 1.5:

A single phase transformer has 500 turns in the primary and 1200 turns in the secondary. The cross sectional area of the core is 80 sq.cm. If the primary winding is connected to a 50 Hz supply at 500V, Calculate (i) peak flux density, (ii) voltage induced in the secondary.

Solution: Emf equation of transformer

E₁ = 4.44 f φ_m N

500 = 4.44 × 50 × φ_m × 500

Example 1.6:

A 25 kVA, single-phase transformer has 250 turns on the primary and 40 turns on the secondary winding. The primary is connected to 1500 volt, 50 Hz mains. Calculate,

(i) Primary and Secondary currents on full load

(ii) Secondary emf

(iii) Maximum flux in the core.

Solution:

(i) V₂ = Secondary voltage rating = Secondary emf

V₂ / 1500 = 40 / 250, going V₂ = 240 volts

(ii) Primary current = 25,000/1500 = 16.67 A

Secondary current = 25000/240 = 104.2 A.

(iii) If φ_m is the maximum core flux in wb,

1500 = 4.44 x 50 x φ_m x 250

φ_m = 0.027 wb (or) 27 m wb.