Operations on Signals

OPERATIONS ON SINGALS

Independent variable "t" of a continuous time signal or "n" of a discrete time signal can be varied by anyone of the following operation.

i. Time delay (or) Time advancing

ii. Time folding

iii. Time scaling.

Similarly amplitude of CT signal or DT signal can be varied by

iv. Amplitude scaling

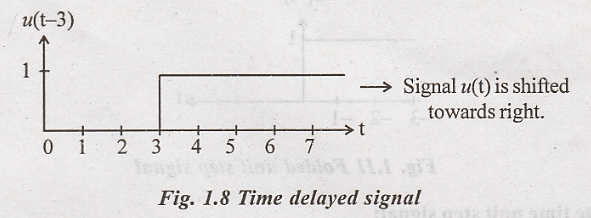
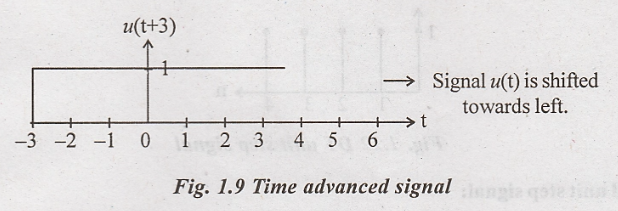
Time Delay/Time Advancing

i. In time delay, signal is shifted towards right side

ii. In time advance, signal is shifted towards left side.

Following example shows the time delay and time advancing operations on continuous time (CT) and discrete time (DT) unit step signal.

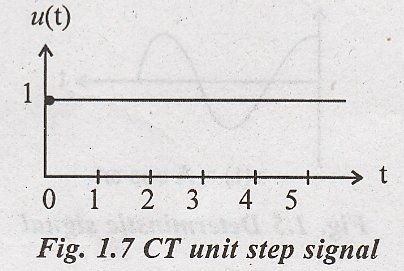
Continuous time unit step signal

Time delay of x(t) [Shifting right]

Time advance of x(t) [Shifting left]

Time Folding

Time folding of continuous time signal x(t) or discrete time signal x(n) is reflected version of x(t) (or) x(n).

Time folding signal is obtained by replacing t by -t (or) n by-n.

Following example shows the time folding operation on CT & DT signals.

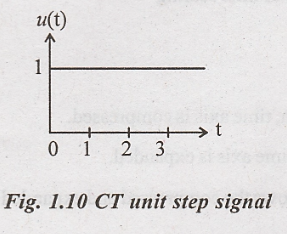
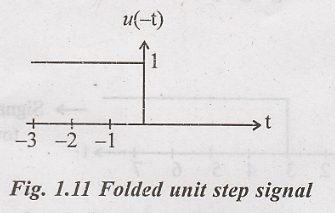
Continuous time unit step signal:

Folded unit step signal:

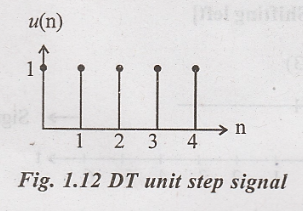
Discrete time unit step signal:

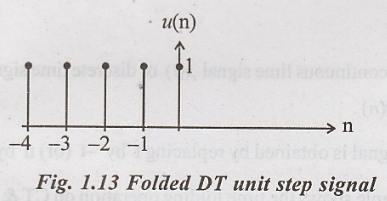
Folded unit step signal:

Time Scaling

There are two types of time scaling

i. Time compression

ii. Time expansion.

In time compression, time axis is compressed.

In time expansion, time axis is expanded.

Following figure shows the compressed and expanded continuous time signal.

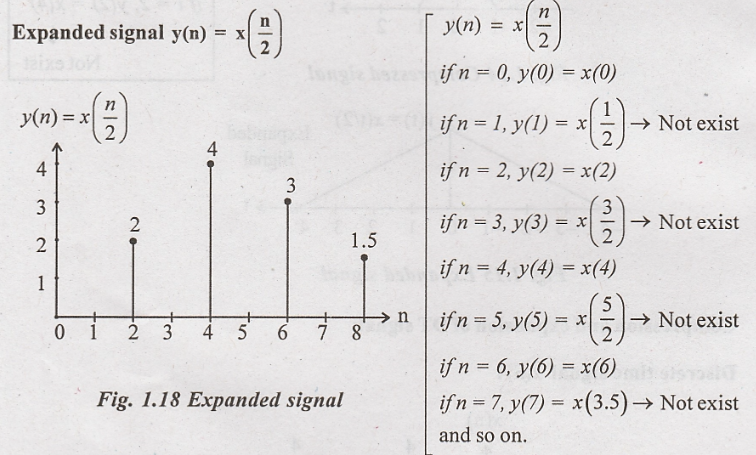
Compression and expansion of DT signal

Discrete time signal x(n)

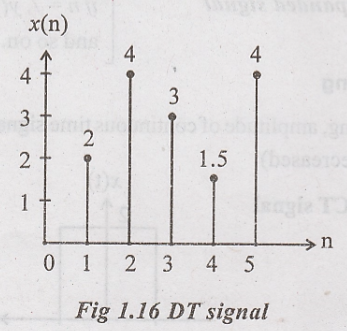
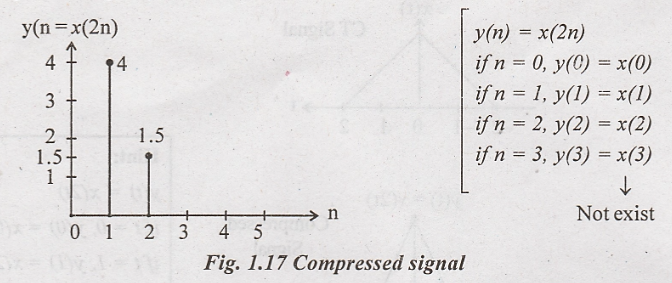
Compressed signal y(n) = x(2n)

Amplitude Scaling

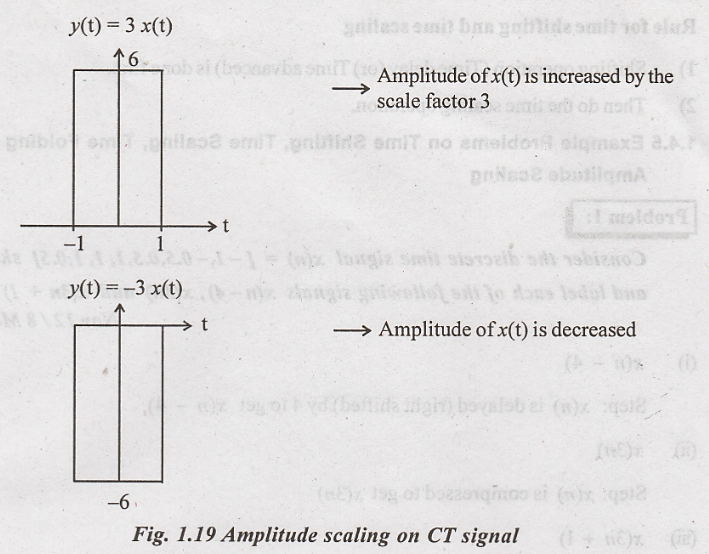
In amplitude scaling, amplitude of continuous time signal or discrete time signal is varied. (Increased or Decreased)

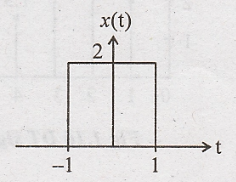
Amplitude scaling on CT signal

Amplitude Scaling on discrete time signal :

Rule for time shifting and time scaling

1) Shifting operation (Time delay (or) Time advanced) is done first.

2) Then do the time scaling operation.

Example Problems on Time Shifting, Time Scaling, Time Folding and Amplitude Scaling

Problem 1:

Consider the discrete time signal x(n) = [-1,-0.5,0.5, 1, 1, 1,0.5] sketch and label each of the following signals x(n-4), x(3n) and x(3n + 1) Nov. 12/8 Marks

(i) x(n - 4)

Step: x(n) is delayed (right shifted) by 4 to get x(n = 4).

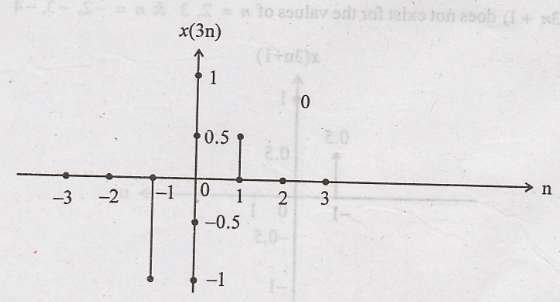
(ii) x(3n)

Step: x(n) is compressed to get x(3n)

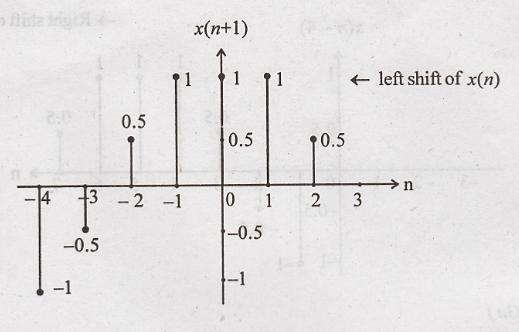
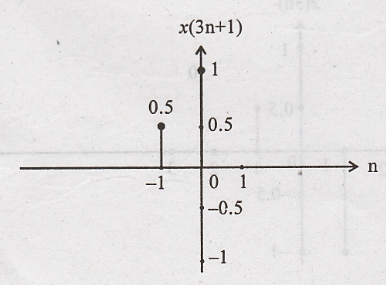
(iii) x(3n+1)

Step 1: x(n) is advanced (left shift) by 1 to get x(n + 1)

Step 2: x(n + 1) is compressed by 3 to get x(3n+ 1)

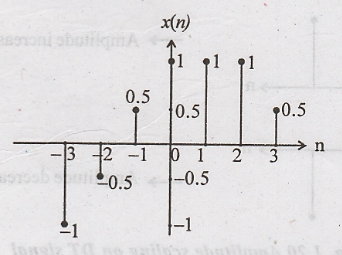
x(n) = [-1,-0.5,0.5, 1, 1, 1,0.5]

↑

Arrow mark represents the value of n = 0

x(n) :-

(i) x(n-4)

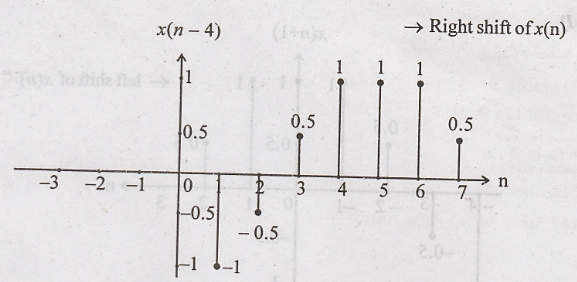
(ii) x(3n)

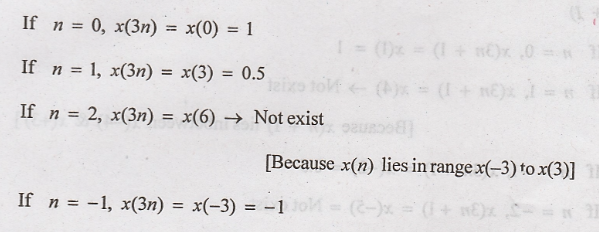
(iii) x(3n+1)

x(n+1)

x(3n+1)

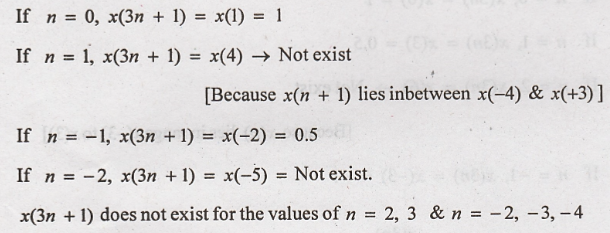
Problem 2:

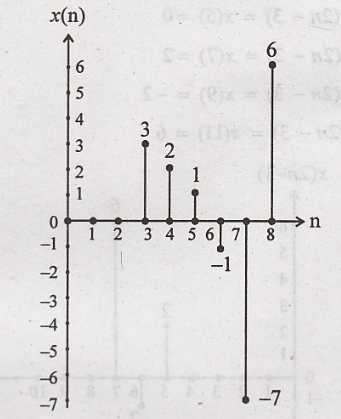
If the discrete time signal x(n) = {0, 0, 0, 3, 2, 1, -1, -7, 6} then find y(n) = x(2n-3) Nov. 2007- 2 Marks

Solution:

x(n)

x(n-3)

x(n) is delayed (right shift) by 3 to get x(n-3)

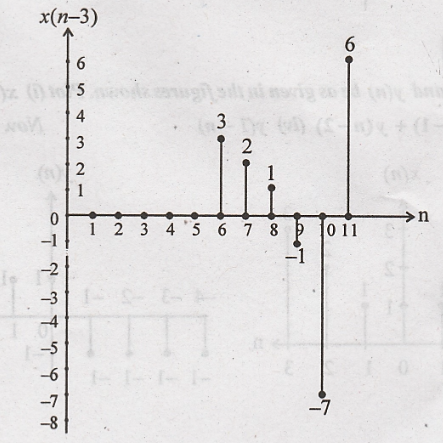
x(2n-3)

x(n-3) is compressed by 2

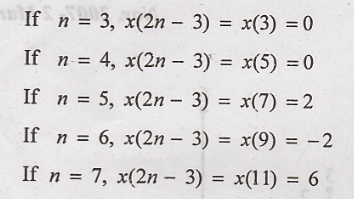
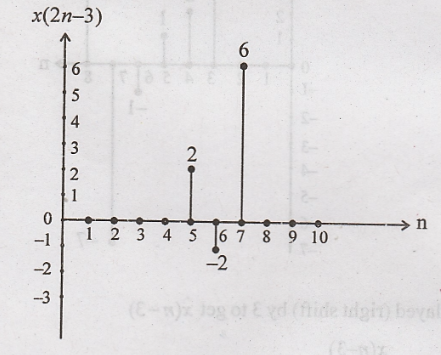
Problem 3:

Let x(n) and y(n) be as given in the figures shown. Plot (i) x(2n) (ii) x(3n-1) (iii) x(n-1) + y(n−2) (iv) y(1 − n)

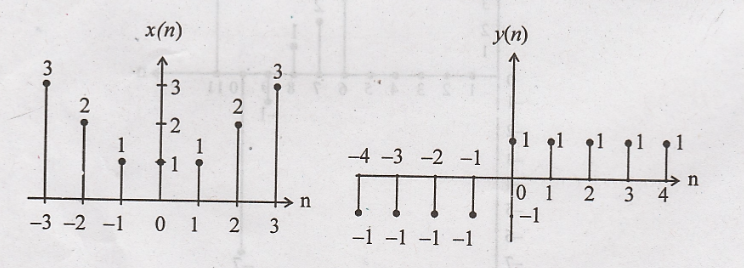
Solution :

x(2n) ⇒ x(n) is compressed by 2 to get x(2n).

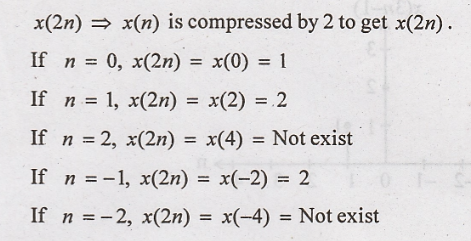
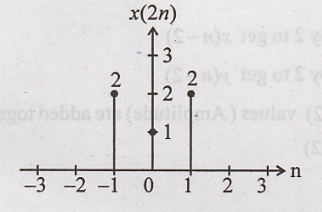
(ii) x(3n-1)

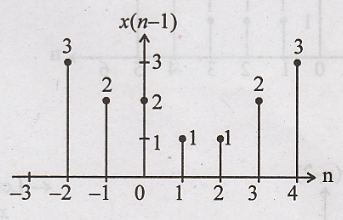
Step 1: x(n) is delayed (Right shift by 1 to get x(n − 1)

Step 2: x(n - 1) is compressed by 3 to get x(3n - 1)

x(3n - 1)

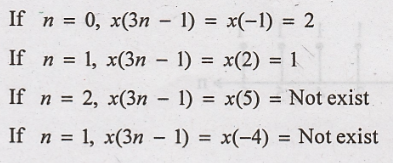
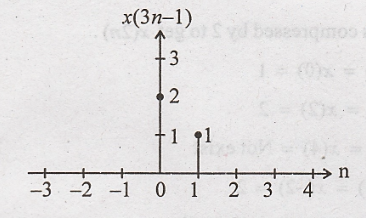
(iii) x(n-2) + y(n-2)

Step 1: x(n) is delayed by 2 to get x(n-2)

Step 2: y(n) is delayed by 2 to get y(n-2)

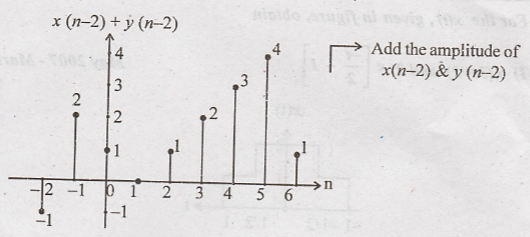
Step 3: x(n-2) & y(n-2) values (Amplitude) are added together to get x(n-2) + y(n-2)

x(n-2)

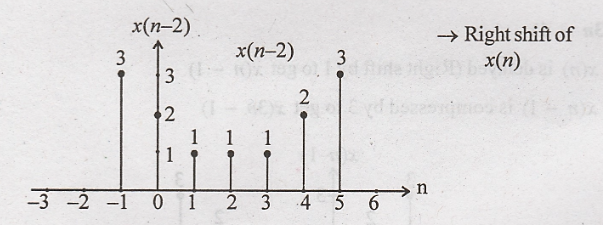
y(n-2)

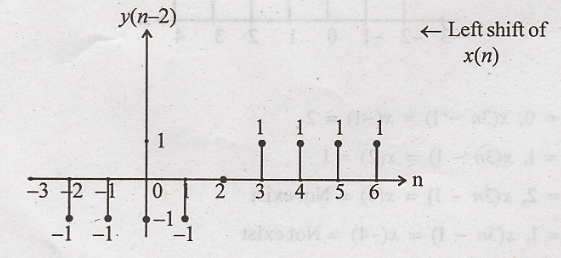
x(n-2) + y(n-2)

(iv) y(1-n)

We can write y(1-n) as y(-n + 1)

Step 1: y(n) is advanced (left shift)

Step 2: y(n + 1) is folded to get y(n + 1)

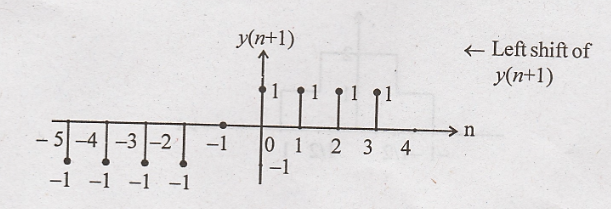
y(n-1) (or) y(-n+1)

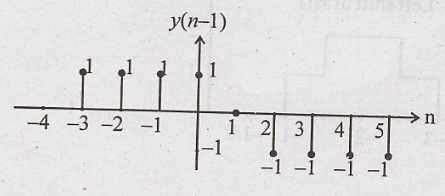
Problem 4:

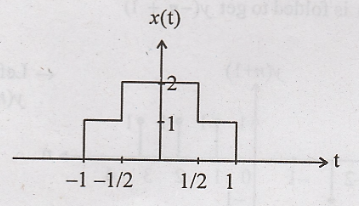
For the x(t), given in figure, obtain

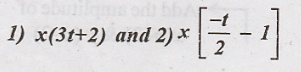 May 2007 - Marks 8

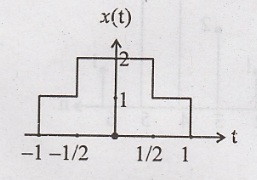
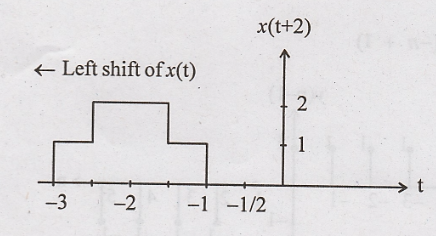
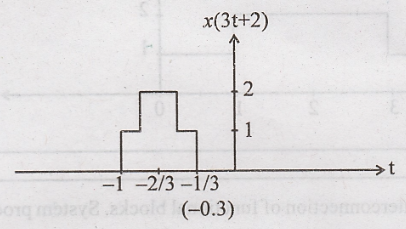
x(3t + 2):

Step 1: Signal x(t) is advanced (left shift) by 2 to get x(t + 2)

Step 2: Signal x(t + 2) is compressed by 3 to get x(3t + 2)

x(t + 2):

x(3t + 2)

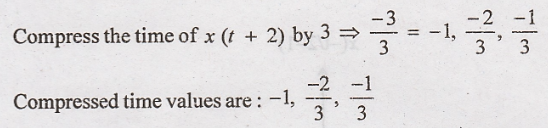
(ii)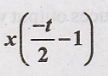 

Step 1: x(t) is delayed by 1 (left shift) to get x(t - 1).

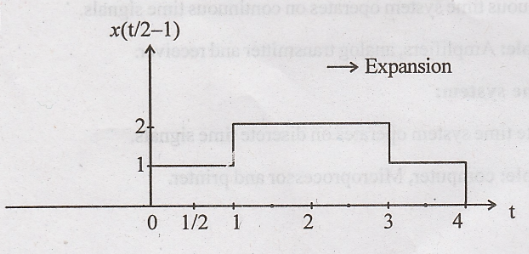
Step 2: x(t - 1) is expanded by 2 to get x(t/2 - 1)

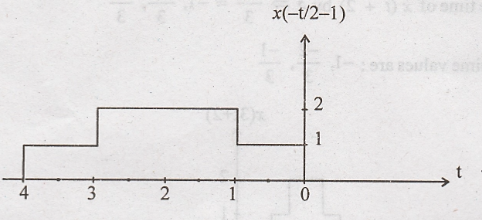
Step 3: x(t/2 - 1) is folded to get x(-t/2 - 1)

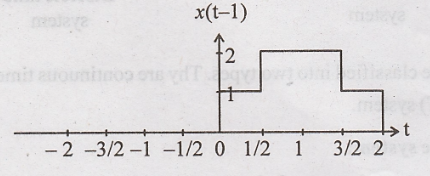
x(t/2 - 1)

x(-t/2 - 1)