Important 2 mark Questions with Answers

TWO MARK QUESTIONS WITH ANSWERS

UNIT 1: CLASSIFICATION OF SIGNAL AND SYSTEM

1. State the properties of an impulse function.

a. Shifting property: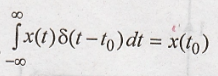 

b. Replication property: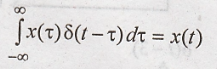 

2. Define signal. What are the classification of signal?

Signal is a function of one (or) more independent variables which contains some information.

Signals are classified as

(i) Periodic and aperiodic signals.

(ii) Energy and power signals.

(iii) Deterministic and random signals.

3. Define energy signal

A signal is said to be energy signal if its normalized energy is finite and nonzero. (0 < E < ∞).

Energy of continuous time signal

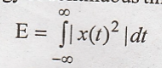
Energy for discrete time signal

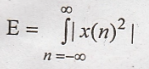
4. Define step function and delta function.

5. Draw the waveform δ(t-3).

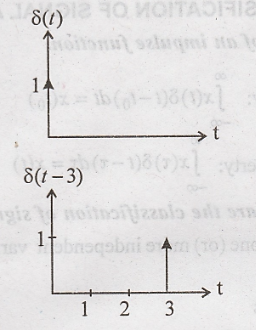
6. What are the classification of systems?

Systems are classified as follows.

a. Static and dynamic system

b. Time variant and time invariant system

c. Linear and non linear system

d. Causal and non causal system.

e. Stable and unstable system.

7. Determine whether the signal x(n) = cos(0.1πn) is periodic or not.

x(n) = cos(0.1πn)

Compare the signal with cos(2π fn)

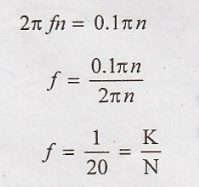
f is rational. Hence the given signal is periodic signal. Fundamental time period N = 20.

8. Calculate the power and RMS value of the signal x(t) = e ^{j α t} cos ω₀t

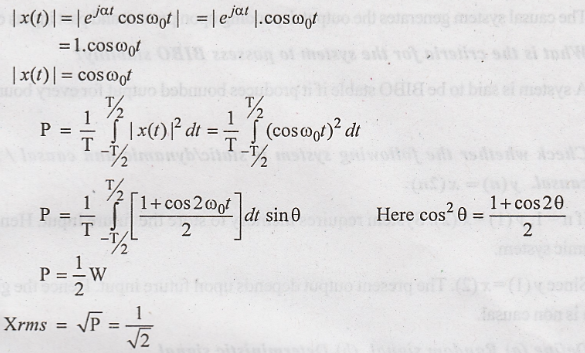
9. What is the periodicity of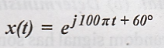 

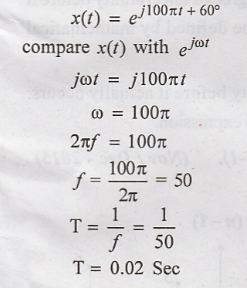
10. Draw the signal u(t-5)

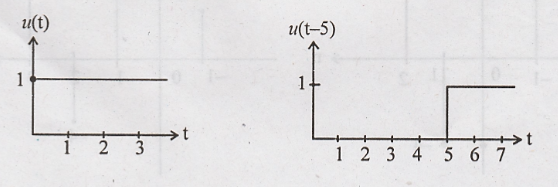
11. Define causal system.

The causal system generates the output depending upon present and past inputs only.

12. What is the criteria for the system to possess BIBO stability?

A system is said to be BIBO stable if it produces bounded output for every bounded input.

13. Check whether the following system is static / dynamic and causal / non causal. y(n) = x(2n).

If n = 1, y(1) = x(2). System requires memory to store the future input. Hence it is dynamic system.

Since y(1) = x(2). The present output depends upon future input. Hence the given system is non causal.

14. Define (a) Random signal. (b) Deterministic signal.

(a) Random signal: A random signal has some degree of uncertainity before it actually occurs. The random signal cannot be defined by mathematical expression.

(b) Deterministic signal: There is no uncertainity before it actually occurs. Deterministic signal is defined by mathematical expression.

15. Given x(n) = {1, 2, 3, -4, 6}. plot the signal x(n-1). (Nov/Dec-2015)

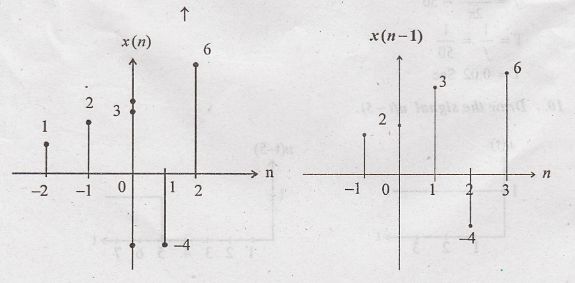
16. State the properties of an inpulse function.

(i) Shifting property :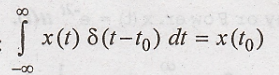 

(ii) Reprication property : 

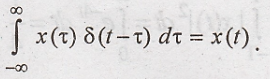
17. Verify whether the system described by the equation y(t) = x(t²) is linear and time invariant.

(i) The system is linear since output is direct function of input.

(ii) The system is time invariant since time parameter is squared in the given system equation.

18. Define the shifting property of the discrete time unit impulse function.

Shifting property is given as

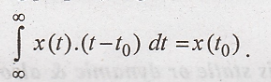
19. Determine whether system y(n) = log(1+|x(n)|) is stable or not.

Here y(n) = log (1+|x(n)|) is taken. This means 1 + |x(n)| > 0. Hence y(n) will be bounded for all bounded values of x(n).

Therefore the system is stable.

20. Calculate the power and RMS value of the signal x(t) = e^{j α t} cos ω₀t.

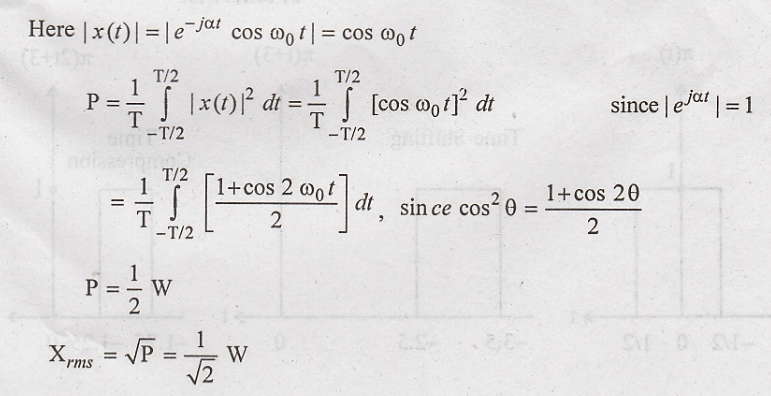
21. Determine whether the following signal is energy or power signal. And Calculate its Energy or Power. x(t) = e ^-2t u(t). [Nov – 12]

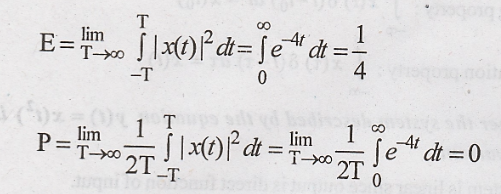
Since Energy is finite & P = 0, x(t) is an Energy signal.

22. What is the condition for stable system?

A LTI system is stable if ∑ |h(n)| < ∞. Here the summation is absolutely summable.

23. Check whether the following system is static or dynamic & also causal or noncausal. y(n) = x(2n). [Nov-12]

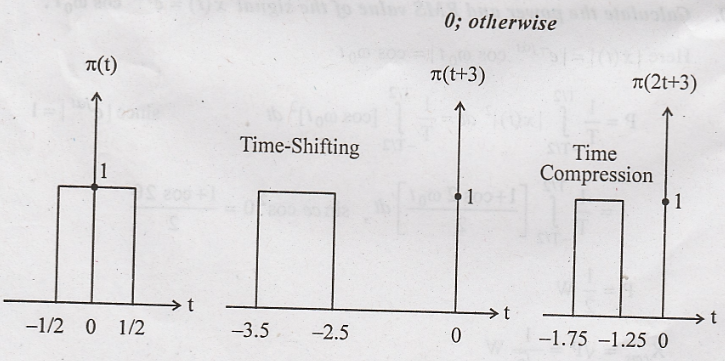
Since the output y(n) depends on the future input, y(n) = x(2n) is a Dynamic system & also a Non-causal system.

24. Draw the function π (2t + 3) when π(t) = 1; for t ≤ 1/2

25. Give the mathematical & graphical representation of CT & DT unit impulse function.

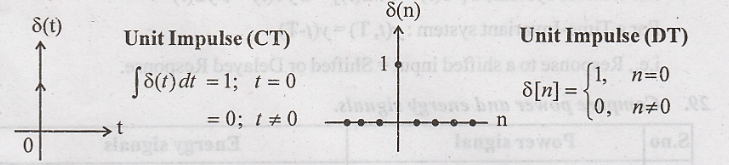
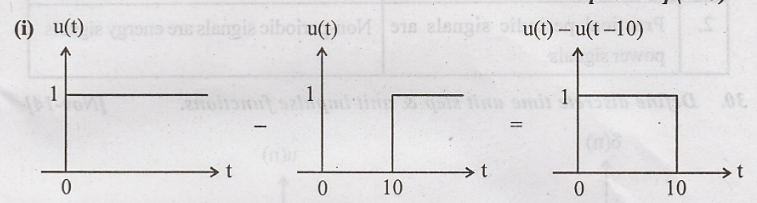
26. Draw the following signals. (i) u(t) - u(t-10) (ii) (1/2)ⁿ u(n-1) [Nov-14] (R13)

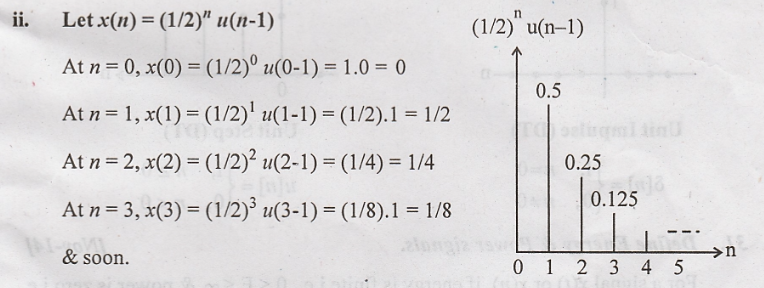
27. Give the relation between continuous time unit impulse function f(t), step function u(t) & ramp function r(t). [Nov-15] (R13)

Continuous-time unit impulse and unit step functions:

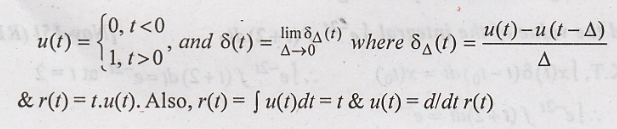
28. What are the conditions for a system to be LTI system?

For a linear system;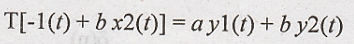 

For a Time-Invariant system: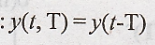 

i.e., Response to a shifted input = Shifted or Delayed Response.

29. Compare power and energy signals.

30. Define discrete time unit step & unit impulse functions.

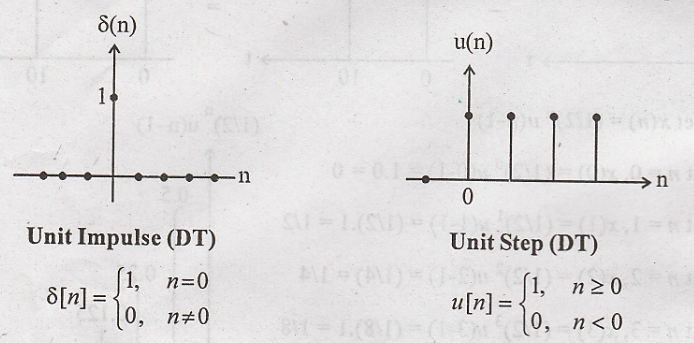
31. Define Energy & Power signals. [Nov-14]

For a signal x(t) or x(n), if energy is finite i.e., 0 < E < ∞ & power is zero i.e., P = 0; then, that signal is called an Energy Signal.

For a signal x(t) or x(n), if power is finite i.e., 0 < P < ∞ & energy is infinite i.e., E = ∞; then, that signal is called an power signal.

32. Find the value of the integral 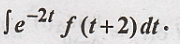 [Nov-15] (R13)

33. State the condition for a signal which is addition of two periodic signal is indicto be periodic.

The sum of two periodic signals is periodic only if the ratio of their respective periods can be expressed as a rational number. Fundamental period is the least common multiple of T1 and T2.

34. Define continuous time system.

A continuous time system is a system in which continuous time input signals are applied and result in continuous time output signals.

35. What is meant by linear system?

A linear system should satisfy superposition principle. A linear system should satisfy 

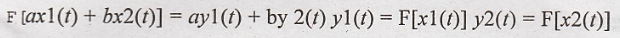
36. What are the basic operations on Signals?

(i) Time shifting

(ii) Time scaling

(iii) Time reversal

(iv) Amplitude scaling

(v) Signal addition

(vi) Signal multiplication

37. Define time invariant system.

A system is time invariant if the behavior and characteristics of the system are fixed over time.

A system is time invariant if a time shift in the input signal results in an identical time shift in the output signal. For example, a time invariant system should produce y(t-10) as the output when x(t-t0) is the input.

38. Define stable system.

When the system produces bounded output for bounded input, then the system is called bounded input & bounded output stable. If the signal is bounded, then its magnitude will always be finite.

39. Define memory and memoryless system.

The output of a memory system at any specified time depends on the inputs at that specified time and at other times. Such systems have memory or energy storage elements. The system is said to be static or memoryless if its output depends upon the present input only.

40. Define invertible system.

A system is said to be invertible if the input is get from the output. Otherwise the system is noninvertible system.

41. What is superposition property?

If an input consists of the weighted sum of several signals, then the output is the Superposition of all the input signals.

42. Define even and odd signal.

Even signal:

a. A discrete time signal is said to be even when, x[-n] = x[n].

b. The continuous time signal is said to be even when, x(-t) = x(t)

c. For example, Cos (on) is an even signal.

Odd signal:

a. The discrete time signal is said to be odd when x[-n] = -x[n]

b. The continuous time signal is said to be odd when x(t) = -x(t)

c. Odd signals are also known as nonsymmetrical signal. Sine wave signal is an odd signal.

43. Define unit pulse function.

Unit pulse function (t) is obtained from unit step signals π(t) = u(t+1/2) - u(t-1/2). The signals u(t+1/2) and u(t-1/2) are the unit step signals shifted by 1/2 units in the time axis towards the left and right, respectively.

44. What is continuous time growing exponential signal?

Continuous time growing exponential signal is defined as x(t) = C e^{a t} where c and a are complex numbers. If 'a' is positive, as t increases, then x(t) is a growing exponential.

45. What is continuous time decaying exponential?

Continuous time growing exponential signal is defined as x(t) = C e^{a t} where c and a are complex numbers. If 'a' is negative, as t increases, then x(t) is a decaying exponential.