Expression for Electrical Conductivity of a Metal (Derivation)

EXPRESSION FOR ELECTRICAL CONDUCTIVITY OF A METAL (Derivation) 

(Based on Drude and Lorentz classical free electron theory)

When an electric field E is applied to an electron of charge 'e' in a metal rod, the electron moves in opposite direction to the applied field with a velocity v_d (Fig. 2.5). This velocity is known as drift velocity.

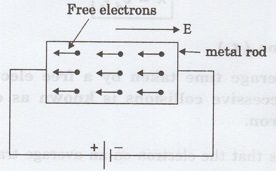
Fig. 2.5 Movement of free electrons in a metal rod

Force experienced by the electron F = e E .................(1)

This force accelerates the electron and hence, it gains acceleration 'a',

From, Newton's second law of motion, the force on the electron

F = Mass of the electron (m) × acceleration (a)

F = ma .................(2)

From the eqns (1) and (2), we have

ma = eE

a = eE / m .................(3)

From equation (3), it is found that the electron should be accelerated continuously due to the applied electric field.

But, the accelerated electron collides with positive ion core and other free electrons. Hence it loses kinetic energy and velocity. Thus, after each collision, the velocity of electron increases until the next collision takes place.

Average drift velocity of electron is = v_d

If τ_c is collision time, then acceleration.

a = v_d / τ (`.`τc = τ)

v_d = a τ .................(4)

Substituting the eqn (3) in (4)

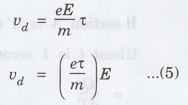
But, the current density in terms of drift velocity is given as

J = n e v_d .................(6)

Substituting the eqn (5) in (6), we have

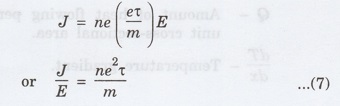
According to Ohm's law, current density (J) is expressed as

J = σ E or σ = J / E .................(8)

On comparing the eqns (7) and (8), we have

Electrical conductivity σ = n e² τ / m .................(9)

The eqn (9) represents electrical conductivity of the metal

Thermal Conductivity (K)

We know that the amount of heat conducted between the two ends of a metal rod.

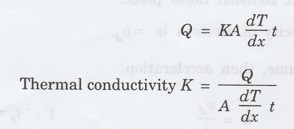
It is defined as the amount of heat conducted per unit time through the material having unit area of cross-section per unit temperature gradient.

If area of cross section A is '1' m².

time of flow of heat t is 1 second, then

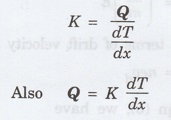
Q - Amount of heat flowing per unit time through unit cross-sectional area.

dT/dx - Temperature gradient.