Examples on Stable and Unstable System

Examples on stable and unstable system

Determine whether the following systems are stable (or) unstable.

1. y(t) = x(-t)

Solution:

As long as x(t) is bounded, y(t) also bouned. Hence the given system is stable.

2. T[x(n)] = a x(n) + b

Solution:

T[x(n)] = y(n)

Since y(n) is bounded as long as x(n) is bounded, given system is stable.

3. y(t) = cos[x(t)]

Solution:

Maximum and minimum value of cosine function is +1 and -1. Hence output y(t) is bounded for bounded input and the given system is stable.

4. y(t) = e ^{t x(t)}

Solution:

For bounded input, y(t) → ∞ as t → ∞. Hence the given system is unstable.

5. y(n) = n x(n)

Solution:

For bounded input, y(n) → ∞ as n → ∞. Hence the given system is unstable.

6. y(t) = x(t) cos 100 πt

Solution:

As long as input x(t) is bounded, y(t) also bounded. Hence the given system is stable.

7. y(n) = x(n) + nx(n+1)

Solution:

For bounded input y(n) → ∞ as n → ∞. Output is unbounded for bounded input. Hence the given system is unstable.

8. y(t) = x(-t)

Solution:

As long as x(t) is bounded, y(t) is bounded. Hence the given system is stable.

9. y(t) = x(t + 10) + x²(t)

Solution:

Since y(t) is bounded as long as x(t) is bounded, given is stable.

10. y(t) = 10 x(t) + 5

Solution:

Since y(t) is bounded as long as x(t) is bounded, given system is stable.

11. y(n) = sin [x(n)] / x(n)

Solution:

When x(n) → 0, y(n) = sin 0 / 0 = 1, by L Hospitals rule. Hence the given system is stable.

12. y(n) = x(n)

Solution:

Since y(n) is bounded as long as x(n) is bounded, given system is stable.

13. y(n) = |x(n)|

Solution:

As long as x(n) is bounded, its magnitude and y(n) is bounded. Hence the given system is stable.

14. y(n) = log₁₀x(n)

Solution:

If x(n) = 0, y(n) = ∞. When x(n) is bounded y(n) is unbounded. Hence the given system is unstable.

15. T[x(n)] = e^x(n)

Solution:

T[x(n)] = y(n)

As long as x(n) is bounded y(n) also bounded. Hence the given system is stable.

16. y(n) = ax(n)

Solution:

As long as x(n) is bounded y(n) also bounded. Hence the given system is stable.

17. y(n) = x(n) u(n)

Solution:

As long as x(n) is bounded y(n) also bounded. Hence the given system is stable.

18. y(t) = x(t) cos(100 πt)

Solution:

Maximum value of cosine function is 1. Bounded value of x(t) produces bounded output. Hence the given system is stable.

19. 

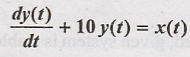
Solution:

As long as x(t) is bounded, y(t) is bounded. Hence the given system is stable.

20. y(n) = 2x(2ⁿ)

Solution :

Output is double for any bounded input. Hence the given system is stable.

21. 

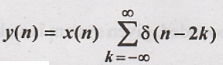
Solution:

As long as x(n) is bounded, y(n) is bounded. Hence the given system is stable.

22. y(n) = sgn[x(n)]

Solution:

Since y(n) is bounded as long as x(n) is bounded, given system is stable.

23. y(t) = x(t²)

Solution:

As long as x(t) is bounded, y(t) also bounded. Hence the given system is stable.