Examples on Linear (or) Non Linear System

Examples on Linear (or) Non Linear System 

Determine whether the following systems are linear (or) non linear.

1. y(t) = x(3-t)

Solution:

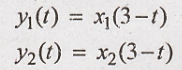
Condition for linear system.

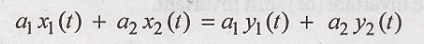
L.H.S

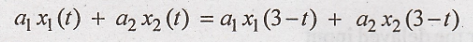
R.H.S

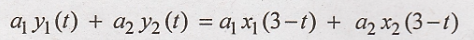
L.H.S = R.H.S

Hence the given system is linear.

2. y(t) = x²(t)

Solution

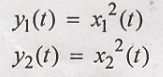
Condition for linear system

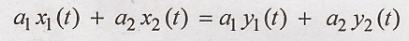
L.H.S

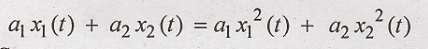
R.H.S

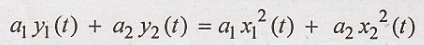
L.H.S. = R.H.S

Hence the given system is linear.

3. y(t) = 5x(t) + 3

Solution

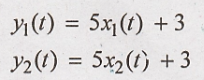
Condition for linear system.

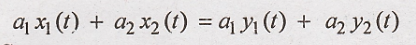
L.H.S.

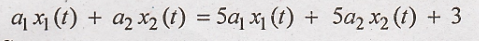
R.H.S

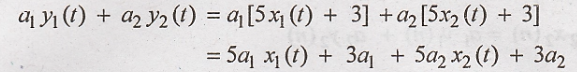
L.H.S ≠ R.H.S

Hence the given system is non linear system

4. y(t) = x(t) cos 50πt

Solution

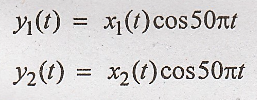
Condition for linear system

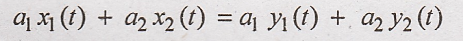
L.H.S

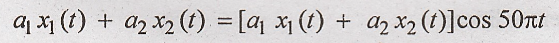
R.H.S

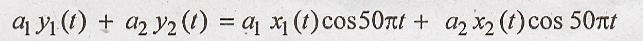
L.H.S = R.H.S

Hence the given system is linear.

5. y(n) = cos[x(n)]

Solution:

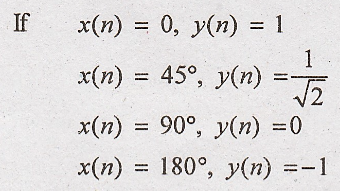
when x(n) increases, y(n) decreases. Hence the given system is non linear system.

6. y(n) = x(-2n)

Solution

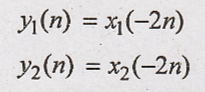
Condition for linear system

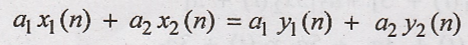
L.H.S

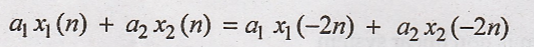
R.H.S

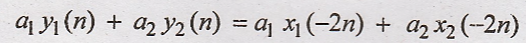
L.H.S = R.H.S

Hence the given system is linear system.

7. 

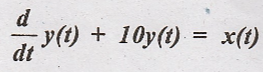
Solution:

This is linear differential equation.

Hence the given system is linear.

8. y(n) = log₁₀(|x(n)|)

Solution:

Logarithmic function is nonlinear. Hence the given system is non linear.

9. 

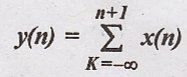
Solution:

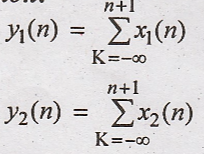
Condition for linear system.

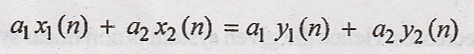
L.H.S

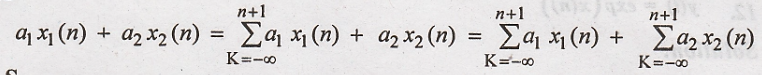
R.H.S

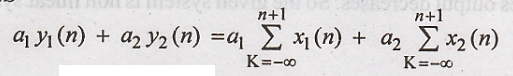
Hence the given system is linear.

10. y(t) = x(2-t)

Solution:

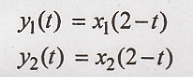
Condition for linear system.

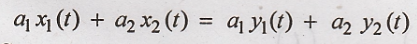
L.H.S

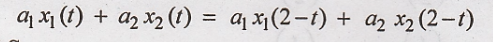
R.H.S.

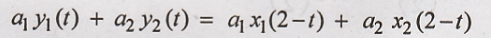
L.H.S = R.H.S

Hence the given system is linear system.

11. y(n) = x(n) + nx(n+1)

Solution:

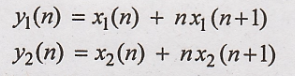
Condition for linear system.

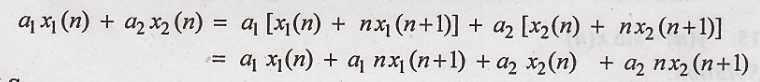
R.H.S

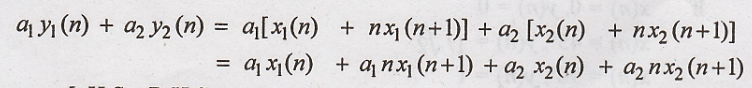
L.H.S = R.H.S

Hence the given system is linear system.

12. y(t) = exp(x(n))

Solution:

When input increases output decreases. So the given system is non linear system.

13. y(t) = x (t/2)

Solution:

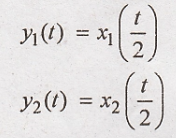
Condition for linear system:

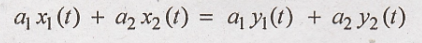
L.H.S.

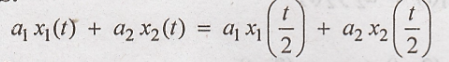
R.H.S

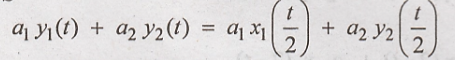
L.H.S = R.H.S

Hence the given system is linear system.

14. y(t) = cos [x(t)]

Solution:

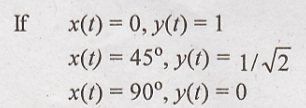
when x(t) increases, y(t) decreases. Hence the given system is non linear system.

15. y(n) = sin x(n)

Solution:

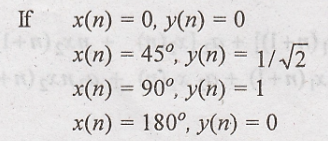
When x(n) increases, first y(n) increases and decreases. Hence the given system is non linear system.

16. 

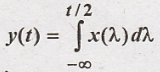
Solution:

Since integration operation is linear, given system is linear system.

17. y(n) = |x(n)|

Solution:

Magnitude operation is non linear. Hence the given system is non linear.

18. 

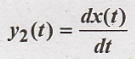
Solution:

Since differentiation operation is linear, given system is linear.

19. y(n) = x(n) cos(ω₀n)

Solution:

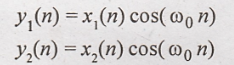
condition for linear system

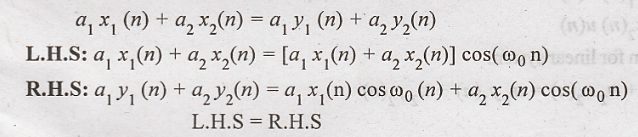
Hence the given system is linear.

20. y(n) = nx(n)

Solution:

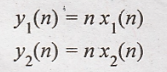
condition for linear system

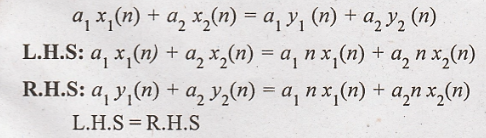
Hence the given system is linear system.

21. y(n) = ax(n)

Solution:

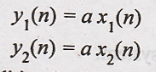
Condition for linear system

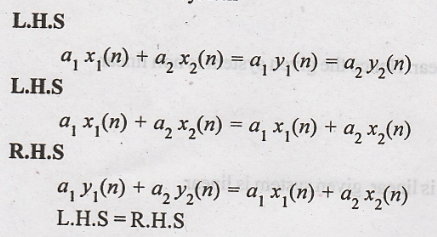
Hence the given system is linear.

22. y(n) = x(n) u(n)

Solution:

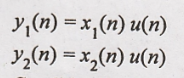
Condition for linear system

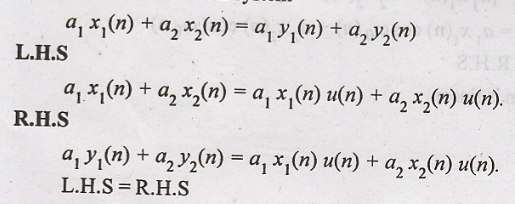
Hence the given system is linear.

23. y(t) = x(5-t)

Solution:

 

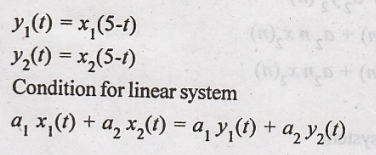
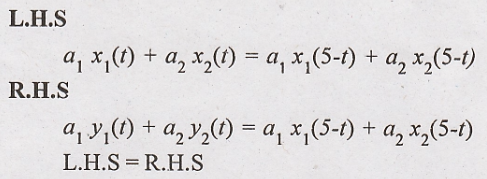
Hence the given system is linear

24. y(t) = x(t²)

Solution:

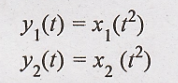
Condition for linear system

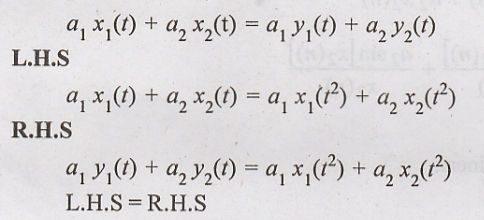
Hence the given system is linear.

25. T[x(n)] = ax(n) + b

Solution:

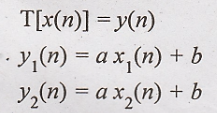
Condition for linear system

Hence the given system is non linear.

26. 

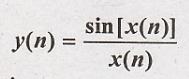
Solution :

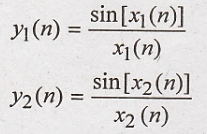
Condition for linear system.

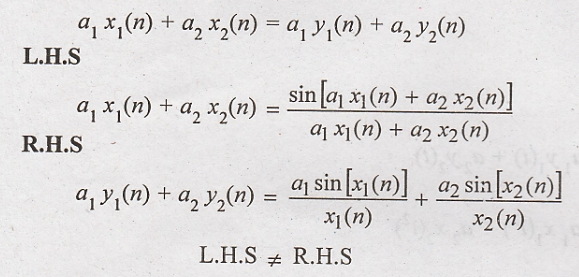
Hence the given system is non linear.

27. y(n) = cos [2πx(n+1)] + x(n)

Solution:

Cosine term makes the system nonlinear.

28. y(n) = x(-n)

Solution:

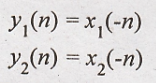
Condition for linear system

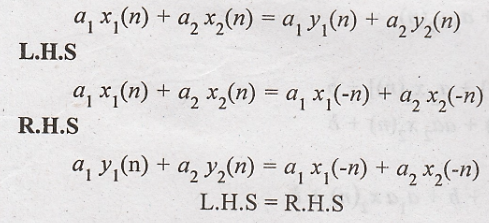
Hence the given system is linear.