Examples on Causal and Non Causal System

Examples on Causal / Non Causal System

Determine whether the following continuous time systems are causal or non causal.

1. y(t) = e^x(t)

Solution:

Output y(t) depends upon the present input x(t). Hence this is causal system.

2. y(t) = x(t+10) + x²(t)

Solution:

Output y(t) depends upon the future input x(t+10). Hence this is non causal system.

3. 

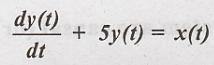
Solution:

Output y(t) depends upon the present input x(t). Hence this is causal system.

4. y(t) = x(t) cos (50 πt)

Solution:

Output y(t) depends upon the present input x(t). Hence this is causal system.

5. y(t) = x(t-2) + x(2−t)

Solution:

x(t-2) is past input, but x(2-t) is future input. Hence this is non causal system. [Hint: x(2-t) can be written as x(-t+2)].

6. y(t) = cos[x(t)]

Solution:

Output y(t) depends upon present input x(t). Hence the given system is causal system.

7. y(t) = x(t/4)

Solution:

If t = -8, y(-8) = x(-2). x(-2) is future input. Hence the given system is non causal system.

8. 

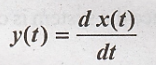
Solution:

Differentiation of present input leads to past input. Output y(t) depends upon past input. Hence the given system is causal system.

9. y(t) = x(t) cos 100лt

Solution:

Output y(t) depends upon present input x(t). Hence the given system is causal system.

10. 

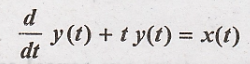
Solution:

Output y(t) depends upon present input x(t). Hence the given system is causal.

11. y(t) = x(t + 10) + x²(t)

Solution:

Output y(t) depends upon future input x(t+10). Hence the given system is non causal.

12. y(t) = e ^{t x(t)}

Solution:

Output y(t) depends upon present input x(t). Hence the given system is causal system.

Determine whether the following discrete time system are causal (or) non causal.

1. y(n) = |x(n)|

Solution:

Output y(n) depends upon the present input x(n). Hence the system is causal.

2. 

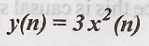
Solution:

Output y(n) depends upon the present input x(n). Hence the given system is causal.

3. y(n) = sin [3πx(n+1)]

Solution:

Output y(n) depends upon the future input x(n+1). Hence the system is noncausal.

4. y(n) = x(4n)

Solution:

Output y(n) depends upon the future input. Hence the system is noncausal. [Hint: When n= 1, y(1) = x(4) → future input.]

5. y(n) = x(n) sin(ω₀n)

Solution:

Output y(n) depends upon the present input x(n). Hence the system is causal.

6. y(n) = x(3-n)

Solution:

x(3-n) can be written as x(-n+3). Output depends upon the future input x(3-n). Hence the system is noncausal.

7. y(n) = sin [x(n)]

Solution:

Output y(n) depends upon present input x(n). Hence the given system is causal system.

8. 

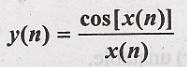
Solution:

Output y(n) depends upon present input x(n). Hence the given system is causal.

9. 

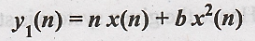
Solution:

Output y₁(n) depends upon present input x(n). Hence the given system is causal.

10. y(n) = log₁₀(|x(n)|)

Solution:

Output depends upon present input x(n). Hence the given system is causal.

11. y(n) = x(n) u(n)

Solution:

Output depends upon present input x(n). Hence the given system is causal.

12. y(n) = sgn[x(n)]

Solution:

Output depends upon present input x(n). Hence the given system is causal.

13. T[x(n)] = ax(n) + b

Solution:

T[x(n)] means output y(n). Output y(n) depends upon input x(n). Hence the given system is causal.

14. y(n) = x(2n)

Solution:

Example: If n = 2, y(2) = x(4)

Output y(n) depends upon future input. Hence the given system is noncausal system.

15. y(n) = n x(n)

Solution:

Output y(n) depends upon present input x(n). Hence the given system is causal system.

16. y₁(n) = e ^x(n)

Solution:

Output y₁(n) depends upon present input x(n). Hence the given system is causal system.

17. y₁(n) = x(n) + x(n+1)

Solution:

Output y₁(n) depends upon present input x(n) and future input x(n+1). Hence the given system is noncausal.

18. y(n) = e ^{n x(n)}

Solution:

Output y(n) depends upon present input x(n). Hence the given system is causal system.