Examples Based on Time Variant and Time Invariant System

Examples Based on Time Variant / Time Invariant System

1. y(t) = sin x(t)

Output of the system for the delayed input

Hence the system is time invariant.

2. y(t) = t x(t)

Output of the system for the delayed input is given by

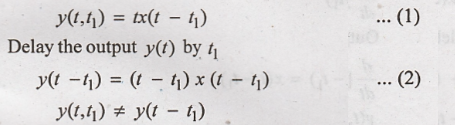
Hence the given system is time variant.

3. y(t) = x(t) cos 200πt

Output of the system for the delayed input is given by

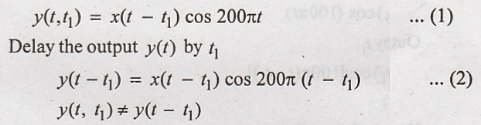
Hence the given system is time variant.

4. y(t) = x(t) cos (t + 1)

Output of the system for the delayed input is given by

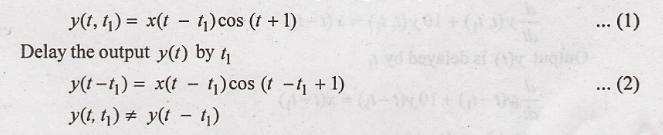
Hence the given system is time invariant.

5. y(t) = 10x(t) + 5

Output y(t) for the delayed input.

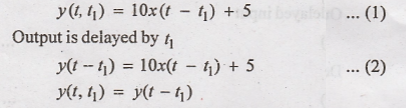
Hence the given system is time invariant.

6. 

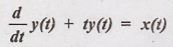
Output y(t) for the delayed input is given by

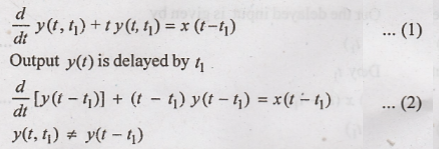
Hence the given system is time variant. it a

7. y(t) = x(t) cos (100πt)

Output y(t) for the delayed input is given by

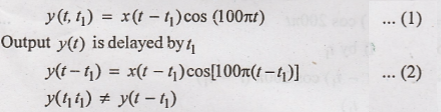
Hencme the given system is time variant

8. 

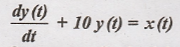
Output y(t) for the delayed input

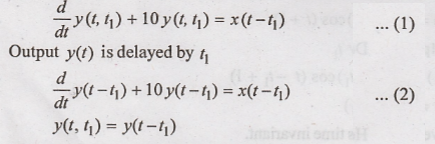
Hence the given system is time invariant.

9. y(t) = x(t+10) + x²(t)

Output y(t) for the delayed input is given by.

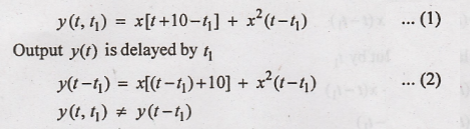
Hence the given system is time variant.

10. y(t) = x(t²)

Output y(t) for delayed input is given by

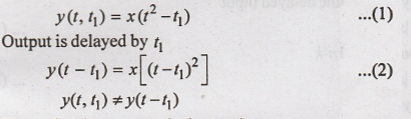
Hence the given system is time variant

11. y(t) = e ^x(t)

Output y(t) for the delayed input is given by

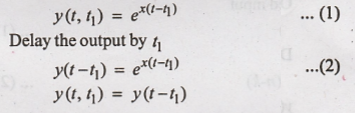
Hence the given system is time invariant

12. y(t) = x(t−2) + x(2-t)

Output y(t) for the delayed input is given by

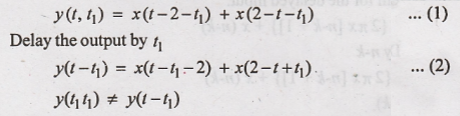
Hence the given system is time variant.

13. 

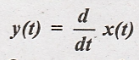
Output y(t) for the delayed input is given by

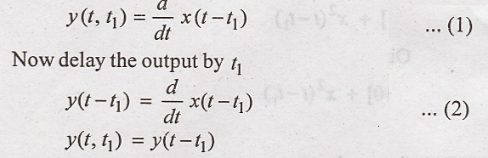
Hence the given system is time invariant.

14. y(n) = |x(n)|

Solution:

Output of the system for the delayed input

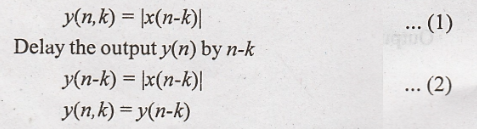
Hence the system is time invariant (or) shift invariant.

15. y(n) = n x(n) + b x²(n)

Solution:

Output of the system for the delayed input

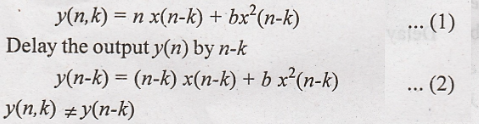
Hence the given system is time variant (or) shift variant.

16. y(n) = cos [2πx (n+1)] + x(n)

Solution:

Output of the system for the delayed input.

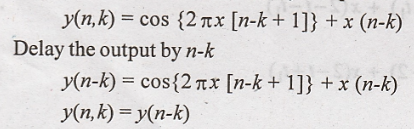
Hence the given system is time invariant (or) shift invariant.

17. y(n) = log₁₀(|x(n)|)

Solution:

Output of the system for the delayed input

Hence the given system is time invariant (or) shift invariant.

18. y(n) = x(n) + nx(n+1)

Solution:

Output of the system for the delayed input

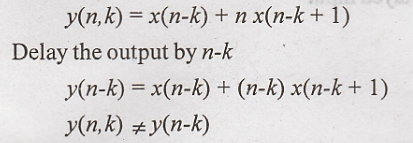
Hence the given system is time variant (or) shift variant.

19. y(n) = x(2n)

Solution:

Output of the system for the delayed input

Hence the given system is time variant (or) shift variant.

20. y(n) e^x(n)

Solution:

Output of the system for the delayed input

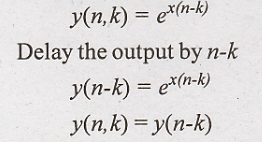
Hence the given system is time invariant

21. y(n) = n x(n)

Solution:

Output of the system for the delayed input

Hence the given system is time invariant.

22. y(n) = ax(n)

Solution:

Output of the system for the delayed input

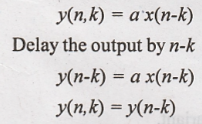
Hence the given system is time invariant.

23. y(n) = x(n) u(n)

Solution:

Output of the system for the delayed input

y(n,k) = x(n-k) u(n)

Delay the output by n-k

y(n-k) = x(n-k) u(n-k)

Hence the given system is time invariant

24. y(n) = x(n) cos (ω₀n)

Solution:

Output of the system for the delayed input

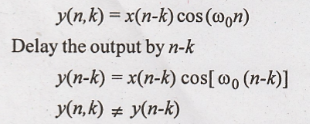
Hence the given system is time variant (or) shift variant.

25. y(n) = ax(n) + b

Solution:

Output of the system for the delayed input.

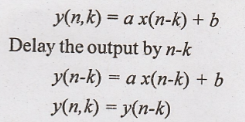
Hence the given system is time invariant (or) shift invariant.

26. y(n) = x(-n)

Solution:

Output of the system for the delayed input

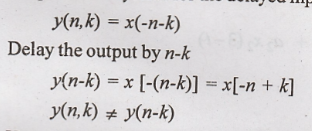
Hence the given system is time variant (or) shift variant.

27. y(n) = sin [x(n)]

Solution:

Output of the system for the delayed input

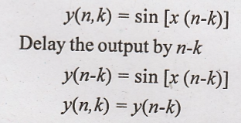
Hence the given system is time invariant (or) shift invariant.

28. y(n) = 2x(2ⁿ)

Solution:

Output of the system for the delayed input

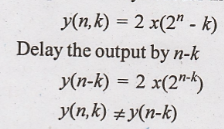
Hence the given system is time variant (or) shift variant.