Energy and Power Signals

Energy and Power Signals

Energy signal:

Continuous time signal x(t) is said to be energy signal if the total normalized energy of the signal is finite and non zero.

0 < E < ∞

E---> Energy of the signal.

Total normalized energy:

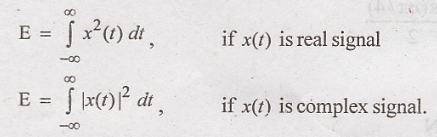
Discrete time signal x(n) is called energy signal if its energy is finite.

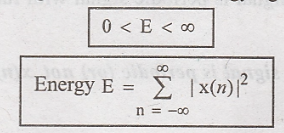
Power signals:

Continuous time signal x(t) is said to be power signal if the normalized average power p is finite and non zero.

0 < P < ∞

Average normalized power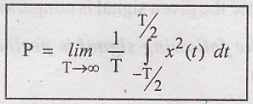 

Discrete time signal x(n) is said to be power signal if its power is finite

0 < P < ∞

Average power of the discrete time signal x(n)

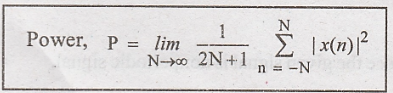
Comparison of energy and power signals :

Problems Based on Energy and Power Signals

1. Determine energy of the discrete time signal.

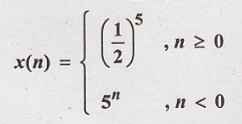
Solution:

Energy of discrete time signal is given by

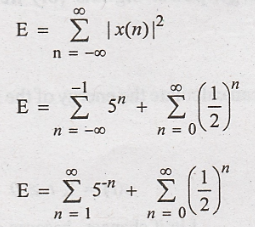
5-n can be written as

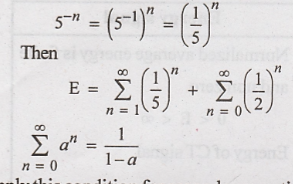
(Apply this condition for second summation term)

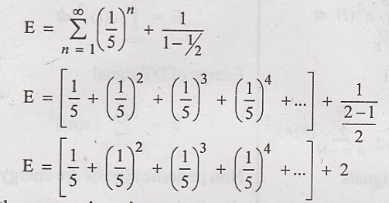
By using the geometric series,

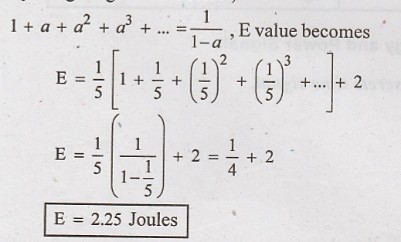
(2) Classify the following signals as energy, power signals (or) neither and find the corresponding value.

(i) x(t) = e – a t u(t), a < 0

This signal is non periodic signal. so we can calculate the energy of the signal.

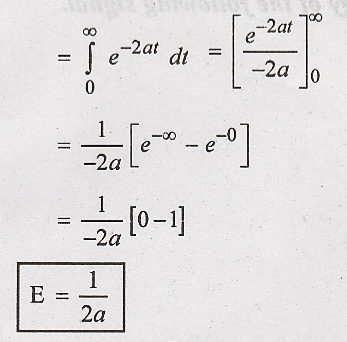
(ii)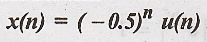 

First we will check the periodicity of the signal

This is non periodic signal with infinite duration. So this is energy signal.

Energy of the signal

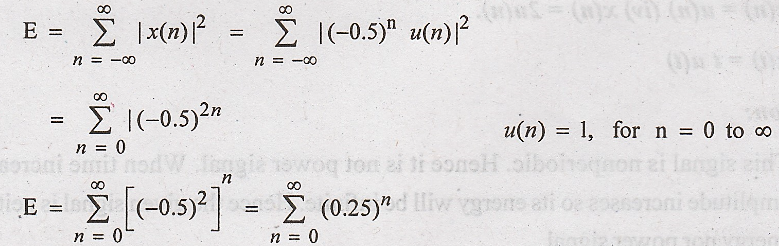
Hence let us use trigonometric series

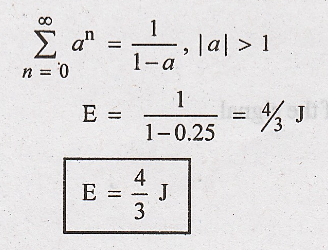
3. Determine the value of power and energy of the following signal.

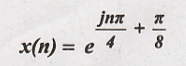
Solution : 

Power of discrete time signal

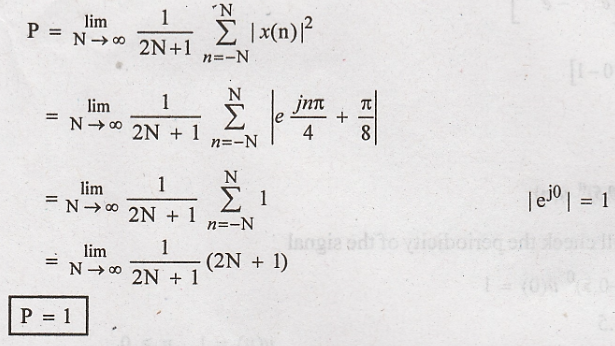
Power of discrete time signal is finite and non zero. Since power is finite and non zero energy is infinite.

4. Classify the following signals as energy, power signals (or) neither and find the corresponding value. 

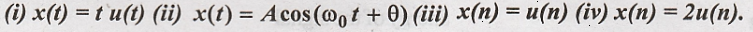
(i) x(t) = t u(t)

Solution:

(i) This signal is nonperiodic. Hence it is not power signal. When time increases amplitude increases so its energy will be infinite. Hence the given signal is neither energy nor power signal.

(ii)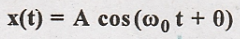 

Solution:

This signal is periodic so, we can calculate power of the signal.

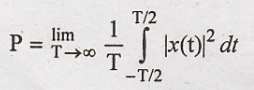
Integration of cosine wave over full cycle is zero. Hence the second term is zero.

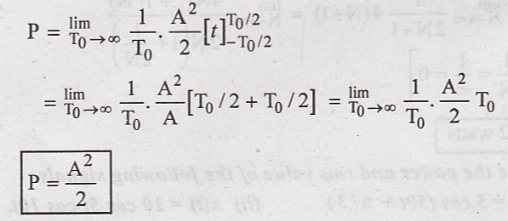
(iii) x(n) = u(n)

Solution:

Unit step signal u(n) is periodic signal with infinite duration. Hence this is power signal.

Power of u(n) is given as

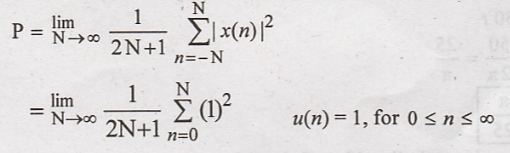
Summation of 1 is written as

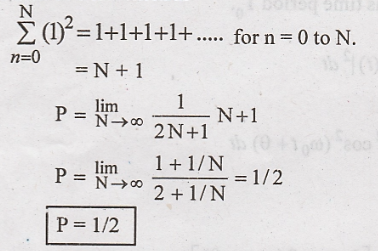
Power is finite and non zero. Hence unit step signal is power signal with P = 1/2.

(iv) x(n) = 2 u(n)

Solution:

Unit step signal u(n) is periodic signal with infinite duration. Hence this is power signal power of 2u(n) is given as

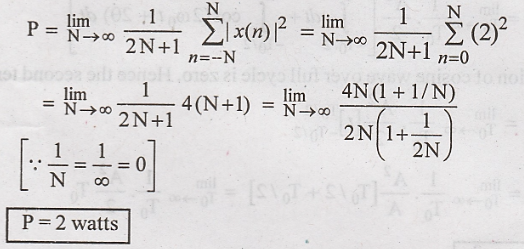
5. Determine the power and rms value of the following signals.

(i) x(t) = 5 cos (50t + π/3)

(ii) x(t) = 10 cos 5t cos 10t.

Solution:

(i) x(t) = 5 cos (50 + π/3)

To obtain fundamental period

compare the given signal with x(t) = A cos (2πft + π/3)

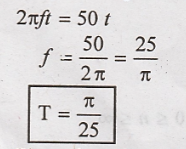
Given signal is periodic with period π/25.

Power :

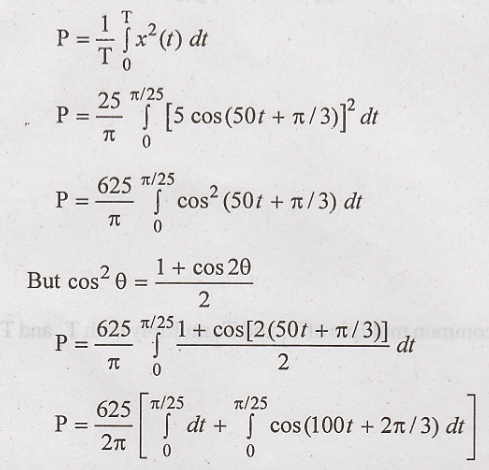
Cosine wave term is zero when it is integrated over full cycle.

(ii) x(t) = 10 cos 5t cos 10t

Solution :

Fundamental period

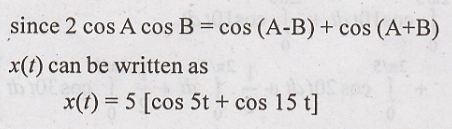
Compare above equation with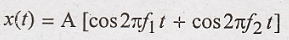 

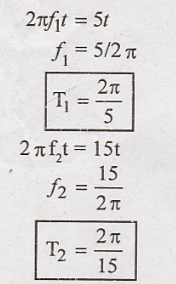
The period will be least common multiple of T1 and T2 multiply both T1 and T2 by 15, we get.

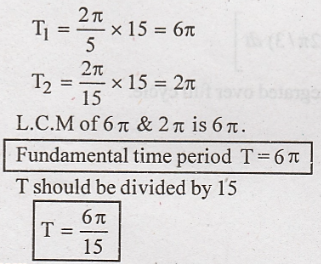
Power:

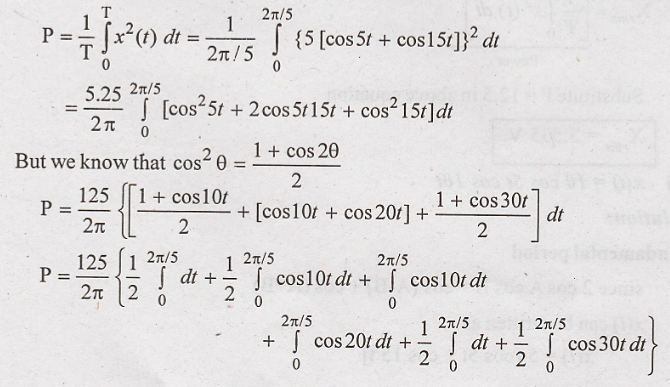
In the above equation, cosine term integrated over full cycle is zero.

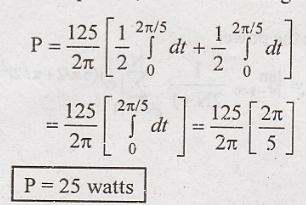
RMS value

RMS value is given as

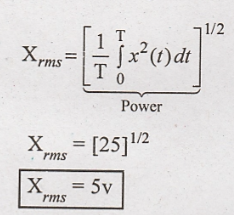
6. Determine whether the following signals are energy (or) power signal. Obtain energy (or) power of the same.

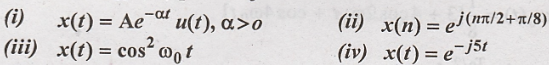
Solution:

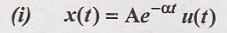
Since the given signal is non periodic signal, energy is calculated.

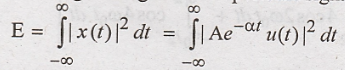
Since u(t) = 1, for 0 ≤ t ≤ ∞, limit changes from 0 to ∞.

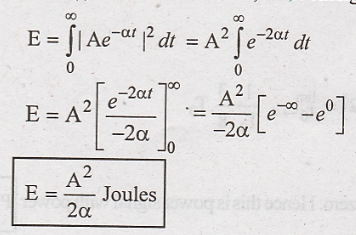
(ii)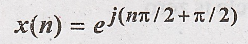 

This is periodic signal. Let us calculate the power

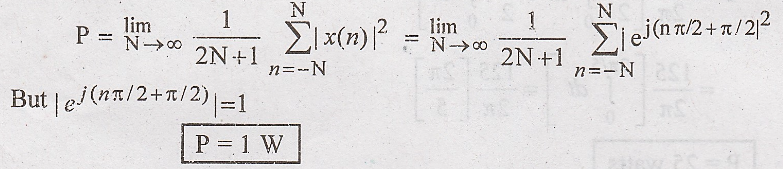
(iii)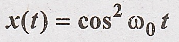 

This is squared cosine wave. Hence this is periodic signal. We must calculate the power.

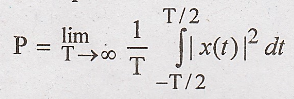
Given signal fundamental time period is T0

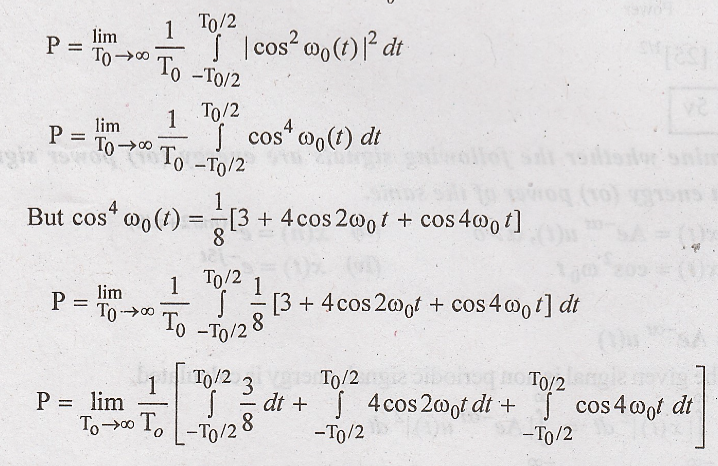
In the above equation, integration of cosine term over a full cycle is zero.

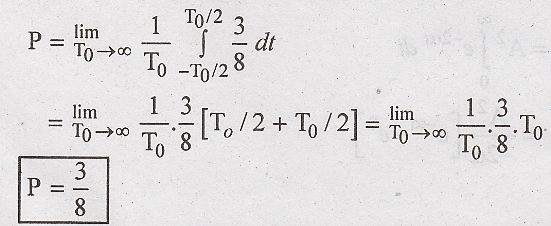
Power of the signal is finite and non zero. Hence this is power signal with power P = 3/8

(iv) x(t) = 6 e – j 5 t

Solution:

Since this is periodic phasor. Let us calculate the power

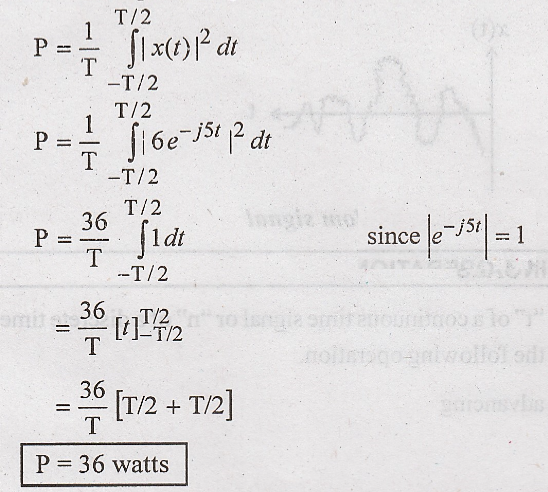
Deterministic and Random Signal

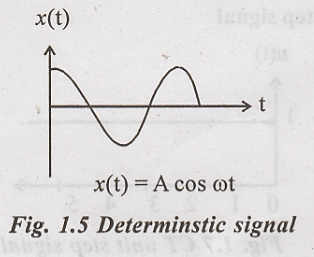
Deterministic signal:

A signal is said to be deterministic signal if it is completely represented by mathematical equation at any time.

Example:

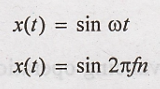
Sine wave, Square wave, Triangular wave, Exponential pulse etc...

Random signal:

Random signal cannot be represented by mathematical equation.

Example:

Noise signal.