Electrical and Instrumentation Engineering: Unit I: Transformer
EMF Equation of a Transformer
Derivation
Voltage applied to primary is alternating in nature, so the flux established also alternating one.
EMF EQUATION OF A TRANSFORMER
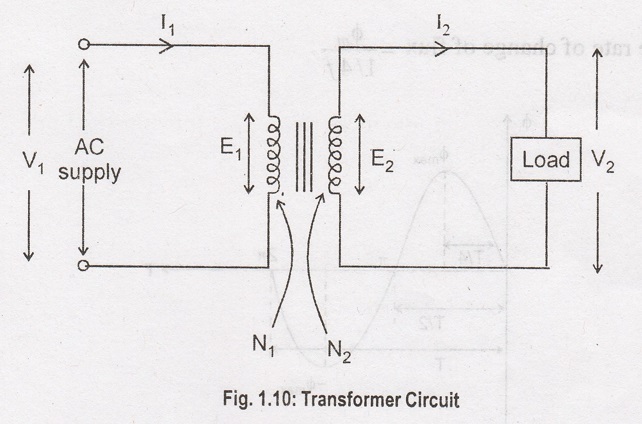
Assume a
transformer arrangement as shown in Figure 1.10:
N1 -
No. of turns in primary winding
N2 -
No. of turns in secondary winding
Φm -
Maximum flux in core in Wb.; where φm = Bm*A
Bm -
Maximum flux density in the core, Wb/m2
A - Area of the
core in m2
f - Frequency of
AC supply in Hz
V1 -
Primary voltage in volts
V2 -
Secondary voltage in volts
I1 -
Full load primary current in amperes
I2 -
Full load secondary current in amperes
E1 -
Emf induced in primary in volts
E2 -
Emf induced in secondary in volts
Voltage applied
to primary is alternating in nature, so the flux established also alternating
one.
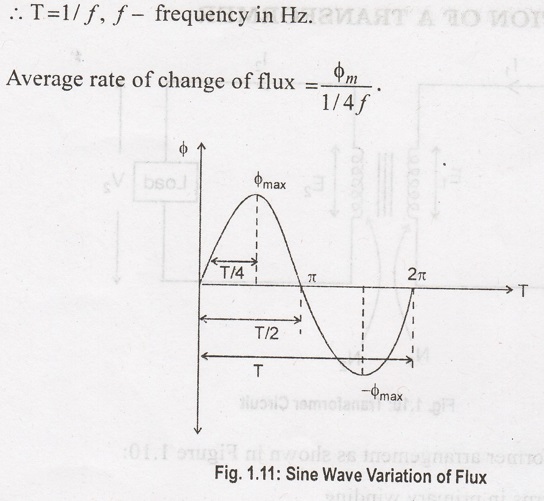
From the Figure
1.11 it is clear that the flux is attaining its maximum value in one quarter of
the cycle. i.e., T/4 sec. where 'T' is the time period in seconds.
If we assume
single turn coil, then according to Faraday's laws of electromagnetic
induction,
Electrical and Instrumentation Engineering: Unit I: Transformer : Tag: : Derivation - EMF Equation of a Transformer
Electrical and Instrumentation Engineering: Unit I: Transformer
Under Subject
Electrical and Instrumentation Engineering
BE3254 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Related Subjects
Professional English II
HS3251 2nd Semester 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Statistics and Numerical Methods
MA3251 2nd Semester 2021 Regulation M2 Engineering Mathematics 2 | 2nd Semester Common to all Dept 2021 Regulation
Engineering Graphics
GE3251 eg 2nd semester | 2021 Regulation | 2nd Semester Common to all Dept 2021 Regulation
Physics for Electrical Engineering
PH3202 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Basic Civil and Mechanical Engineering
BE3255 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Electric Circuit Analysis
EE3251 2nd Semester 2021 Regulation | 2nd Semester EEE Dept 2021 Regulation
Physics for Electronics Engineering
PH3254 - Physics II - 2nd Semester - ECE Department - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Electrical and Instrumentation Engineering
BE3254 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Circuit Analysis
EC3251 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
Materials Science
PH3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd semester Mechanical Dept | 2021 Regulation | 2nd Semester Mechanical Dept 2021 Regulation
Physics for Civil Engineering
PH3201 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Basic Electrical, Electronics and Instrumentation Engineering
BE3252 2021 Regulation | 2nd Semester Civil Dept 2021 Regulation
Physics for Information Science
PH3256 2nd Semester CSE Dept | 2021 Regulation | 2nd Semester CSE Dept 2021 Regulation
Basic Electrical and Electronics Engineering
BE3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation
Programming in C
CS3251 2nd Semester CSE Dept 2021 | Regulation | 2nd Semester CSE Dept 2021 Regulation