Distance Between Successive Planes

DISTANCE BETWEEN SUCCESSIVE PLANES

Interplanar Distances - 'd' Spacing in Cubic Lattice [Derivation]

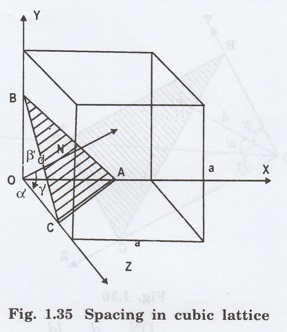
Consider a plane ABC in cubic crystal with a as length of the cube edge as shown in figure 1.35. This plane is one of the plane of the family of planes whose Miller indices are (h k l).

A normal ON is drawn to the plane ABC from the origin of the cube. Let ON be interplanar spacing (d) of this plane.

[Assume that the origin is lying on the plane immediately next to the plane under consideration.]

This plane ABC makes the intercepts OA, OB and OC on the reference axes OX, OY and OZ. α', β' and γ' are the angles between reference axes OX, OY, OZ and the normal ON respectively.

We know that Miller indices of a plane are the smallest integers of the reciprocals of their intercepts. But here, the

intercepts are expressed as reciprocals of Miller indices of the plane.

ie, OA : OB : OC = 1/h : 1/k : 1/l .......................(1)

Multiplying by lattice constant a, we have

OA : OB : OC = a/h : a/k : a/l .......................(2)

OA = a/h , OB = a/k and OC = a/l .......................(3)

From the geometry of right angles OAN, OBN and OCN (Fig 1.36), we have,

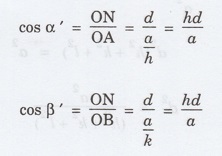
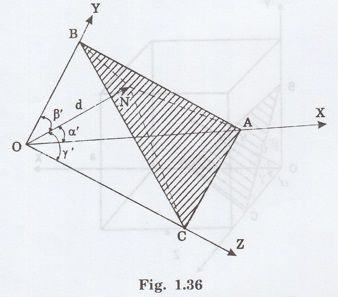
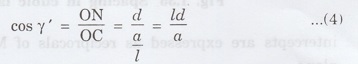
The law of direction cosines is

Substituting for cos α' , cos β' , cos γ' we have,

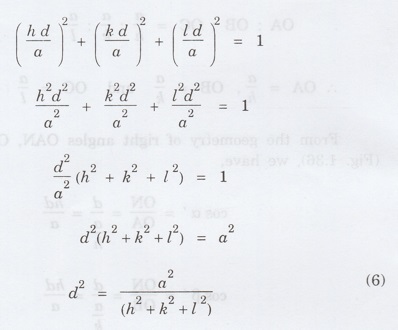
Taking square root on both sides, we have

The above equation gives relation between interplanar spacing d, cube edge a and Miller indices

(h k l).

ANNA UNIVERSITY SOLVED PROBLEMS

Problem 1.5

The lattice constant for a unit cell of aluminium is 4.049 Å. Calculate the spacing of (220) plane. (A.U. Dec 2012)

Given data

a = 4.049 Å

h = 2, k = 2, l = 0

Solution:

We know that d =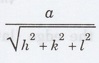 

Substituting the given values, we have

Important Features of Milliner Indices

1. A plane which is parallel to any one of the co-ordinate axes has an intercept of infinity (∞) and therefore, the Miller index for that axes is zero.

2. All equally spaced parallel planes with a particular orientation have index number (h, k, l).

3. Miller indices do not only define a particular plane but a set of parallel plane.

4. It is the ratio of indices which is only of importance. The planes (211) and (422) are the same.

5. A plane passing through the origin is defined in terms of a parallel plane having non-zero intercepts.

Some of the desirable features of Miller index notation are:

(i) The angle between two directions [u₁ v₁ w₁] and [u₂ v₂ w₂] can be easily calculated from the expression

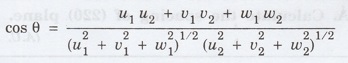
(ii) The normal to the plane with index number (h k l) is the direction [h k l].

(iii) The distance 'd' between adjacent planes of a set of parallel planes of the indices (h, k, l) is given by

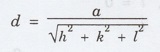
where 'a' is the edge (lattice constant) of the cube