Density of Energy States

DENSITY OF ENERGY STATES

The ability of a metal to conduct electricity depends on the number of quantum states and also the energy levels which are available for the electrons.

Hence, it is essential to find the energy states which are available for the occupation of the electrons (charge carriers).

Definition

It is defined as the number of available energy states per unit volume in an energy interval E and E +  dE.

It is denoted by Z (E). It is given by

Derivation

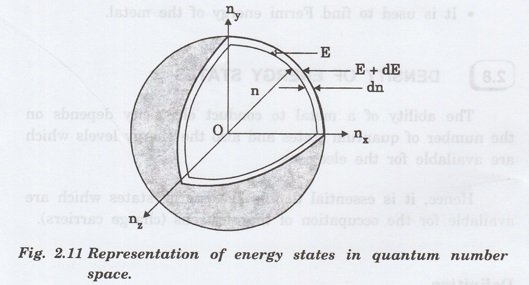
Let us consider a cubical metal of side 'a'. In order to find the number of energy states available in the metal in between the energy E and E + dE, a sphere is considered with three quantum numbers n_x, n_y, n_z as coordinate axes in three-dimensional space as shown in fig. 2.11.

A radius vector n is drawn from origin 'O' to a point with co-ordinates n_x, n_y, n_z in this space. All the points on the surface of the sphere have the same energy E.

Thus, n such that 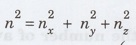 denotes the radius of the sphere corresponding to energy E .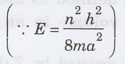

This sphere is further divided into many shells. Each shell represents a particular combination of quantum numbers (n_x, n_y, and n_z).

Therefore, a shell denotes a particular energy value E corresponding to a particular radius n. In this space, unit volume represents one energy state. (Fig. 2.12).

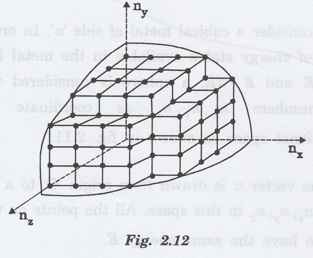
Thus, the volume of the sphere of radius n is equal to the number of energy states upto E.

Therefore, the number of energy states within a sphere of radius 'n'

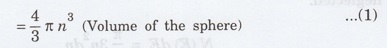
Since the quantum numbers n_x, n_y, n_z can have only positive integer values, only one octant of the sphere, i.e., (1/8)th of the spherical volume has to be considered.

Only one octant of the sphere has all the quantum numbers n_x, n_y and n_z as positive.

Therefore, the number of available energy states within one octant of the sphere of radius 'n' corresponding to energy E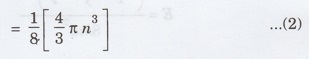 

Similarly, the number of available energy states within one octant of the sphere of radius 'n + dn' corresponding to energy E + dE

The number of available energy states between the shells of radii n and n + dn ie., between the energy values E and E + dE is determined by subtracting equation (2) from equation (3). Thus, we have

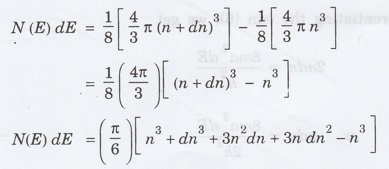
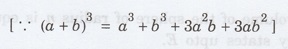
Since dn is very small, the higher powers dn² and dn³ are neglected.

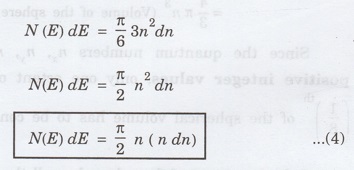
We know that the energy of an electron in a cubical metal piece of sides 'a' is given by (particle in a three dimensional box problem).

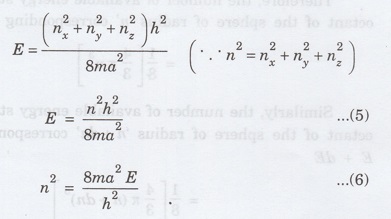
Taking square root of the eqn (6), we have

Differentiating the eqn (6), we get

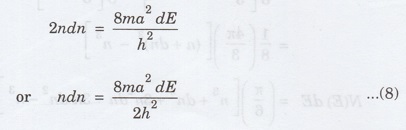
Substituting eqns (7) and (8) in eqn (4), we have

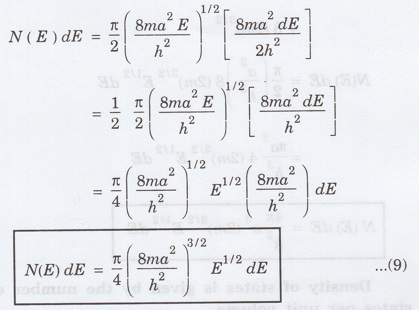
Pauli's exclusion principle states that two electrons of opposite spins can occupy each state. Hence, the number of energy states available for electron occupancy is given by

Density of states is given by the number of energy states per unit volume.

on substituting for N(E) dE and V, we have

Density of states

This is the expression for the density of states in energy between E and E + dE.

i. It is used to calculate carrier concentration in metals and semiconductors.

Carrier Concentration in Metals

Carrier concentration, i.e., the number of electrons per unit volume in a given energy interval is calculated by summing up the product of the density of states Z (E) and probability occupancy F (E).

Substituting for Z(E) and F(E), we have

For a metal at absolute zero temperature, the upper most occupied level is E_F, and all the levels are completely filled below E_F

F(E) =1 for the energy levels E = 0 to E = E_F at T = 0 K

Now, the equation (14) reduces to

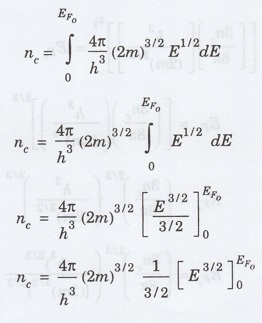
The equation (15) is used to calculate carrier concentration in metals and semiconductors in terms of Fermi energy.

Expression for Fermi energy

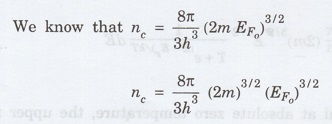
on rearranging, we have

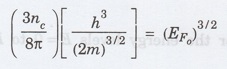
on raising to the power of 2/3 on both sides, we have

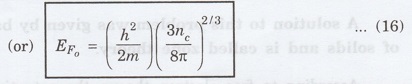
The equation (16) is the expression for Fermi energy of electrons in solids at absolute zero temperature.

i. It is noted that Fermi energy of a metal depends only on the density of electrons of metal.

Expression for Fermi Energy at T > 0 K

Fermi energy E_F at any temperature T in terms of Fermi energy at 0 K is given by the relation

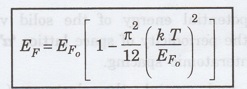
The second term within the bracket is very small compared to 1 (but has significant value at very high temperature). Hence, on neglecting that term, we get

E_F = E_Fo

Hence, the value of E_F can be taken equal to E_Fo itself.