Physics for Electronics Engineering: Unit II: Electrical and Magnetic Properties of Materials
Anna University Solved Problems in Electrical Properties of Materials
Anna university important solved problems in Electrical Properties of Materials
ANNA UNIVERSITY SOLVED PROBLEMS
Problem 2.4
Calculate
electrical conductivity in copper if the mean free path of electrons is 4 × 10-8
m, electron density is 8.4 × 1028 m-3 and average thermal
velocity of electron is 1.6 x 106 ms-1. (A.U Dec 2012)
Given data
Mean
free path of electron λ = 4 × 10-8 m
Electron density n = 8.4 × 1028 m-3
Average
thermal velocity of the electrons v = 1.6 x 106 ms-1
Charge
of an electron e = 1.6 × 10-19 coulomb
Mass
of an electron m = 9.11 x 10-31 kg
Solution

Problem 2.5
Calculate
electrical and thermal conductivities for a metal with a relaxation time 10-14
second at 300 K. Also, calculate Lorentz number using the above result (density
of electrons = 6 × 1028 m-3). (A.U. June 2013)
Given data
Relaxation
time t = 10-14 s
Temperature
T= 300 K
Electron
concentration n = 6 x 1028 m-3
Mass
of an electron m = 9.1 x 10-31 kg
Charge of an electron e = 1.6 x 10-19 C
Boltzmann’s
constant k = 1.38 × 10-23
JK-1
Solution
We
know that σ = n e2 τ / m
Substituting
the given values, we have
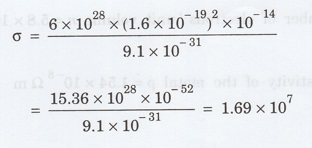
Electrical
conductivity σ = 1.69 × 107 Ω-1 m-1
Thermal
conductivity 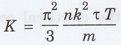
(By
quantum free electron theory)
Substituting
the given values, we have
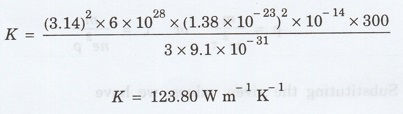
Lorentz
number L = K / σ T
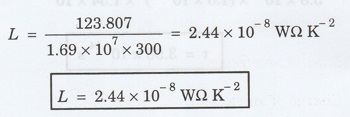
Problem 2.6
Find
the relaxation time of conduction electrons in a metal of resistivity 1.54 × 10-8
ohm-m if the metal has 5.8 × 1028 conduction electrons / m3.
(A.U. May 2008)
Given data
Number
of electrons / unit volume n = 5.8 × 1028 m-3
Resistivity
of the metal p = 1.54 × 10-8
Ω m
Solution
We
know that the electrical conductivity of a metal
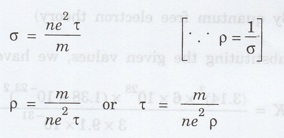
Substituting
the given values, we have

Problem 2.7
A
uniform silver wire has a resistivity of 1.34 × 10-8 Ω m at room
temperature for an electric field of 1 volt/cm. Calculate (i) the drift
velocity (ii) the mobility and (iii) the relaxation time of electrons assuming
that there are 5.8 × 1028 conduction electrons m-3 of the
material. (A.U. May 2009)
Given data
Resistivity
of the wire p = 1.34 × 10-8 Ω m
Electrical
field E = 1 V/cm = 1 V/ 10-2 m = 1 × 102 Vm-1
Number
of electron per unit volume n = 5.8 × 1028 m-3
Solution
Electrical
conductivity 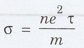
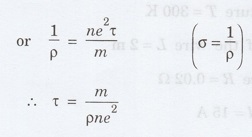
Substituting
the given values, we have
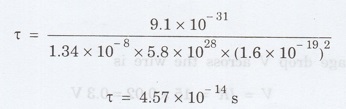
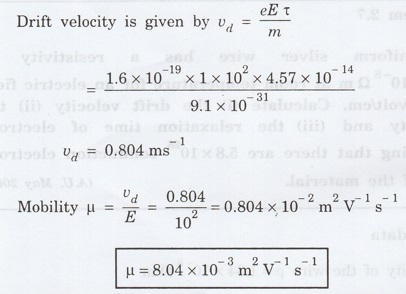
Problem 2.8
Calculate
the drift velocity and thermal velocity of conduction electrons in copper at a
temperature of 300 K. When a copper wire of length of 2 m and resistance 0.02 Ω
carries a current of 15 A.
Given
mobility μ= 4.3 × 10-3 m2 V-1s-1
(A.U. Jan 2014)
Given data
Temperature
T = 300 K
Length
of the wire L = 2 m
Resistance
R = 0.02 Ω
Current
I= 15 A
Mobility
μ= 4.3 × 10-3 m2 V-1s-1
Solution
Voltage
drop V across the wire is
V = I R = 15 × 0.02 = 0.3 V
Electric
field E across the wire is given by
E
= V/L = 0.3/2 = 0.15 Vm-1
Drift
velocity
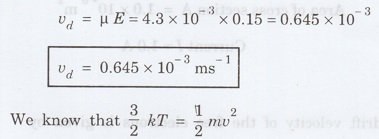
where
v is thermal velocity
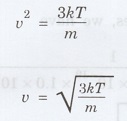
Substituting
the given values, we have
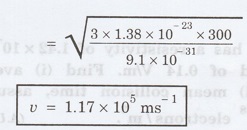
Problem 2.9
Find the drift velocity of the free electrons in a copper wire whose cross sectional area is 1.0 mm2 when the wire carries a current of 1A. Assume that each copper atom contributes one electron to the electron gas. Given n = 8.5 × 1028 m-3 (A.U. May 2016)
Given Data
Conduction
electron / m3, n = 8.5 × 1028 m-3
Charge
of electron e = 1.6 × 10-19 C
Area
of cross section A = 1.0 × 10-6 m2
Current
I = 1.0 A
Solution
The
drift velocity of the free electrons is given by
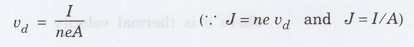
Substituting
the given values, we have

Problem 2.10
A
metallic wire has a resistivity of 1.42 × 10-8 Ω m. For an electric
field of 0.14 V/m. Find (i) average drift velocity and (ii) mean collision
time, assuming that there are 6 × 1028 electrons /m3.
(A.U.
April 2015)
Given data
Electric
field E = 0.14 Vm-1
Resistivity
p = 1.42 × 10-8 ΩΜ
Number of electrons per unit volume n = 6 × 1028 m-3
Charge
of the electron e = 1.6 × 10-19 C
Mass
of an electron m = 9.1 × 10-31 kg
Solution:
The
resistivity of a metal is given by,

Substituting
the given values, we have
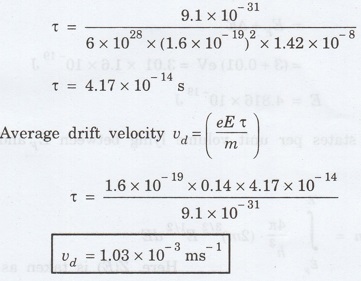
Density of energy states
Problem 2.11
Calculate the number of states lying in an energy interval of 0.01 eV above the Fermi level for a crystal of unit volume with Fermi energy EF = 3 eV (A.U. June 2010)
Given data
Mass
of electron m = 9.1 × 10-31 kg
Energy
interval ∆E = 0.01 eV
Planck’s
constant h = 6.63 × 10-34 Js
Fermi
energy EF = 3 eV [‘.’ 1 eV = 1.6 × 10-19 J]
EF
= 3 × 1.6 × 10-19 J
EF
= 4.8 × 10-19 J
Solution
We
know that ∆E = E - EF = EF + ∆E = (3 + 0.01) eV = 3.01 ×
1.6 × 10-19 J
E
= 4.816 × 10-19
Number
of states per unit volume lying between EF and E is given by
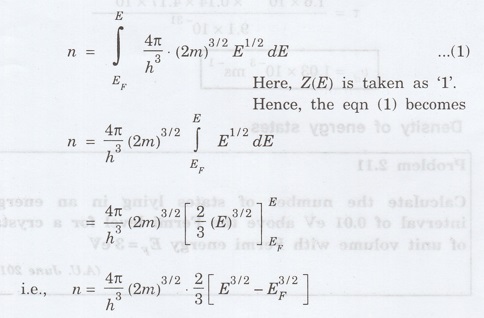
Substituting
the given values, we have
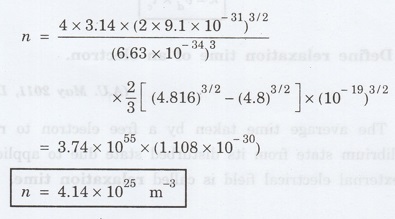
Physics for Electronics Engineering: Unit II: Electrical and Magnetic Properties of Materials : Tag: : - Anna University Solved Problems in Electrical Properties of Materials
Related Topics
Related Subjects
Physics for Electronics Engineering
PH3254 - Physics II - 2nd Semester - ECE Department - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
