Accounting for Finite Permeability and Core Loss

ACCOUNTING FOR FINITE PERMEABILITY AND CORE LOSS

We will consider two cases:

(i) when a transformer is on no load,

(ii) when it is loaded.

Transformer on No-Load

In above discussion, we assumed an ideal transformer (i.e.,) one in which there were no core losses and copper losses. When an actual transformer is put on load, there is iron loss in the core and copper loss in the windings (both primary and secondary) and these losses are not entirely negligible.

When the transformer is on no load, the primary input current is not wholly reactive. The primary input current under no-load condition has to supply:

i. iron losses in the core (i.e.,) hysteresis loss and eddy current loss.

ii. A very small amount of copper loss in primary (there being no cu loss in secondary as it is open). Hence, the no-load primary input current I₀ is not at 90° behind V₁ but logs it by an angle φ₀ angle 90°. No load input power

W₀ = V₁ I₀ cos φ₀

cos φ₀ - Primary power factor under no load condition. Its vector diagram is shown in Figure 1.12.

Primary currents I₀ has two components:

i. I_ω is in phase with V₁. This is known as active or working (or) iron loss component I_ω because it mainly supplies the iron loss plus small quantity of primary Cu loss.

I_ω = I₀ cos φ₀

ii. The other component is in quadrature with V₁ and is known as magnetizing component I_µ because its function is to sustain the alternating flux in the core. It is wattless.

I_µ = I₀ sin φ₀

I₀ is the vector sum of I_ω and I_µ

I₀ = (I_µ² + I_ω²)

Some of Points to be Noted:

1. The no load primary current I₀ is very small as compared to the full load primary current. It is about 1 per cent of the full load current.

2. Owing to the fact that the permeability of the core varies with the instantaneous To som value of the exciting current, the wave of the exciting or magnetizing current is the wave not truly sinusoidal. It should not be represented by a vector because only sinusoidally varying quantities are represented by rotating vectors. But in practice, it makes no appreciable difference.

3. As I₀ is very small, the no load primary cu loss is negligibly small which means that no load primary input is practically equal to the iron loss in the transformer.

4. The core-loss which is responsible for shift in the current vector, angle φ₀ is known as hysteresis angle of advance.

Example 1.7:

(a) A 2,200/200 V transformer draws a no-load primary current of 0.6 A and absorbs 400 Watts. Find the magnetizing and iron loss current.

(b) A 2,200/250 V transformer takes 0.5 A at a p.f of 0.3 on open circuit. Find magnetizing and working components of no load primary current.

Solution:

Example 1.8:

A single phase transformer has 500 turns on the primary and 40 turns on the secondary winding. The mean length of the magnetic path in the iron core is 150 cm and the joints are equivalent to an air gap of 0.1 mm. When a potential difference of 3000 V is applied to the primary. Maximum flux density is 1.2 Wb/m₂. Calculate (a) the cross sectional area of the core, (b) no load secondary voltage, (c) the no load current drawn the primary, (d) power factor on no load. Given that AT/cm for a flux density of 1.2 Wb/m₂ in iron to be 5, the corresponding loss to be 2 watt/kg at 50 Hz and the density of iron as 7.8 gram/cm³.

Solution:

E₁ = 4.44 f B_m A

3000 = 4.44 × 50 × 1.2 × A

A = 3000/4.44 × 50 × 1.2 = 0.0225 m²

A = 225 cm².

This is the net cross-sectional area. However, the gross area would be about 10% more to allow for the insulation between laminations.

(b) k = N₂ / N₁ = 40/500 = 4/50

No load secondary voltage = KE₁ = (4/50) × 3000 = 240V.

(c) AT per cm = 5: AT for iron core = 150 × 5 =750

AT for air gap = Hl = (B/ µ₀) × l = (1.2/4п ×10^-7) ×0.0001 = 95.5

Total AT B_max­ = 750 + 95.5 = 845.5.

Maximum value of magnetizing current drawn by primary = 845.5/500 = 1.691 A

Assuming this current to be sinusoidal, its rms value is I_µ = 1.691/√2 = 1.196 A

Volume of iron = length × Area = 150 × 225 = 33,750 cm³

Density = 7.8 gram/cm³

Mass of iron = 33,750 × 7.8/1000 = 263.25 kg

Total iron loss = 263.25 × 2 = 526.5 W.

Iron loss component of no load primary current I₀ is:

Transformer on Load

When the secondary winding is connected to a load, then transformer is said to be on load as shown in Figure 1.13. I₂ current will flow through the load, when the transformer is connected to load. The magnitude and phase of I₂ with respect to V₂ is determined by the characteristics of the load.

Current I₂ is in phase with V₂ if load is resistive. If it is inductive load, I₂ lags V₂. If I₂ leads V₂ then it is the response of capacitive load. At no load condition No load current I₀ will flow through primary winding of transformer which is shown in figure and I₀ setup the flux φ.

Under loaded condition, secondary current I₂ produces the φ₂ which is in opposition to the main primary flux φ which is produced due to I₀. The secondary ampere turns are called as demagnetizing ampere-turns. The opposing flux φ₂ weakness the primary flux φ momentarily, so that back emf E₁ is reduced. For a moment V₁ gains the upper hand over E₁ and hence causes more current (I₂) to flow in primary. It is called as load components of primary current. It is opposition with I₂. Hence φ₂' and φ₂ cancels each other shown in Figure 1.13 and 1.14.

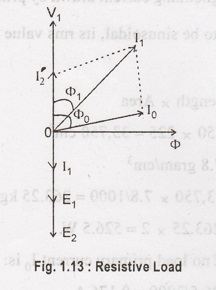
Hence, whatever the load conditions, the net flux passing through the core is approximately the same as at no load. Due to constancy of core flux at all loads, the core loss is also practically the same under all load condition.

φ₂ = φ₂'

N₂ I₂ = N₁ I₂'

I₂' = (N₂/N₁) × I₂

I₂' = k I₂.

When the transformer is on load, the primary winding has two current in it. The total primary current is the vector sum of I₀ and I₂'

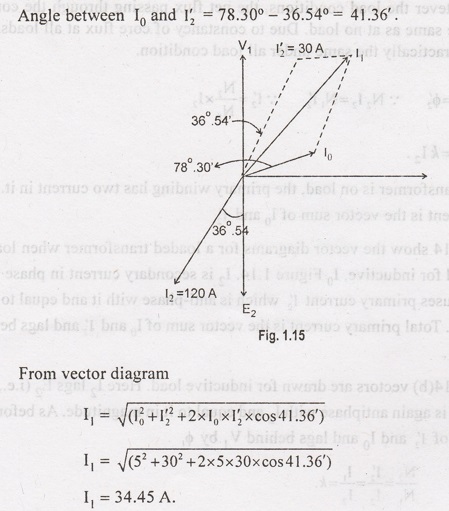
In Figure 1.14 show the vector diagrams for a loaded transformer when load is non-inductive and for inductive, I₀ Figure 1.14. I₂ is secondary current in phase with E₂ (i.e., V₂). It causes primary current I₂' which is anti-phase with it and equal to it in magnitude (k = 1). Total primary current is the vector sum of I₀ and I₂' and lags behind V₁ by an angle φ.

In Figure 1.14(b) vectors are drawn for inductive load. Here I₂ lags E­₂ (i.e., V₂) by φ₂. Current I₂' is again antiphase with I₂ and equal to it in magnitude. As before, I₁ is the vector sum of I₂' and I₀ and lags behind V_1­ by φ₁

N₂/N₁ = I₂'/I₂ = I₁/I₂ = k

Example 1.9:

A single phase transformer with a ratio of 440/110 V takes a no-load current of 5A and 0.2 power factor lagging. If the secondary supplies a current of 120 A at a p.f of 0.8 lagging. Estimate the current taken by the primary.

Solution:

Example 1.10:

A transformer has a primary winding of 800 turns and a secondary windings of 200 turns. When the load current on the secondary is 80 A at 0.8 power factor lagging. The primary current is 25 A at 0.707 power factor lagging. Determine the no load current of the transformer and its phase with respect to the voltage.

Solution:

Transformer Winding Resistance and Reactance

In practical transformer, the windings having some resistance. The primary winding has primary resistance. It is called as R₁, R₂ is the secondary resistance of secondary winding.

In practical transformer, all the flux generated by the primary does not link the secondary winding. Some flux passes through air instead of flowing through the core. This called primary leakage flux (φ_L1). It induce an emf L₁ in primary winding. φ_L1 is in phase with I₁. Similarly flux also setup in the secondary winding. This flux is called secondary leakage flux. (φ_L2). φ_L2 induces the emf eL₂ in secondary winding and doesnot links the primary winding. It is in phase with I₂.

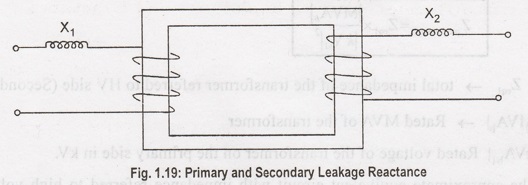
Primary and Secondary Fluxes are shown in Figure 1.18. At no load and light loads, the transformer carries only small current so leakage fluxes are negligible. Under heavy load conditions, the transformer primary and secondary windings carry large currents. Due to this, the leakage reactance X₁ and secondary leakage reactance X₂ are shown in Figure 1.19.

The practical transformer should have winding resistances and leakage reactance i.e., R₁, R₂, X₁ and X₂. It is shown in Figure 1.20