Simple Cubic (SC) Structure

STRUCTURE AND PACKING FRACTIONS OF CRYSTALS

It is noted that a large number of metallic crystal structures have hcp, fcc and bcc structures. Simple Cubic (SC) structure is very rare in metals.

The alkali metals Li, Na, K, etc., have bcc structures, some transition elements and rare earths have fcc structures, elements of second group have hcp structures.

SIMPLE CUBIC (SC) STRUCTURE

The simple cubic structure is the simplest and easiest crystal structure. In this structure, there is one atom at each of the '8' corners of unit cell. These atoms touch each other along cube edges. (fig 1.12).

1. Number of atoms per unit cell

The unit cell of a simple cubic structure is shown in fig 1.12. The representative arrangement is drawn in fig. 1.12 (a). The actual way of arrangement is shown in Fig. 1.12 (b).

There are 8 atoms, one atom at each corner of unit cell. Each corner atom is shared by 8 adjacent unit cells. (Fig. 1.13)

Share of each unit cell = (1/8) of corner atoms = (1/8) x 8 = 1

Total number of atoms in one unit cell = 1 atom

2. Coordination number

Simple cubic unit cell has 8 corner atoms. Let us consider one of the corner atoms (say X). It is shared by 8 adjacent unit cells as shown in fig 1.14.

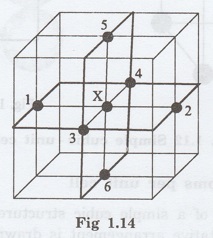
There are 4 nearest neighbouring atoms to this particular atom 'X' which are shown by 1, 2, 3, and 4 in a plane (horizontal plane). Further, there are 2 more nearest atoms, one directly above (atom 5) and the other one directly below (atom 6) the atom X.

Thus, there are only six (4+2) nearest neighbours for the atom X.

Hence, coordination number for simple cubic is 6.

Note: Similarly if we consider any corner atom, the total number of nearest neighbours i.e., the co-ordination number is the same.

3. Atomic radius

Consider a face of unit cell of a simple cubic structure (fig 1.15). The atoms touch each other along the edges of the cube.

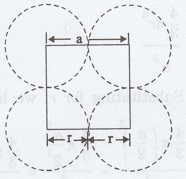
Fig 1.15 Face view of simple cubic - unit cell

It is clear that the distance between the centres of two nearest atoms is equal to the cube edge a.

If 'a' is the side of the unit cell and r its radius, then, from fig. 1.15,

2r = a

r = a/2

4. Packing factor

Number of atoms per unit cell = 1

Volume of the atoms in the unit cell, v = 1 x (4/3)πr³

Atomic radius r = a/2

Total volume of the unit cell, V = a³

We know that packing factor = v / V

Substituting for v and V, we have

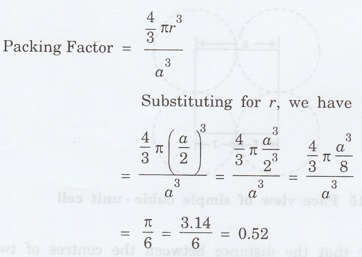
Packing factor = 0.52 x 100 %

PF = 52%

Thus, 52% of the volume of unit cell is occupied by the atoms and the remaining 48% volume is vacant.

Example: Only one element polonium (Po) at certain temperature range exhibits this crystal structure.