Planes in Crystals and Miller Indices

PLANES IN CRYSTALS

A crystal lattice is considered as a collection of a set of parallel equidistant planes passing through lattice points. These planes are known as lattice planes.

These sets of planes may be chosen in many different ways in the given lattice, for example (a), (b), (c), (d), etc. as in fig. 1.32. Now, the problem that may arise is how to designate (identify) a plane in a crystal.

MILLER INDICES

Miller introduced a set of three numbers to designate the orientation of a plane in a crystal. This set of three numbers is called Miller indices of the concerned plane.

Explanation

The orientation of a plane in a crystal is usually described in terms of their intercepts on the three axes.

For example, a plane ABC in fig. 1.33 has intercepts of 2 axial units on X-axis, 2 axial units on Y-axis and 1 axial unit on Z-axis. In other words, the numerical parameters of this plane are 2, 2 and 1. Hence, its orientation is (2, 2, 1).

Miller suggested that it is better to describe the orientation of a plane by the reciprocal of coefficient of intercepts (numerical paraments)

These reciprocals are converted into whole numbers and they are known as Miller indices of the concerned plane.

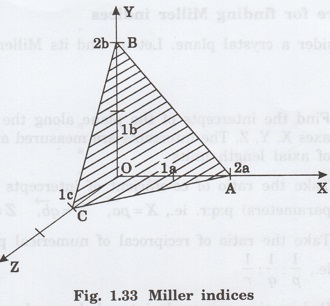
Hence, Miller indices of a plane ABC (fig. 1.31) are (1/2 : 1/2 : 1) or simply (112).

We understand that for getting the whole numbers, all three reciprocals of the co-efficients of intercepts are multiplied by 2 (LCM). It is noted that multiplying all numerical parameters by the same number does not change the orientation of a plane.

The numbers for these planes a written within parentheses and not in brackets.

The general expression for Miller indices of a plane is (h k l). The symbol for a family of parallel planes is < h k l >.

Definition

Miller indices are the smallest possible three integers that have the same ratios as the reciprocals of the numerical parameters of the plane concerned on the three axes.

Procedure for finding Miller indices

Consider a crystal plane. Let us find its Miller indices as follows.

Step 1 Find the intercepts of the plane along the coordinate axes X, Y, Z. The intercepts are measured as multiples of axial length units

Step 2 Take the ratio of co-efficient of intercepts (numerical parameters) p:q:r. ie.,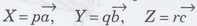 

Step 3 Take the ratio of reciprocal of numerical parameters ie., 1/p : 1/q : 1/r

Step 4 Reduce the reciprocals into whole numbers. This can be done by multiplying each reciprocal by a number obtained after taking LCM (Least Common Multiple) of the denominators.

Step 5 Write these integers within parantheses without commas to get Miller indices.

ANNA UNIVERSITY SOLVED PROBLEM

Problem 1.4

Obtain Miller indices of a plane whose intercepts are 4, 4 and 2 units along the three axes. (A.U. Jan 2010)

Solution

Numerical parameters are 4, 4, 2.

Reciprocal of these are 1/4, 1/4, 1/2.

LCM of denominators 4, 4 and 2 is 4. Hence, multiplying by 4, we have 1, 1, 2. Thus, the Miller indices of this plane is (1 1 2).

Miller indices of cubic crystal planes

While finding Miller indices of a cubic crystal plane, the following points should be kept in mind.

(i) When a plane is parallel to one of the coordinate axes, it is said to meet that axis at infinity. Since 1/∞ = 0.  Miller index for that axis is zero.

(ii) When the intercept of a plane is on the negative part of any axis, Miller index is distinguished by a bar put directly over it.

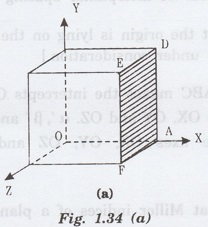
Consider a shaded plane in fig. 1.34 (a). This plane ADEF cuts X-axis at the point A and it is parallel to Y and Z axes. If the side of the cube is taken as one unit in length, then intercepts made by this plane on three axes are

1: ∞: ∞

The reciprocals of the intercepts are

1/1: 1/∞: 1/∞

ie., 1 : 0 : 0

Hence, Miller indices of this plane are (100).

The plane ABC in fig. 1.34 (b) has equal intercepts on the three axes and hence its Miller indices are (111). Miller indices of the plane GBAF are (110) as shown in fig. 1.34 (c).