Optical Processes in Quantum Wells

OPTICAL PROCESSES IN QUANTUM WELLS

The term "Well" refers to a semiconductor region that is grown to possess a lower energy, so that it acts as a trap for electrons and holes. These are called quantum wells because these semiconductor regions are only a few atomic layers thick. Quantum wells are real-world implementation of the "particle in one-dimensional box" problem.

The basic properties of a quantum well is understood from the simple 'particle in a box' model. In quantum well an isolated thin semiconductor sheet of thickness L is considered as length of the box.

Solving the Schroedinger equation and applying boundary conditions result in the following quantized energies for charge carrier.

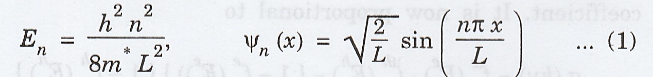
n = 1, 2, …….. ∞

h - Planck's constant

m - mass of charge carrier (electron or hole)

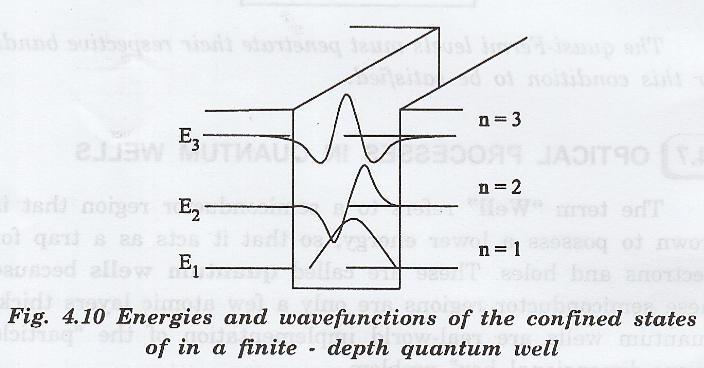
Finite quantum wells are formed by sandwiching a thin layer (<50 nm) of one semiconductor (GaAs) between two layers of another larger band gap semiconductor (AlGaAs) barriers. This finite depth potential well is shown in fig. 4.10.

The fig. 4.10 shows energies and wave functions for a finite depth well. The energy of the first allowed electron energy level in a typical 100 Å GaAs quantum well is about 40 meV calculated using eqn (1).

The optical transition is proportional to the density of states at the initial point in the valence band and the final point in the conduction band.

The energy absorption spectrum therefore exhibits a very different form for nanostructures of different dimensionality.

 In quantum wells for confined the direction instead of momentum conservation a selection rule applied. This rule states that only transition between states of the same quantum number in the VB and CBs are allowed.

This rule follows from the fact that the optical absorption strength is proportional to the overlap integral of the conduction and valence wavefunctions. (Fig. 4.11)

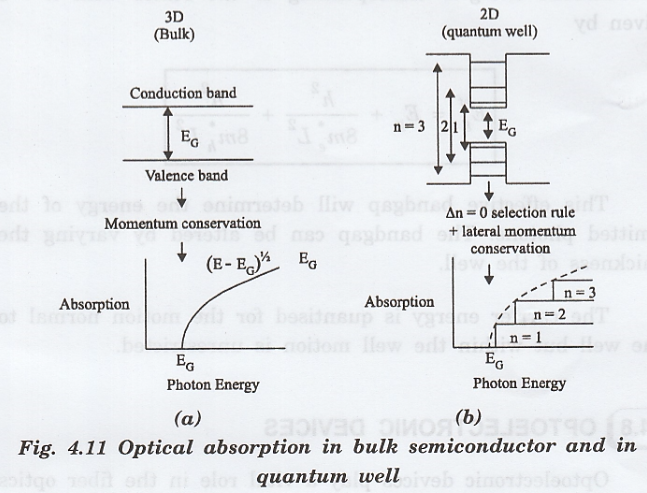
In quantum well the electrons and holes are still free to move in the directions parallel to the layers. Therefore, there is deviation in discrete energy states for electrons and holes.

There are 'subbands' that start at corresponding to each of the energies calculated for the confined states.

The density of state turns out to be a 'step' that starts at the appropriate confinement energy.

Optical transitions must still conserve momentum in this direction and just as for bulk semiconductors. The optical absorptions must still therefore follow the density of states. Hence in this simple model, the optical absorption in a quantum well is a series of steps with one step for each quantum number 'n', as shown in fig. 4.11 (b).

consequence of quantum confinement in quantum well, the effective band gap of a semiconductor E increases from its bulk value by the addition of the electron and hole confinement energies corresponding to the states with n = 1 given by

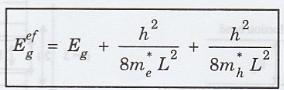
This effective bandgap will determine the energy of the emitted photons. The bandgap can be altered by varying the thickness of the well.