Important Two Marks & 16 Marks Question and Answers

ANNA UNIVERSITY PART - A '2' Marks Q&A

1. What is a space lattice? (A.U. May 2008, Dec 2009)

It is an array of points in three dimensions in which every point has an identical surrounding.

 

2. What is a unit cell? (A.U. May 2011, Jan 2009)

It is the smallest volume of a solid from which the entire crystal structure can be constructed by repetition in three-dimension.

 

3. Name the seven crystal systems. (A.U. Jan 2010)

(i) Cubic (ii) Tetragonal (iii) Orthorhombic (iv) Monoclinic (v) Triclinic (vi) Rhombohedral

(vii) Hexagonal

 

4. What is a primitive cell? (A.U. May 2011)

A primitive cell is the simplest type of unit cell which contains only one lattice point per unit cell.

 

5. Name the crystal structure of the following: (a) Gold (b) Germanium (c) Barium (d) Zinc

(A.U. Dec 2008)

(a) Gold - FCC (b) Germanium - Diamond cubic (c) Barium - BCC (d) Zinc – HCP

 

6. Bismuth has a = b = c = 4.74 Å and angles α = β = γ = 60°. What is its crystal structure?

(A.U. Nov 2008)

Given a = b = c = 4.74 Å, α = β = γ = 60°

Since a = b = c and α = β = γ ≠ 90°

The crystal structure of Bismuth is trigonal (Rhombohcdral)

 

7. What are Bravais lattices? od (A.U. May 2010, Jan 2012)

There are only 14 ways of arranging points in 3 - dimensional space such that the environment looks same from (010 D each point. ie., there are 14 possible types of space lattices out dub of the seven crystal systems. These 14 space lattices are called Bravais lattices.

 

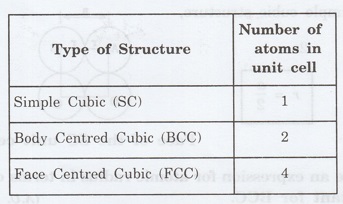
8. Give the values of number of atoms in unit cell for SC, BCC, FCC. (A.U. Jan 2008, 2009)

 

9. Define coordination number. (A.U. Dec 2010)

It is the number of nearest neighbouring atoms that any atom has in the given crystal structure.

 

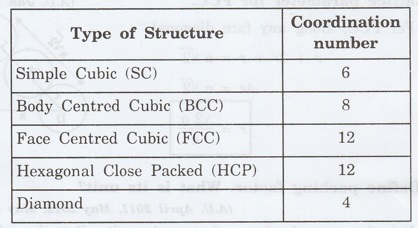
10. Give the coordination numbers for SC, BCC, FCC, HCP and Diamond (A.U. May 2009)

 

11. Define atomic radius. (A.U. Jan 2011)

The half of the distance between nearest neighbouring atoms in a crystal is known as atomic radius. The atomic radius is denoted by 'r' and it is usually expressed in terms of the cube edge 'a' (lattice parameter).

 

12. Obtain the formula for atomic radius 'r' in terms of (e lattice constant 'a' for simple cubic.

(A.U. Dec 2009)

In simple cubic structure,

2r = a

r = a/2

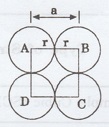
Face of the SC unit cell

 

13. Arrive an expression for atomic radius in terms of lattice constant for BCC. (A.U. May 2012)

In BCC, along the body diagonal AG,

r + 2r + r = a√3

4r = a √3

r = √3 a / 4

 

14. Derive an expression for atomic radius in terms of lattice parameter for FCC. (A.U. Jan 2011)

For FCC, along any face diagonal,

r + 2r + r = a √2

4r = a √2

r = a√2 / 4

 

15. Define packing factor. What is its unit? (A.U. April 2011, May 2012, May 2013)

It is the ratio of volume of atoms in unit cell to the volume of the unit cell. It has no unit, since it is a ratio of same physical quantity.

 

16. Calculate packing factor in the case of simple cubic structure. (A.U. Dec 2012)

Packing factor = Volume occupied by the atoms in a unit cell (v) / Volume of unit cell (V)

 

17. Calculate packing factor of body centred cubic crystal. (A.U. May 2013)

Packing factor = Volume occupied by the atoms in a unit cell / Volume of the unit cell

Number of atoms per unit cell = 2

For BCC, Atomic radius r = √3 a / 4

 

18. Calculate the packing factor of face centred cubic crystal. (A.U. May 2012)

Packing factor = Volume occupied by the atoms in a unit cell / Volume of unit cell

Number of atoms per unit cell = 4

 

19. What are Miller indice? (A.U. May 2010, Jan 2011)

A set of three numbers to designate a plane in a crystal is known as Miller indice of the concerned plane, symbolised by (h k l)

The reciprocal of the intercepts made by the plane on the cryptallographic axes which are reduced to smallest integers.

 

20. Give the expression for interplanar spacing for a cubic system interms of lattice constant and Miller indices. (A.U. Jan 2012)

Interplanar spacing d =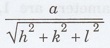 

a - lattice constant

h, k, l Miller indice

 

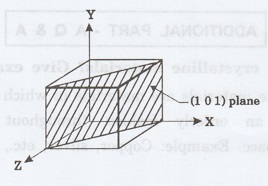
21. Sketch the (101) plane in a cubic system. (A.U. May 2008, Jan 2009)

 

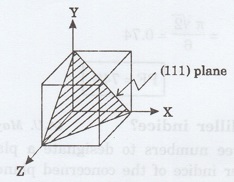
22. Sketch (111) plane for a cubic crystal. (A.U. May 2010, Jan 2011)

 

23. Obtain Miller indices of a plane whose intercepts are a, b/2, 3c in a simple cubic unit cell.

(A.U. Jan 2010)

Actual intercepts are a, b/2, 3c

Numerical parameters are 1, 1/2, 3

Reciprocals of the above 1, 2, 1/3

Miller indices of the plane is (3 6 1)

 

ADDITIONAL PART A Q & A

1. What are crystalline materials? Give example.

Crystalline materials are materials in which the atoms are arranged in an orderly fashion throughout in a three dimensional space. Example: Copper, silver, etc.,

 

2. What is an amorphous solid? Give example.

It is a type of solid in which the atoms are not arranged in an orderly fashion. (randomly).

 

3. What is a crystal?

A crystal is a three dimensional solid composed of a periodic and regular arrangement of atoms.

 

4. What are lattice points?

The points in the space to represent position of atom or group of atoms of the crystal are called lattice points.

 

5. What is basis?

The crystal structure is formed by associating with every lattice point a unit assembly of atoms or molecules (ie, one or more atoms or molecules). This unit assembly is called the basis or pattern.

 

6. What are the differences between crystalline and old non-crystalline material.

 

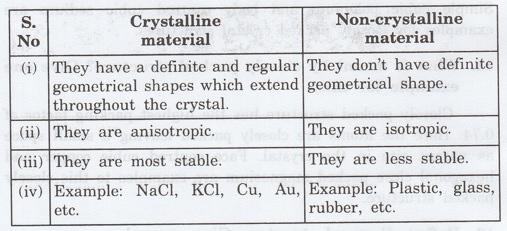
7. What are the lattice parameters of an unit cell?

The intercepts on the axes a, b and c and interfacial angles α, β and γ are called lattice parameters of an unit cell.

 

8. Define inter-atomic distance and interplanar distance.

Interatomic distance: It is the distance between the centres of any two nearest atoms.

Inter-planer distance: It is the perpendicular distance between any two parallel planes.

 

9. What is the relation between lattice constant 'a' and density 'p' of the crystal?

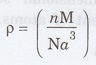
where,

n - Number of atoms in unit cell

M - atomic weight

N - Avagadro's number = 6.023 x 10²⁶ mol^-1

 

10. What is meant by loosely packed crystal structure? Give an example of this type of material.

The loosely packed crystal structure has the packing factor less than 0.74. That is, in which more vacant site is available. Simple cubic polonium and body centred cubic sodium are examples for loosely packed crystal structures.

 

11. What is meant by closely packed structure? Give one example for this.

Closely packed structure has the highest packing factor of 0.74. Here the atoms are closely packed leaving a small space as vacant site in the crystal. Face centred cubic copper and hexagonal close packed magnesium are examples to this closely packed structure.

 

12. Define diamond structure Give example.

Germanium, silicon and diamond possess a structure which is a combination of two interpenetrating FCC sub-lattices shifted along the body diagonal by 1/4 th of cube edge.

 

13. What is crystal defect?

The deviation from the regularity of arrangement of atoms is called crystal imperfection or crystal defect.

 

14. What are the various types of defects?

I. Point defects (zero dimensional)

(a) Impurity defect

(i) Substitutional impurity defect

(ii) Interstitial impurity defect

(b) Vacancies

(i) Frenkel defect

(ii) Schottky defect

II. Line defects (one dimensional)

(a) Edge dislocation

(b) Screw dislocation

III. Surface defects (two dimensional)

(a) Grain boundaries

(b) Twin boundaries olla

(c) Tilt boundaries

(d) Stacking faults

(e) Ferromagnetic domain walls

IV. Volume defects (three dimensional)

(a) Cavities or voids

(b) Cracks and holes

 

15. What is impurity defect? What are the types of impurity defects?

A foreign substance added to a crystal is called impurity. The impurity atom may fit in the structure in two ways giving rise to two kinds of impurity defects.

(i) Substitution impurity defect

(ii) Interstitial impurity defect

 

16. What are vacancies?

Vacancies are empty atomic sites. Vacancies may occur as a result of imperfect packing during the original crystallization or they may arise from the thermal vibrations of atoms at higher temperatures.

There are different kinds of vacancies like Frenkel defect, Schottky defect, Colour centers etc.

 

17. What is Frenkel defect?

A vacancy associated with interstitial impurity is called Frenkel defect.

 

18. What is Schottky defect?

If an atom is missing from its lattice site, the vacancy is called Schottky defect.

 

19. What is line defect? What are its type?

The defect along a line is called line defect. There are two types of line defects

(i) Edge dislocation and

(ii) Screw dislocation.

 

20. What are twin boundaries?

If the atomic arrangement on one side of the boundary is the mirror image of the arrangement on the other side the defect is called twin boundaries.

 

21. What is stacking fault?

This defect arises due to defect in the stacking of atomic planes. In some cases a part of certain atomic plane will be missing where as in some other cases a portion of extra atomic plane is present, changing the sequence of arrangement of atoms.

 

ANNA UNIVERSITY PART B (16 Marks) Questions

1. Define the terms atomic radius and packing factor. Calculate the above for SC, BCC and FCC structures. (A.U. Dec 2012)

2. Calculate the number of atoms per unit cell, coordination number and packing factor for FCC and BCC structures. (A.U. Dec 2013)

3. What is packing factor? Prove that the packing factor of HCP is 0.74. (A.U. May 2012)

4. What are Miller indices? Sketch two successive (110) planes. Show that for a cubic lattice the distance between two successive plane (h k l) is given by  (A.U. May 2012)

5. (i) What are Bravais lattices?

(ii) Derive an expression for the interplanar spacing in a cubic structure. (A.U. Jan 2009)

6. (i) What are Miller indices?

(ii) Derive an expression for the interplanar spacing of (h k l) planes of a cubic structure.

(A.U. Jan. 2009, Jan 2010, Jan 2013)

7. (i) What are Bravais lattices? Describe using diagrams of unit cell the different Bravais lattices and their grouping into the seven crystal systems.

(ii) Describe the arrangement of atoms in FCC and HCP structures and show that both these structures have the same atomic packing factor. (A.U. Jan 2010, 2011)

8. Explain diamond cubic structure and obtain its atomic dis packing factor. (A.U. Jan 2010)

9. Give the procedure for finding Miller indices of crystal A e planes. (A.U. Jan 2010)

10. (i) Draw the standard crystal systems with their lattice parameters. What are Bravias lattices?

(ii) Explain the procedure to obtain the Miller indices of crystal planes. Also deduce a relation between Miler indices and the inter-planar distance. (A.U. Jan 2011)

11. (i) What is packing factor? Obtain packing factors for SC, BCC and FCC lattices.

(ii) Describe the crystal structure of diamond. (A.U. Jan 2011)

12. Describe the diamond structure. What type of bond is present in diamond? (A.U. Jan 2012)

 

ADDITIONAL PART B (16 Marks) Questions

1. (a) Explain (i) space lattice (ii) Basis (iii) unit cell

(b) Explain the various types of crystal systems with an example for each.

2. What are the lattice parameters of a unit cell? Describe Bravais lattices.

3. Explain crystal defects in a detailed manner.

 

ASSIGNMENT PROBLEMS

1. In a SC crystal system, the closest distance between its neighbouring atoms is 2.62 Å. Calculate the spacing between (100), (110) and (111) planes. (Ans. 2.62Å, 2.62Å/√2, 2.62 Å/√3)

2. Calculate the lattice constant of Molybdenum with BCC structure and density of 10.2 x 10³ kg/m³. The atomic weight of Molybdenum is 95.94. (Given Avagadro number is 6.02 × 10²⁶)

(Ans: 3.149 Å)

3. The lattice constant of a metal with cubic lattice is equal to 2.88 Å. The density of the metal is 7.20 gm/cm³. Calculate the number of unit cell present in 1 kg of metal. (Ans: 5.8 x 10²⁴)

4. Copper crystallises in the FCC structure. The density and atomic weight of copper are 8960 kg/m³ and 63.54 respectively. Calculate its lattice constant. (Ans: 3.6 Å)

5. The atomic packing efficiency of a crystal is 68% and the closest distance of approach between its neighbouring atom is 2.62 Å. Calculate density of the crystal if the mass of its one atom is 50.04 amu. (Ans. 6000 kg/m²)

6. Ni has FCC structure with lattice constant 3.52 Å. Calculate the interplanar spacings for (a) (101) plane (b) (123) plane (c) (320) plane. (Ans. 2.49 x 10^-10 m, 9.41 x 10^-11 m and 9.76 x 10^-11m)

7. Diamond crystallizes in ZnS structure. Calculate its density, given that the cube edge for diamond is 3.57 Å and the atomic weight of carbon is 12.01. (Ans. p = 3508 kg/m³ Take n = 8 since, ZnS structure consists of two inter penetrating FCC structure)

8. The interplanar spacing of (110) plane is 2 Å for a cubic crystal. Find out the atomic radius.

(Ans. a=2√2 Å, Assuming FCC structure r = 10^-10 m)

9. Determine the Miller indices of a plane that makes intercepts 2 Å, 3 Å and 4 Å on the co-ordinate axes of an orthorhomibic cyrstal with a:b:c = 4:3:2. (Ans. (421))

10. Calculate the interplanar spacing for (321) plane in simple cubit crystal lattice with interatomic spacing a = 4.12 (Ans. d = 1.01 Å)