Bravais Lattice

BRAVAIS LATTICE

Bravais showed that there are only 14 possible ways of arranging points in space such that the environment looks same from each point.

Thus, there are only 14 types of space lattices which are possibly developed from '7' crystal systems.

These 14 types of space lattices are known as Bravais lattices. The lattice can be primitive or non-primitive.

Primitive cell

A primitive cell is the simplest type of unit cell which contains only one lattice point per unit cell (contains lattice it cell (contains lattic points only at the corners of unit cell).

Example: Simple Cubic (SC), Simple Tetragonal

Non - primitive cell

The unit cell which contains more than one is called non- primitive cell.

Example: BCC, FCC and HCP contains more than one lattice point per unit cell.

If the number of lattice points per unit cell is two (BCC), three and four (FCC), then the unit cell is called doubly primitive, triply primitive and quadruply primitive respectively.

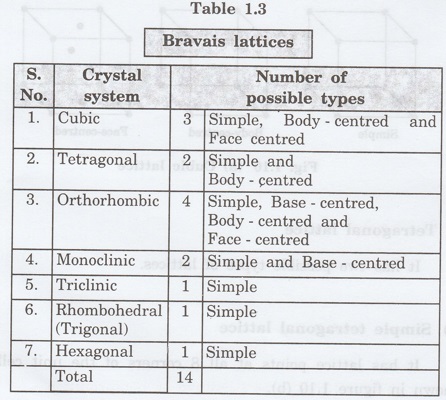
1. Cubic lattice

It has 3 possible types of arrangements of lattice points.

(i) Simple (or primitive) cubic lattice (SC)

It has lattice points at all 8 corners of the unit cell as shown in fig. 1.10 (a).

(ii) Body-centred cubic (bcc) lattice

It has lattice points at all 8 corners of the unit cell and one lattice point at the body centre as shown in fig. 1.10 (a).

(iii) Face - centred cubic (fcc) lattice

It has lattice points at all 8 corners of the unit cell and one lattice point at each face centre of 6 faces of the cube as shown in fig. 1.10 (a).

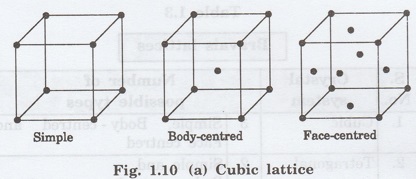
2. Tetragonal lattice

It has two possible types of lattices.

(i) Simple tetragonal lattice

It has lattice points at all 8 corners of the unit cell as shown in figure 1.10 (b).

(ii) Body-centred tetragonal lattice

It has lattice points at all 8 corners of the unit cell and one lattice point at the body centre as shown in fig. 1.10 (b).

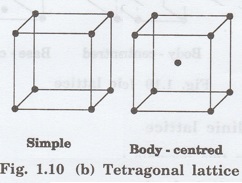
3. Orthorhombic lattice

It has four possible types of lattices.

(i) Simple orthorhombic lattice

It has lattice points at all 8 corners of the unit cell as shown in fig. 1.10 (c).

(ii) Body centred orthorhombic lattice

It has lattice points at all 8 corners of the unit cell and one lattice point at the body centre as shown in fig. 1.10 (c).

(iii) Face - centred orthorhombic lattice

It has lattice points at all 8 corners of the unit cell and one lattice point at each face centre of the 6 faces of the unit cell as shown in fig. 1.10 (c).

(iv) Base- centred orthorhombic lattice

It has lattice points at all 8 corners of the unit cell and 2 lattice points each at the centre of two faces (base) opposite to each other as shown in fig. 1.10 (c).

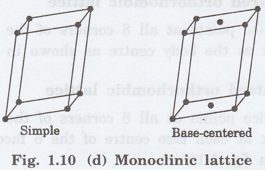
4. Monoclinic lattice

It has two possible space lattices.

(i) Simple monoclinic lattice

It has lattice points at all 8 corners of the unit cell as shown in fig. 1.10 (d)

(ii) Base - centred monoclinic lattice

It has lattice points at all 8 corners of the unit cell and 2 lattice points each at the centre of two faces (faces of the base) opposite to each other as shown in fig. 1.10 (d)

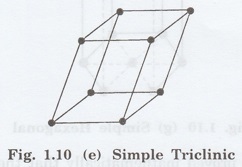
5. Triclinic lattice

It has only one possible space lattice.

Simple Triclinic lattice

It has lattice points at all 8 corners of the unit cell as shown in fig. 1.10 (e).

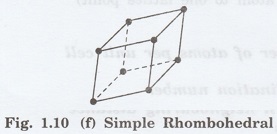
6. Rhombohedral lattice

It has only one possible space lattice.

Simple Rhombohedral lattice

It has lattice points at all 8 corners of the unit cell as shown in fig. 1.10 (f)

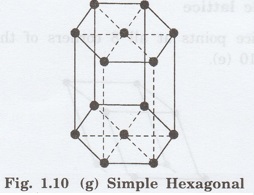
7. Hexagonal lattice

It has only one possible space lattice.

Simple Hexagonal lattice

It has lattice points at all 12 corners of the hexagonal unit cell and 2 lattice points each at the centre of two hexagonal faces of the unit cell (top and bottom) as shown in fig. 1.10 (g).

In fact, it is proved mathematically that there are only 14 independent ways of arranging points in three dimensional space such that each arrangement confirms to the definition of space lattice.

Characteristics of the unit cell

The unit cell is characterized by the following parameters: (Assuming one atom to one lattice point)

(i) Number of atoms per unit cell

(ii) Coordination number

(iii) Nearest neighbouring distance

(iv) Atomic radius

(v) Packing factor

(i) Number of atoms per unit cell

It is the number of atoms possessed by the unit cell. This is determined by the arrangement of atoms in the unit cell

(ii) Coordination Number (CN)

It is the number of nearest atoms directly surrounding a particular atom in a crystal.

The coordination number gives the information about the packing of atoms in a structure. It tells whether the crystal structure is closely packed or loosely packed.

If the coordination number is high, then the structure is more closely packed. If it is low, then the structure is loosely packed.

(iii) Nearest neighbouring distance (2r)

It is the distance between the centres of two nearest neighbouring atoms.

It is expressed in terms of the length of edge of the unit cell 'a' and it is 2r in simple cubic. (Fig. 1.11)

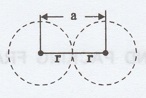
Fig. 1.11 Nearest neighbouring distances atomic radius

(iv) Atomic radius (r)

It is half of the distance between two nearest neighbouring atoms in a crystal. It is denoted by 'r'. It is usually expressed in terms of cube edge 'a' (lattice parameter).

For a simple cubic unit cell, the atomic radius. (Fig. 1.11).

r = a/2

(v) Packing Factor (PF)

It is defined as the ratio of total volume occupied by the atoms in a unit cell to the total volume of a unit cell.

Packing factor = Total volume occupied by the atoms in a unit cell (v) / Total volume of the unit cell (V)

= v / V

= Number of atoms per unit cell × Volume of one atom / Total volume of the unit cell

It is also known as density of packing.

The packing factor tells us how closely the atoms are stacked in the unit cell. A high packing factor indicates that atoms are very closely packed and therefore there is very little unoccupied space.

On the other hand, a low packing factor indicates loose packing of atoms and hence there is relatively more unoccupied space.