Body - Centred Cubic (BCC) Structure

BODY - CENTRED CUBIC (BCC) STRUCTURE

In this crystal structure, the unit cell has one atom at each corner of the cube and one atom at the body centre of the cube 1.16 (a). The atoms represented as hard spheres are shown in fig. 1.16 (b).

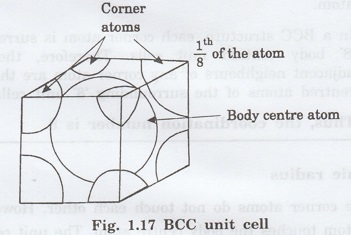
1. Number of atoms per unit cell

The unit cell of the BCC structure is shown in fig. 1.17.

Each corner atom is shared by 8 surrounding unit cells.

Hence, the share of one unit cell = (1/8) of corner atoms.

There are '8' corner atoms,

Contribution of all corner atoms = (1/8) × 8 = 1 atom

There is one atom at the body centre of each unit cell.

Total number of atoms in one unit cell = 1 + 1 = 2 atoms

2. Coordination number

In the unit cell of BCC structure, there is one atom (say atom X) at the body centre of the unit cell. There are '8' atoms at the 8 corners of the unit cell as shown in fig. 1.18.

The corner atoms do not touch each other. But all the eight corner atoms touch the body centre atom along the body diagonal. Thus, for body centre atom 'X', there are 8 nearest neighbours (ie., 8 corner atoms).

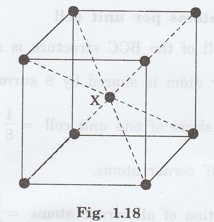
Hence, the coordination number of body centred cubic structure is 8.

Note: The coordination number can also be determined in another way by taking the corner atom as reference atom.

In a BCC structure, each corner atom is surrounded by '8' body centred unit cells. Therefore, the nearest adjacent neighbours of any corner atom are the '8' body centred atoms of the surrounding '8' unit cells.

Thus, the coordination number is 8.

3. Atomic radius

The corner atoms do not touch each other. However, each corner atom touches the body centre atom. The unit cell of BCC is shown in fig. 1.19. The side of the unit cell is 'a'.

Consider the atoms at A, G and at the centre of the unit cell 'O'.

It is clear from fig. 1.19 that the corner atoms A and G are nearest neighbouring atoms to the body centre atom O.

These atoms lie in a straight line along the body diagonal AG of the cube.

From the geometry of figure 1.19,

AG = r + 2r + r = 4r

on squaring on both sides, we get

AG² = (4r)²

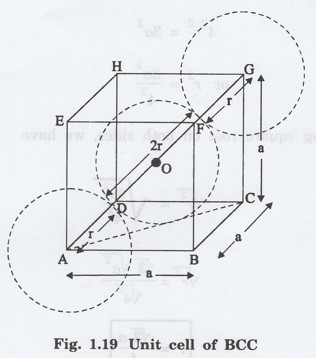
From the right angled ∆ ABC,

AC² = AB² + BC²

substituting for AB and BC from the fig 1.19, we have

AC² = a² + a²

AC² = 2a²

From the right angled ∆ ACG,

AG² = AC² + CG²

Substituting for AG², AC² and CG², we have

(4r)² = 2a² + a² = 3a²

4² r² = 3a²

Or r² = 3a²/4

Taking square root on both sides, we have

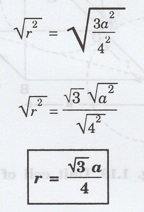
4. Packing factor

Number of atoms per unit cell = 2

Volume of 2 atoms in the unit cell, v = 2 x (4/3)πг3

Atomic radius r = √3 a/4

Volume of the unit cell, V = a³

Packing factor = v/V

Thus, packing factor is 68% ie., 68% of the volume of unit cell is occupied by atoms and the remaining 32% volume is vacant.

Common examples of this type of structure

Tungsten, Chromium and Molybdenum.