Anna University Solved Problems

ANNA UNIVERSITY SOLVED PROBLEMS

Problem 1.6

Lattice constant of a BCC crystal is 0.36 nm. Find its atomic radius. [A.U. Jan 2013]

Given data

a = 0.36 nm = 0.36 x 10^-9 m

Solution

For BCC, r = a√3 / 4

Substituting the given value, we have

 

Problem 1.7

Copper is FCC whose atomic radius is 1.26 x 10^-10 m. Calculate its lattice constant. (A.U. May 2012)

Given data

r = 1.26 x 10^-10 m.

Solution

For FCC, r = a √2 / 4

a = 4r / √2

substituting the given value, we have

a = (4 x 1.26 x 10^-10) / √2 m

a = 3.56 x 10^-10 m

a = 3.56 Å

 

Problem 1.8

Copper has a fcc structure and its atomic radius is 1.273 Å. Find (1) lattice parameter and (2) density of copper.

Atomic weight of copper = 63.5

Avagadro's number = 6.02 × 10²⁶ mol^–1 (A.U. Jan 2012)

Given data

Atomic radius for fcc system r = 1.273 Å = 1.273 x 10^-10 m

Atomic weight of copper M = 63.5

Avagadro's number N = 6.02 x 10²⁶ mol^-1

Number of atoms per unit cell n = 4

Solution

Lattice parameter a = 4r / √2

a = (4 x 1.273 x 10^-10) / 1.414

Lattice constant = 3.60 × 10^-10 m

We know that density p = nM / Na³

Substituting the given values, we have

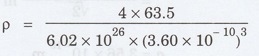
Density of copper p = 9043 kg m^-3

 

Problem 1.9

α - iron of atomic weight 55.85 solidifies into BCC structure and has a density 7860 kg m^-3. Calculate the radius of an atom. (A.U. Dec 2012)

Given data

Atomic weight M = 55.85

Density p = 7860 kg m^-3

Number of atoms per unit cell for BCC = 2

Avagadro's number N = 6.023 x 10²⁶ mol^-1

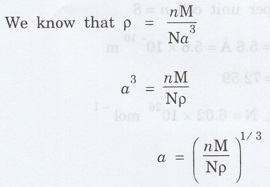
Problem 1.10

Ge crystallizes in diamond (form) structure with 8 atoms per unit cell. If the lattice constant is 5.6 Å Calculate its density. (A.U. May 2012)

Given data

Number of atoms per unit cell n = 8

Lattice constant a = 5.6 Å = 5.6 × 10^-10 m

Atomic weight, M = 72.59

Avagadro's number, N = 6.02 x 10²⁶ mol^-1

Solution

We know that p = nM / a³N

Substituting the given values, we have

 

Problem 1.11

Lithium crystallizes in BCC structure. Calculate the lattice constant, given that the atomic weight and density for lithium are 6.94 and 530 kg m³ respectively. (AU. Jan 2011)

Given Data

Atomic weight M = 6.94

Density p =530 kg m^-3

No. of atoms per unit cell for BCC, n = 2

Avagadro's number = 6.02 x 10²⁶ kg mol^-1

Solution

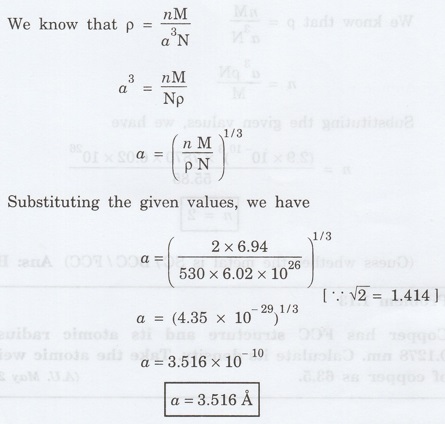
Problem 1.12

Calculate the number of atoms per unit cell of a metal with lattice parameter 2.9 Å. Given molecular weight 55.85, density 7870 kg m^-3 and Avagadro's number 6.02 x 10²⁶ mol^-1 (A.U. May 2012)

Given data

Lattice parameter a = 2.9 Å = 2.9 x 10^-10

Molecular weight = 55.85

Density p = 7870 kg m^-3

Avagadro's number, N = 6.02 x 10²⁶ mol^-1

Solution

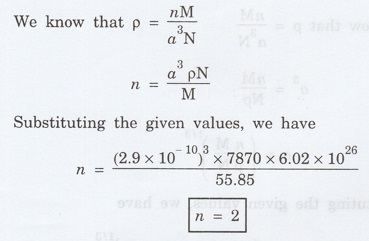
(Guess whether the metal is SC/BCC/FCC) Ans: BCC

Problem 1.13

Copper has FCC structure and its atomic radius is 0.1278 nm. Calculate its density. Take the atomic weight of copper as 63.5. (A.U. May 2011)

Given data

Atomic radius r = 0.1278 nm = 0.1278 × 10^-9 m

Atomic weight = 63.5

Avagadro's number N = 6.02 × 10²⁶ mol^-1

Number of atoms per unit cell for FCC, n = 4

Solution

We know that atomic radius for FCC

r = √2 a / 4

a = 4r / √2

substituting the given values, we have

Problem 1.14

Silicon has the same structure as diamond and a bond length of 0.2351 nm. Estimate its density.

(A.U. Jan 2010)

Given data

In the case of diamond cubic structure,

Bond length (2r) = 0.2351 nm = 0.2351 x 10^-9 m

Atomic radius (r) = 0.11755 × 10^-9 m

Number of atoms per unit cell (n) = 8 [diamond structure]

Atomic weight (M) for silicon = 28.09

Avagadro's number N = 6.02 × 10²⁶ mol^-1

Solution

Problem 1.15

Calculate the interplanar spacing of three important planes (100), (110) and (111) of a simple cubic system. (A.U. Jan 2013)

Solution

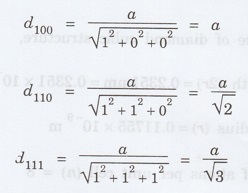
Problem 1.16

The distance between (110) plane in a BCC structure is 2.03 Å. What is the size of unit cell?

(A.U. Jan 2011)

Given data

d₁₁₀ = 2.03 Å

h = 1, k = 1, l = 0

Solution

Problem 1.17

Show that for a simple cubic system d₁₀₀: d₁₁₀: d₁₁₁: :√6: √3: √2 (A.U. Jan 2013)

Solution

Distance d between the adjacent planes is given by

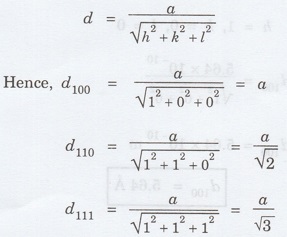
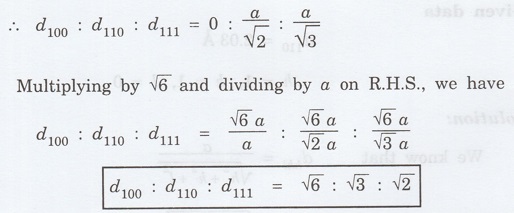
Problem 1.18

Determine spacing between (i) (100) planes (ii) (110) planes (iii) (111) planes in NaCl crystal having a lattice constant a = 5.64 Å. [A.U. April 2013]

Given data

Lattice constant a = 5.64 Å = 5.64 × 10^-10 m

Solution

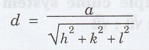
For [100] planes

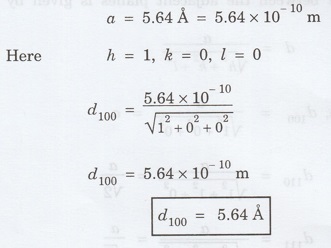
For [110] planes

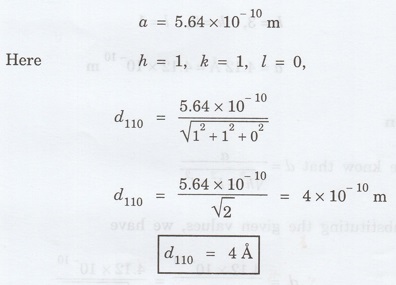
For [111] planes

Problem 1.19

Calculate the interplanar distance for (321) plane in simple cubic lattice with interatomic spacing equal to 4.12 Å. (A.U May 2012)

Given data

h = 3, k 2, l = 1

a = 4.12 Å = 4.12 × 10^-10 m

Solution

Substituting the given values, we have

 

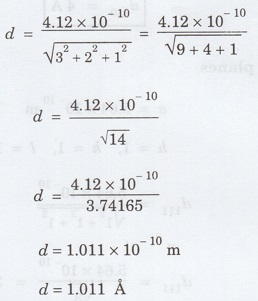
Problem 1.20

Lattice constant of copper is 0.38 nm. Calculate the distance between (110) planes. (A.U. Jan 2013)

Given data

a = 0.38 nm = 0.38 × 10^-9 m

h = 1 k = 1 l = 0

Solution

Substituting the given values, we have