Types of Negative Feedback Connections

TYPES OF NEGATIVE FEEDBACK CONNECTIONS

There are four different combinations

i. Voltage - series feedback

ii. Voltage - shunt feedback

iii. Current - series feedback

iv. Current - shunt feedback

The series feedback connections tend to increase the input resistance.

The shunt feedback connections tend to decrease the input resistance.

The voltage feedback tends to decrease the output resistance while the current feedback tends to increase the output resistance.

Decreased Distortion      

Consider an amplifier with an open loop voltage gain and a total harmonic distortion D.

Then with the introduction of negative feedback with the feedback ratio, β, the distortion will reduce to

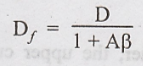
Decreased Noise:

There are many sources of noise in an amplifier depending upon the active device used with using the negative feedback ratio, β, the noise N can be reduced by a factor of 1/1+Aβ in a similar manner to non-linear distortion.

Thus the noise with feedback is given by

N_f = N / 1+Aβ

Increase in Input Impedance

An amplifier should have high input impedance so that it will not load the preceding stage or the input voltage source. Such a desirable characteristic can be achieved with the help of negative series voltage feedback. The input impedance with feedback is given by

Z_if = Z_i (1 + Aβ)

The input impedance is increased by the factor of (1 + Aβ)

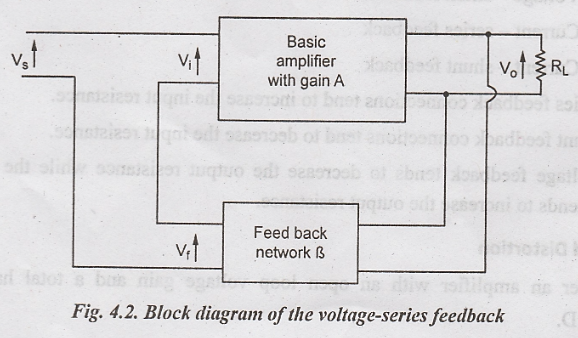
VOLTAGE SERIES FEEDBACK

A block diagram of a voltage-series feedback is shown in Fig.4.2.

The input to the feedback network is in parallel with the output of the amplifier. A fraction of the output voltage through the feedback network is applied in series with the input voltage of the amplifier. The shunt connection at the output reduces the output resistance R_o. The series connection at the input increases the input resistance. In this case, the amplifier is a true voltage amplifier.

The voltage feedback factor is given by β = V_f / V_o

Input and output Resistances

Fig. 4.3 shows the voltage series feedback circuit used to calculate input and output resistances.

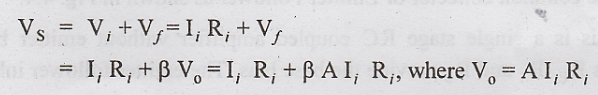
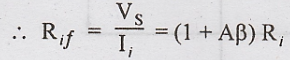
Hence the input resistance of a voltage series feedback amplifier is given by

R_if = (1 + Aβ) R_i

Where R_i - the input resistance of the amplifier without feedback.

For measuring the output resistance, R_L is disconnected and VS is set to zero. Then an external voltage V is applied across the output terminals and the current I delivered by V is calculated.

Then R_of = V/I. Due to feedback, input voltage V_f reduces output voltage A V_i which opposes V.

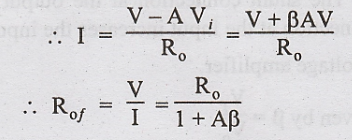
R_o - The output resistance of the amplifier without feedback.

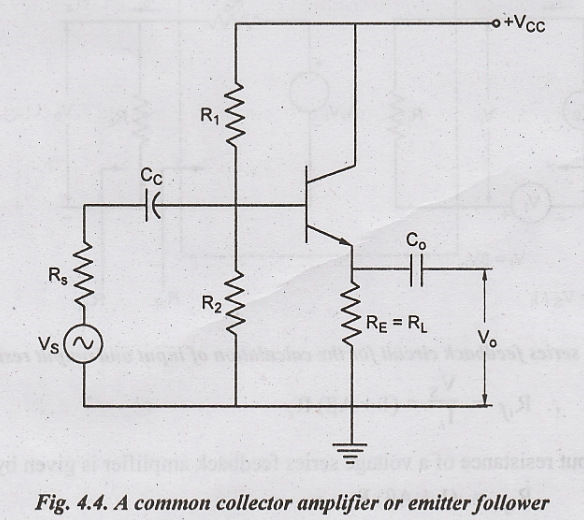
Emitter Follower

The common collector or Emitter Follower as shown in Fig. 4.4.

This is a single stage R_C coupled amplifier without emitter bypass capacitor across R_E. R₁ and R₂ provide the base bias. The emitter follower inherently exhibits 100% negative feedback since the voltage at the emitter follows the input voltage.

As the output voltage is taken across R_E = R_L, the feedback ratio, β = R_E/R_L = 1.

The overall voltage gain, A_f = A / 1 + A, which is little less than unity.

The emitter follower simultaneously increases input resistance and decrease output resistance characteristics of an emitter follower.

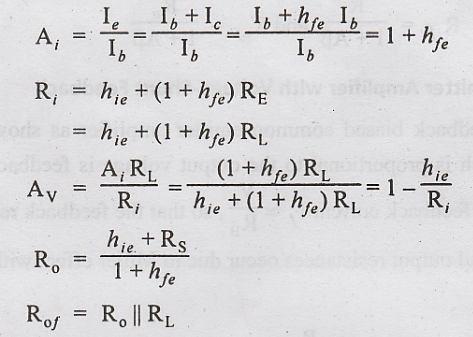
VOLTAGE SHUNT FEEDBACK

A voltage - shunt feedback is illustrated in Fig.4.5. It is called shunt- derived, Shunt-feedback connection. Here a fraction of output voltage is supplied in parallel with the input voltage through the feedback network.

The feedback signal If is proportional to the output voltage V_o. Therefore the feedback factor is given by β = I_f /V_o. This type of amplifier is called a trans-resistance

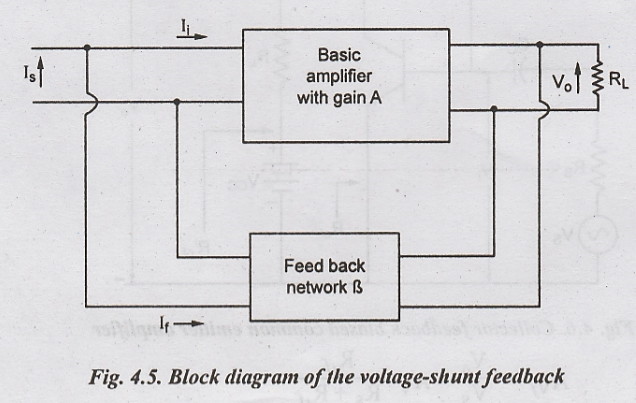
The voltage-shunt feedback provides a stabilized overall gain and decreases both input and output resistances by a factor (1 + Aβ).

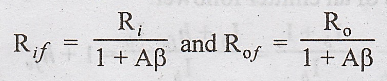
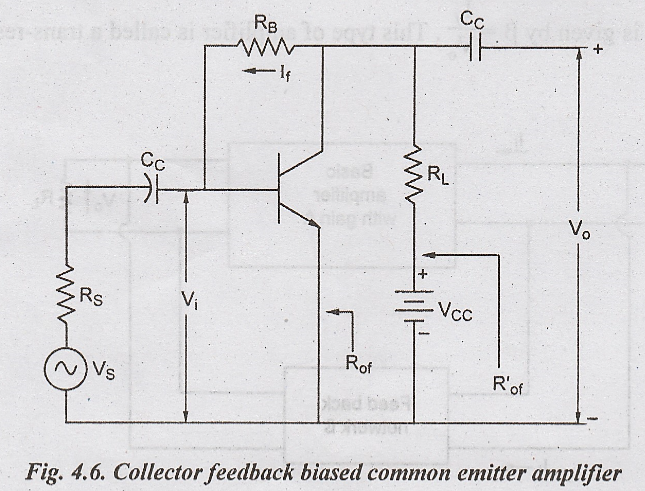
Common Emitter Amplifier with Voltage-Shunt Feedback

The collector feedback biased common emitter amplifier as shown in Fig. 4.6. Here a current which is proportional to the output voltage is feedback to the input.

Since V_o >> V_i, the feedback current I_f ≈ V_o/R_B, so that the feedback ratio β ≈ 1/R_B. The reduction in input and output resistances occur due to Miller effect with R_B.

Hence,

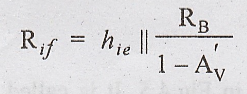
Where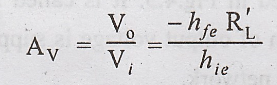 

and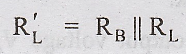 

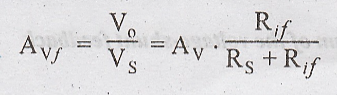
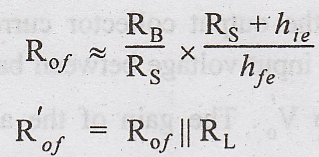
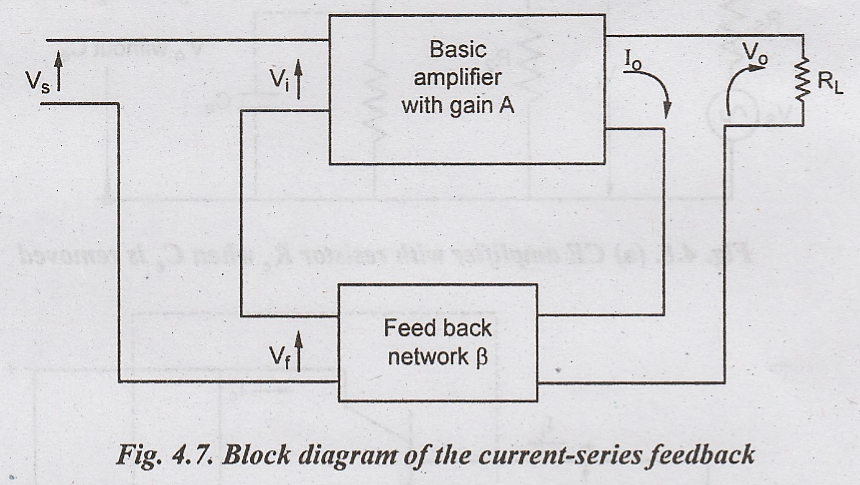
CURRENT-SERIES FEEDBACK

A block diagram of a current-series feedback is illustrated in Fig.4.7. In current- series feedback, a voltage is developed which is proportional to the output current because of the series connection at the input and output, the input and output resistances get increased.

This type of amplifier is called transconductance amplifier. The transconductance

feedback factor or ratio is given by β = V_f/I_o

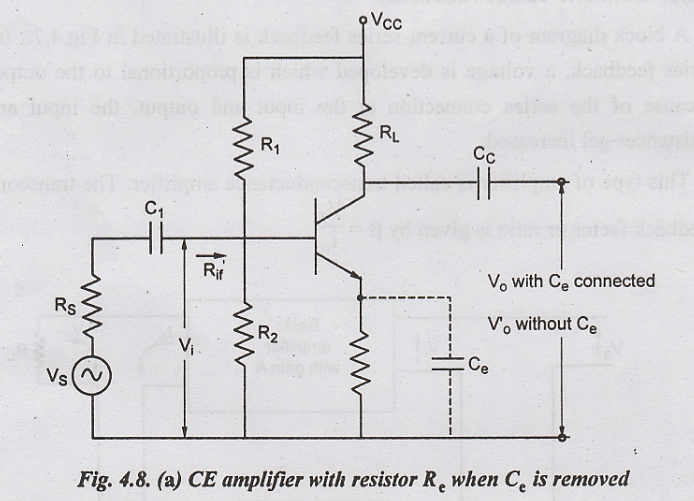
One of the most common methods of applying the current- series feedback is to place a resistor R_e between the emitter lead of a common emitter amplifier and ground. As the common emitter amplifier has a high gain, this is the most often used with series negative feedback so that it can afford to lose some gain. Such a circuit is illustrated in Fig.4.8.

When Re is properly bypassed with a large capacitor C_e, the output voltage is V_o and the voltage gain without feedback is A. Resistor R_e provides dc bias stabilization, but no an ac feedback when the capacitor C_e is removed an ac voltage will be developed across R_e due to the emitter current flowing through R_e and this

current is approximately equal to the output collector current. This voltage drop across R_e will serve to decrease the input voltage between base and emitter. So that the output voltage will decrease to V_o'. The gain of the amplifier with negative feedback is now A_f.

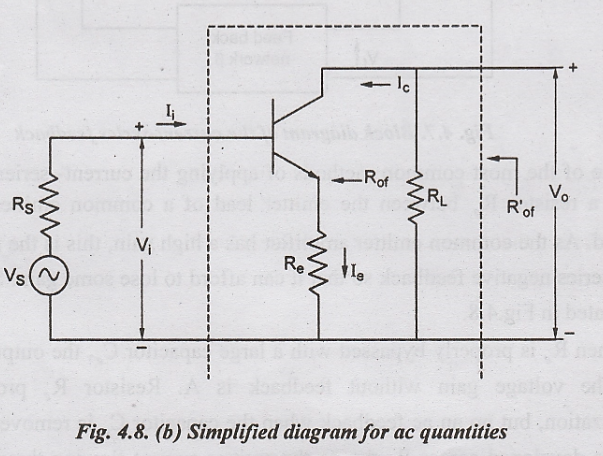
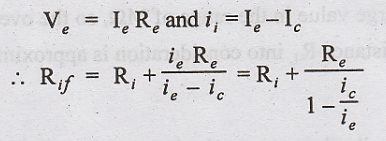
But we know that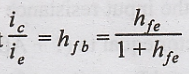 

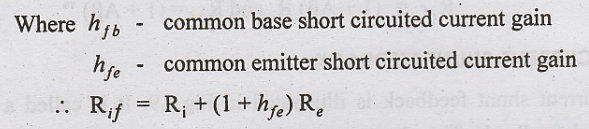
Thus, we find that there is a large increase in the value of input resistance due to negative feedback.

Input resistance without feedback, R_i = h_ie

R_if = h_ie + (1 + h_fe) R_e

If the bias resistance,  is considered the effective input resistance with feedback is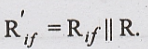 

Voltage gain (A_f)

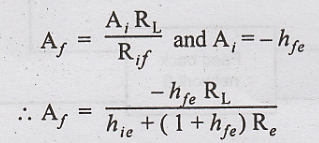
Voltage gain without feedback,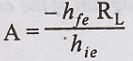

We find that there is a large decrease in voltage gain due to negative feedback.

Output Resistance (R_of)

The expression for the output resistance R_of looking back into the collector involves R_S, R_e and all the h-parameters. For values of R_e in the order of R_S and h_ie, an approximate expression for R_of is

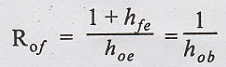
This has usually a large value in the range of MΩ, so the overall output resistance R'_of taking the load resistance R_L into consideration is approximately R_L.

Note:

The current series feedback increases the input resistance but decrease the output resistance of a feedback amplifier by a factor equal to (1 + Aβ). Thus,

R_if = (1 + Aβ) R_i and R_of = (1 + Aβ) R_o

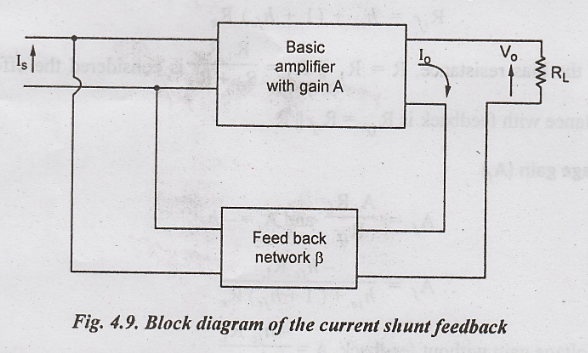
CURRENT-SHUNT FEEDBACK

A current shunt feedback is illustrated in Fig.4.9. It is called a series derived, shunt-fed feedback. The shunt connection at the input reduces the input resistance and the series connection at the output increases the output resistance. This is a true current amplifier. The current feedback factor is given by β = I_f/I_o

Input and Output Resistances

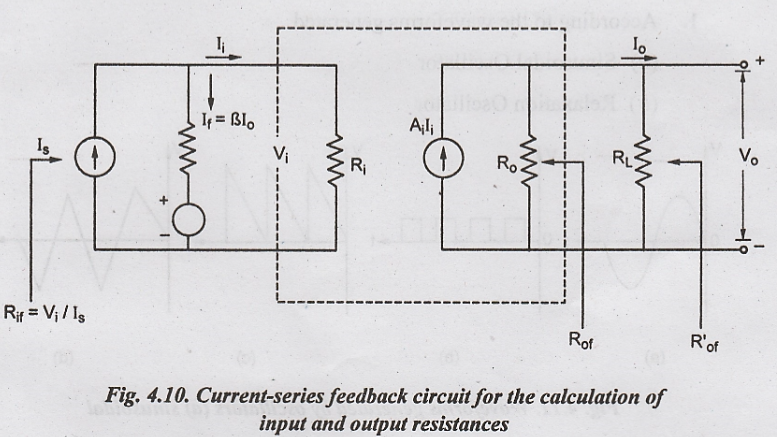
Fig.4.10 shows the current-shunt feedback circuit used to calculate input and output resistances

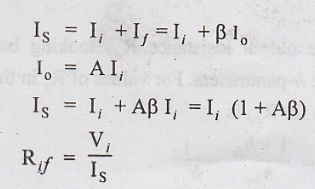
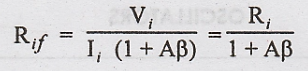
For measuring the output resistance, R_L is disconnected and V_S is set to zero. Then external voltage V is applied across the output terminals and the current I delivered by V is calculated.

Then R_of = V/I

with Is = 0, I_i = -I_f = -βI_o = βI. Since current in the output circuit due to feedback oppose the current I, due to applied voltage V.

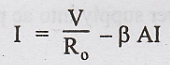
Simplifying this,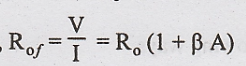 

Thus this type of feedback decreases the input resistance and increase the output resistance i.e.,

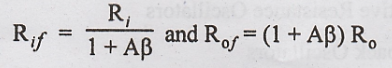
As this type of feedback has the least desirable effects, this connection will not be considered at all practical applications.