Electrical and Instrumentation Engineering: Unit II: DC Machines
Types of DC Motors
with Solved Example Problems
The types of DC motor: 1. Separately excited DC Motor 2. Self excited DC Motor
TYPES OF DC MOTORS
The
classification of DC motors is similar to that of the DC generator. The
classification is based on the connection of field winding in relation to the
armature. The types of DC motor:
1.
Separately excited DC Motor
2.
Self excited DC Motor
a.
Series Motor
b.
Shunt Motor
c.
Compound Motor
(i)
Long Shunt Compound Motor
(ii)
Short Shunt Compound Motor
Separately
Excited DC Motor
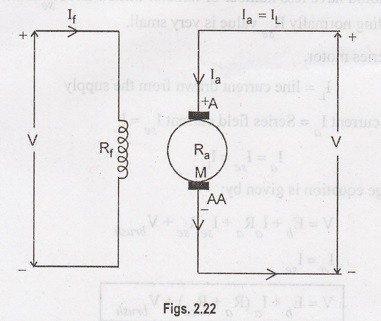
The
field winding and armature are separated. The field winding is excited by a
separate DC source. That is why it is called separately excited DC motor:
From
this diagram:
Armature
current Ia = Line current IL
Back
emf Eb = V – Ia Ra - Vbrush
Vbrush is very small and therefore is neglected.
Self
Excited DC Motor
DC Series Motor
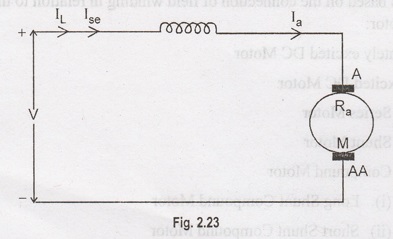
DC
series motor means, the field winding is connected in series with armature. The
field winding should have less number of turns of thick wire. Rse is
the resistance of the series field winding normally Rse value is
very small.
In
a DC series motor,
IL
= line current drawn from the supply
Armature
current Ia = Series field current Ise = IL
Ia
= Ise = IL
The
voltage equation is given by:
V
= Eb +Ia Ra + Ise Rse +Vbrush.
Ia
= Ise
V
= Eb +Ia (Ra+ Rse) +Vbrush
Vbrush
- Voltage drop in the brush.
Normally
it is neglected
V
=Eb +Ia (Ra+Rse)
In
a DC series motor, full armature current flows through the series field
winding, therefore flux produced is directly proportional to the armature
current.
φ
α Ise α Ia
DC Shunt Motor
In
a DC shunt motor, the field winding is connected across the armature.
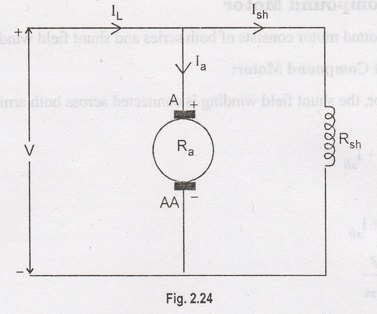
Here,
the shunt field winding has more number of turn with less cross-sectional area.
Rsh is the shunt field winding resistance. The value of Ra
is very small and Rsh is quite large. The input voltage V is equal
to the voltage across the armature and field winding.
It
is the line current drawn from the supply. The line current is divided into two
paths one through the field winding and second through the armature:
IL
=Ia + Ish
Ia
= armature current,
Ish
= shunt field current.
Ish
= V / Rsh
Voltage equation of DC shunt motor
V
= Eb +Ia Ra + Vbrush
In
shunt motor, flux produced by field winding is proportional to the field
current
φ
α Ish
Here,
the input voltage is constant and so that flux is also constant. Therefore DC
shunt motor is also called a constant flux motor or constant speed motor.
DC Compound Motor
A
DC compound motor consists of both series and shunt field windings.
(a) Long Shunt Compound Motor:
In
this motor, the shunt field winding is connected across both armature and
series field winding.
IL
= Ise + Ish
Ise
= Ia
IL
= Ia + Ish
Ish
= V / Rsh
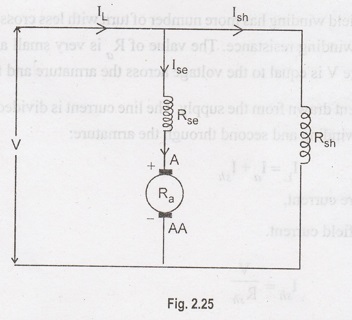
The
voltage equation of this motor is given by:
V
= Eb + Ia Ra + Ise Rse +
Vbrush
Ia
= Ise
V
= Eb + Ia (Ra + Rse) + Vbrush
(b) Short Shunt Compound Motor:
In
this type of motor, the shunt field winding is across the armature and series
field winding is connected in series with this combination.
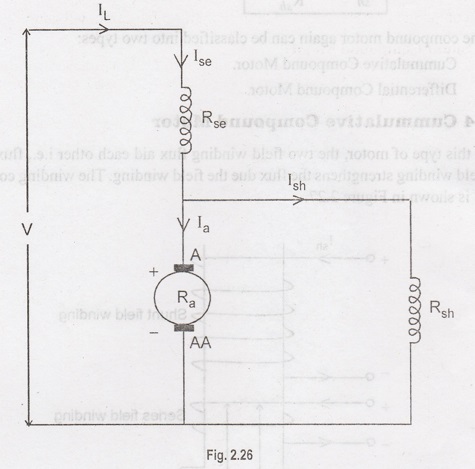
IL
= Ise
IL
= Ia + Ish
IL
= Ise = Ia + Ish
The
voltage across the shunt field winding can be found out from the voltage
equation:
V
= Eb + Ia Ra + Ise Rse +
Vbrush
Ise
= IL
V
= Eb + Ia Ra + IL Rse +
Vbrush
Voltage
drop across the shunt field winding = V – IL Rse
Vsh
= Eb + Ia Ra + Vbrush
Ish
= (V - IL Rse) / Rsh
The
compound motor again can be classified into two types:
1.
Cummulative Compound Motor.
2.
Differential Compound Motor.
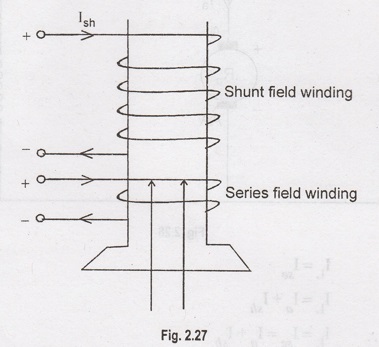
Cummulative Compound Motor
In
this type of motor, the two field winding flux aid each other i.e., flux due to
the series field winding strengthens the flux due the field winding. The
winding connection of diagram is shown in Figure 2.27.
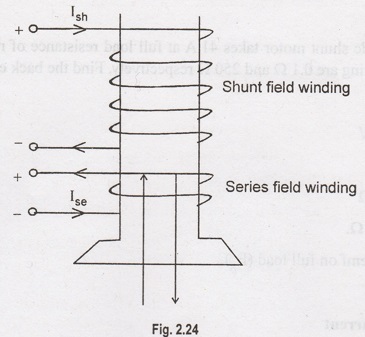
Differential Compound Motor
In
this type of motor, the two field winding flux oppose each other i.e., flux due
to series field winding weakens the field due to shunt field winding.
Example 2.1:
The
armature of a DC machine has a resistance of 0.1 Ω and is
connected to a 230 V supply. Calculate the back emf when it is running (i) as a
generator giving 80 A (ii) as a motor taking 80 A.
Given data:
Ra
= 0.1 Ω
Line
voltage V = 230 V.
To find:
Back
emf = ?
Solution:
(i)
As a generator giving 80 A
Induced
emf Eg = V + Ia Ra = 230 + 80 × 0.1
Eg
= 238 V.
(ii)
As a motor taking 80 A
Back
emf Eb = V - Ia Ra = 230 - 80 x 0.1
Eb
= 222 V.
Example 2.2:
A
250 V dc shunt motor takes 41 A at full load resistance of motor armature and
shunt field winding are 0.1 Ω and 250 Ω respectively. Find the back emf on full
load.
Given
data:
V
= 250 V
IL
= 41 A
Ra
= 0.1 Ω
Rsh
= 250 Ω.
To find:
Back emf on full load (Eb).
Solution:
Shunt Field Current
Ish
= V / Rsh = 250 / 250 = 1 A
Armature Current
Ia
= IL - Ish = 41 - 1 = 40 A
Back
emf Eb = V - Ia Ra = 250 - 40 × 0.1 = 246 V
Eb
= 246 V.
Example 2.3:
A
4 pole DC motor takes an armature current of 6 A. The armature has 480 lap
connected conductor. The flux per pole is 20 mwb. Calculate the gross torque
developed by the motor.
Given data:
Number
of poles P = 4
Armature
current Ia = 6 A
Number
of conductor Z = 480
Flux
per pole φ = 20 mwb
For
lap connection A = P.
To find:
Gross
torque (Ta).
Solution:
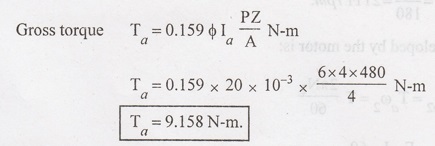
Example 2.4:
A
200 V, 2000 rpm, 10 A separately excited de motor has an armature resistance of
2 Ω. Rated de voltage is applied to both the armature and field winding of the
motor, if the armature draws 5 A from the source, calculate the torque
developed by the motor.
Given data:
Supply
Voltage V = 200 V
Motor
Speed N = 2000 rpm
Armature
resistance Ra = 2 Ω
Armature
Current Ia2 = 5 A
Armature Current Ia1 = 10 A
To find:
Torque
developed by the motor.
Solution:
Back
emf
Eb2
= V - Ia2 Ra = 200 - 5 x 2 = 190 V.
Back
emf
Ebl
= V - Ia1 Ra = 200 - 10 x 2 = 180 V.
Let
the motor speed be (N2) at armature current of 5 A.
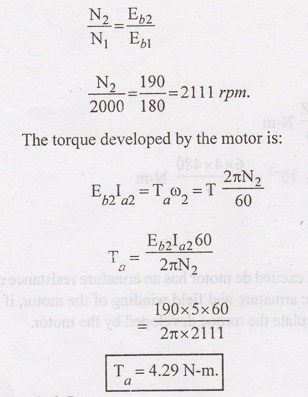
Example 2.5:
A
4 pole de motor is lap wound with 500 conductors. The pole shoe is 22 cm long
and the average flux density over one pole pitch is 0.4 T, the armature
diameter being 30 cm. Find the torque and gross mechanical power developed when
the motor is drawing 26 A and running at 1500 rpm.
Given Data:
No.
of poles P = 4
No.
of conductors Z = 500
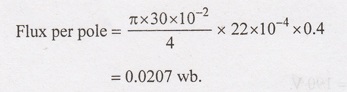
Armature
current Ia = 26 A
Motor
speed N = 1500 rpm
For
lap connection A = P.
To find:
(i)
Gross mechanical power.
(ii)
Torque developed.
Solution:

Example 2.6:
A
4 pole DC motor takes an armature current of 50 amps. The armature has 480 lap
connected conductor. The flux per pole is 20 mwb. Calculate the gross torque
developed by the motor.
Given data:
No.
of poles P = 4
Armature
current Ia = 50 A
No.
of conductor Z = 480
Flux
per pole φ = 20 × 10-3
For
lap connection A = P = 4.
To find:
Gross
torque developed by the motor (Ta).
Solution:
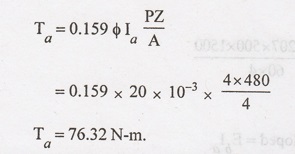
Electrical and Instrumentation Engineering: Unit II: DC Machines : Tag: : with Solved Example Problems - Types of DC Motors
Related Topics
Related Subjects
Electrical and Instrumentation Engineering
BE3254 - 2nd Semester - ECE Dept - 2021 Regulation | 2nd Semester ECE Dept 2021 Regulation
