The Adjoint of a Linear Operator

THE ADJOINT OF A LINEAR OPERATOR

Definition: Adjoint operator :

Let V(k) be an inner product space and T : V → V be linear operator.

Let  a unique operator T* on V such that <T(u), v> = <u, T*(v)> for all u, v Є V.

Then T* is called adjoint of T.

Note: T* is linear.

THEOREM 1.

Let V be a finite-dimensional inner product space over F, and let g : V → F be a linear transformation. Then there exists a unique vector y Є V such that g (x) = (x, y) for all x Є V

Proof :

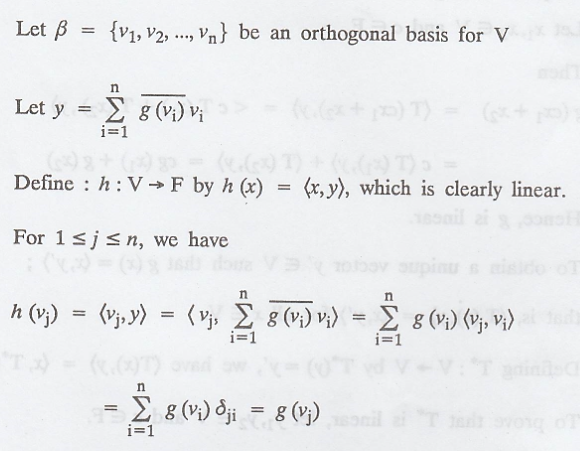
Since g and h both agree on β => g = h

Cor: To show that y is unique, suppose that g(x) = <x, y'> for all (x, y') for all x; Then <x, y'> so by Theorem 1, we have y = y'.

THEOREM 2.

Let V be a finite-dimensional inner product space, and let T be a linear operator on V. Then there exists a unique function. T* : V → V such that <T(x), y> = <x, T*(y)> for all x, y Є V. Furthermore, T* is linear.

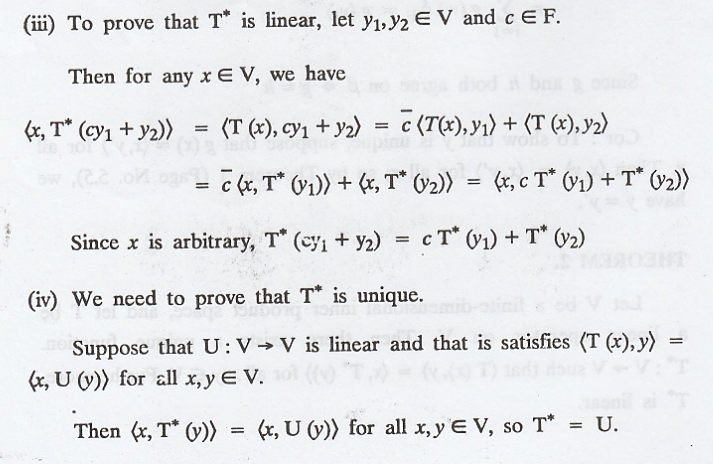
THEOREM 3.

Let V be a finite-dimensional inner product space, and let β be an orthonormal basis for V. If T is a linear operator on V, then

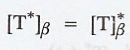
Proof :

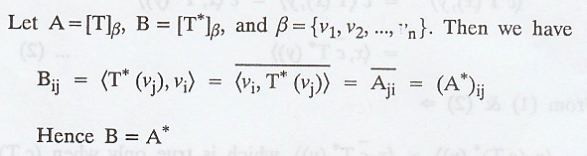
THEOREM 4.

Let V be an inner product space, and let T and U be linear operators on V. Then

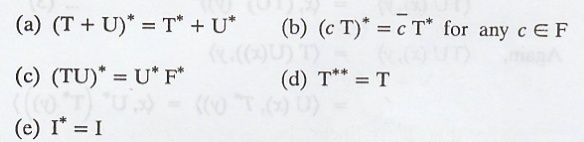
Solution :

T* + U* has the property unique to (T + U)*.

Hence T* + U* = (T + U)*

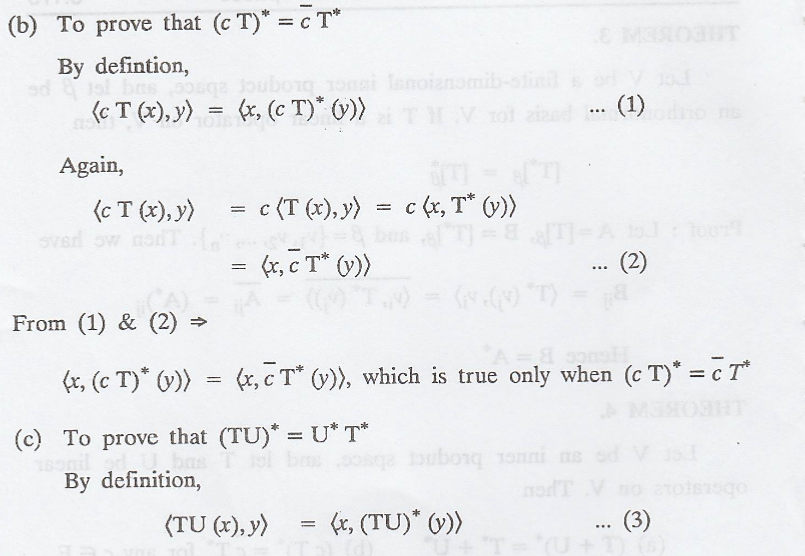
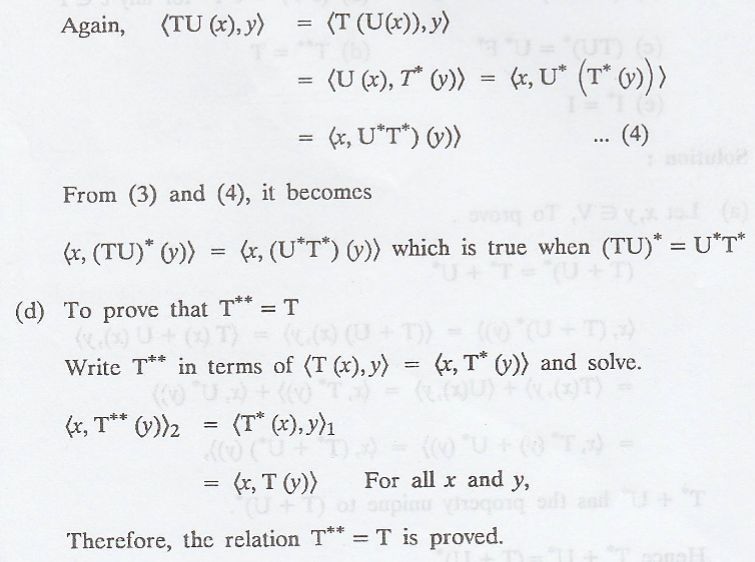
(e) To prove that I* = I

By definition,

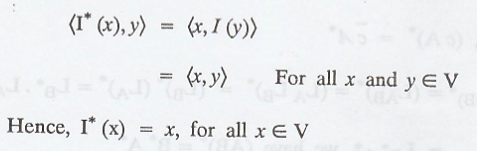
Therefore, the relation I* = I is proved.

Theorem 5 :

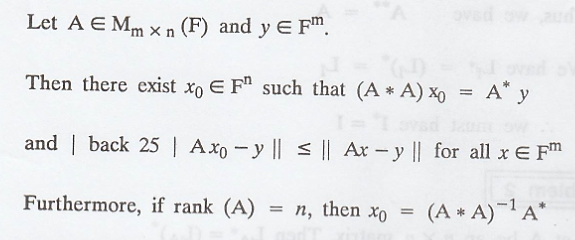
(a) The adjoint of a linear operator - matrices

Problem 1.

Let A and B be n x n matrices. Then

Proof :

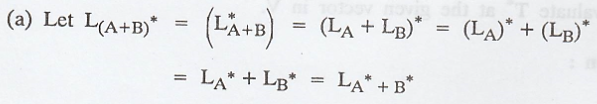
Problem 2

Let A be an n x n matrix. Then LA* = (LA)*

Proof :

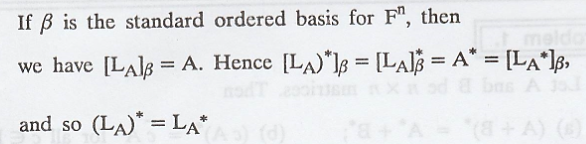
Problem 3.

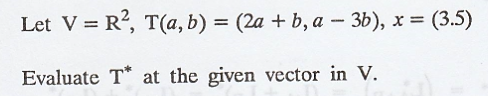
Solution :

Let α = {(1, 0), (0, 1)} be the standard basis for V = R²

Then, the standard matrix of T can be written as follows :

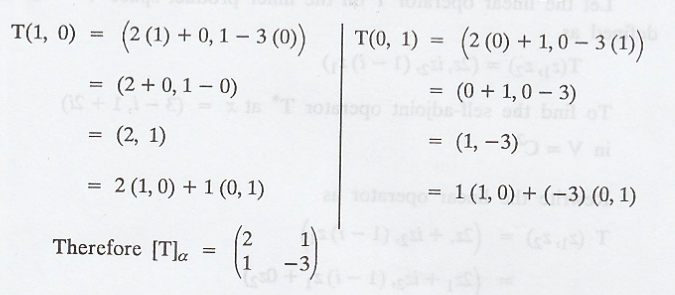
As the inner product space V = R² is real, so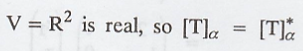

The self adjoint operator T* at x = (3, 5) is computed as,

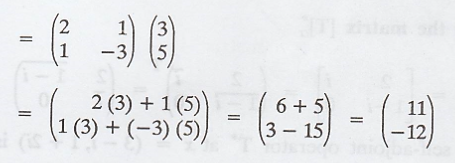
Therefore, the self-adjoint operator T* at x = (3, 5) is

T*(x) = (11, 12)

Problem 4.

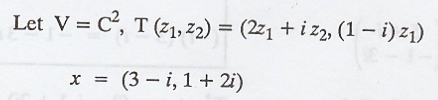
Evaluate T* at the given vector in V.

Solution :

Let the linear operator T on the inner product space V = C² is defined as,

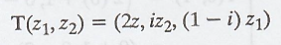
To find the self-adjoint operator T* at x = (3-i, 1+2i) in V = C²

Rewrite the linear operator as

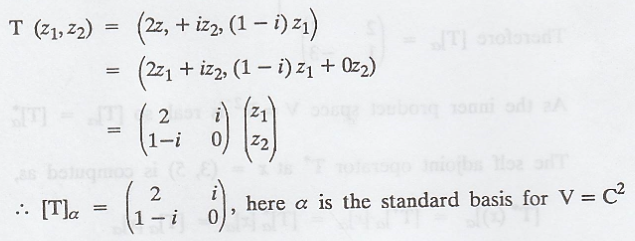
Find the matrix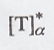 

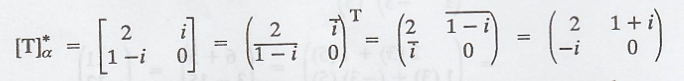
The self-adjoint operator T* at x = (3-i, 1+2i) is computed as,

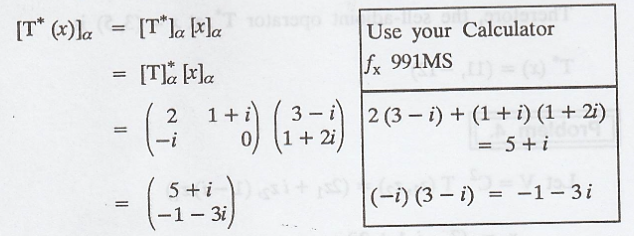
Therefore, the self-adjoint operator T* at x = (3-i, 1+2i) is,

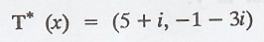
Problem 5.

Give an example of a linear operator T on an inner product space V such that N(T) ≠ N(T*)

Solution :

Let V be an inner product space

T : V → V be a linear operator.

To prove : N(T) ≠ N(T*)

Therefore, N(T) ≠ N(T*)

Problem 6.

Let T be a linear operator on a finite dimensional vector space V.

Prove that rank (T) = rank (T*)

Solution :

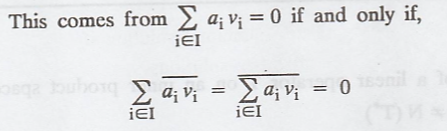
Let V be a finite-dimensional inner product space and let β be an orthonormal basis for V.

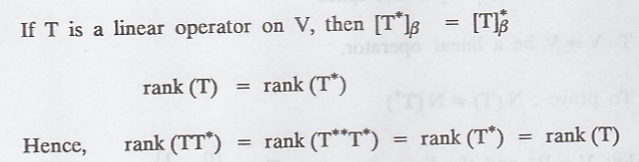
Problem 7.

Let T be a linear operator on a finite-dimensional vector space V. Prove that, for any n xn matrix A, rank (A*A) = rank (AA*) = rank(A)

Solution:

We know that

L_A*= (L_A)*. From this fact, apply the results obtained problem 9 & 10. The conclusion is, for any n x n matrix A, rank (A*A) = rank (AA*)

(b) Minimal solutions to Systems of Linear Equations

Even when a system of linear equations Ax = b is consistent, there may be no unique solution.

In such cases, it may be desirable to find a solution of minimal norm.

A solutions to Ax = b is called a minimal solution if ||s|| ≤ ||u|| for all other solutions u.

THEOREM 1.

Let A Є M_{m x n}(F) and b Є F^m. Suppose that Ax = b is consistent. Then the following statements are true.

(a) There exists exactly one minimal solution s of Ax = b, and s Є R(L_A*).

(b) The vector s is the only solution to Ax = b that lies in R(L_A*); that is if u satisfies (AA*)u = b, then s = A*u

Proof :

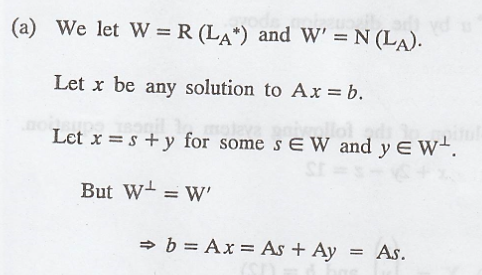
So s is a solution to Ax = b that lies in W.

To prove (a) To show that s is the unique minimal solution.

Let v be any solution to Ax = b.

We have that v = s + u, where u Є W'. Since s Є W, which equals 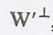, we have

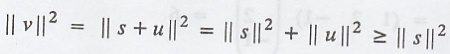
Hence, s is a minimal solution.

We can also see from the preceding calculation that if

||v|| = ||s||, then u = 0; hence v = s.

Therefore s is the unique minimal solution to Ax = b,

(b) Assume that v is also a solution to Ax = b that lies in W.

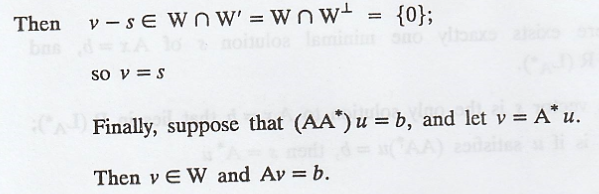
Therefore s = y = A*u by the discussion above.

Problem 1.

Find the minimal solution of the following system of linear equation.

x + 2y - z = 12

Solution :

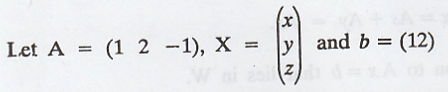
To find the minimal solution to the above system, find some solution u to AA* X = b.

Therefore, the minimal solution of the system Ax = b is given by A*u, where u is the solution of AA* X = b

Thus, the matrix AA* in invertible and hence,

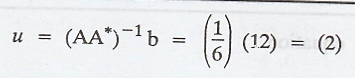
Therefore, the minimal solution is,

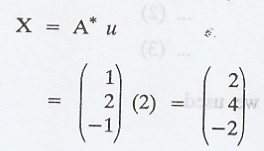
Hence, the minimal solution to the system is x=2, y = 4 and z = −2

Problem 2.

Find the minimal solution of the following system of linear equations :

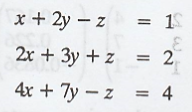
Solution :

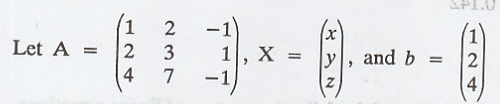
To find the minimal solution to the above system find some solution u to AA* X = b.

Therefore, the minimal solution of the system, AX = b is given by A*u, where u is the solution of AA*X = b

Now,

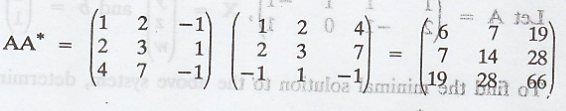
Consider system of equation

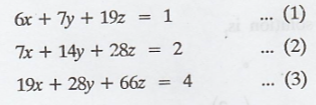
by using Gauss elimination we used

For which one solution is,

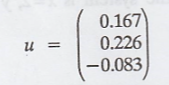
Therefore, the minimal solution is

X = A* u

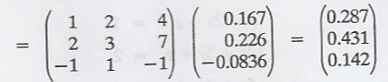
Thus, the minimal solution to the given system is x = 0.287, y = 0.431, and z = 0.142

Problem 3.

Find the minimal solution of the following system of linear equations.

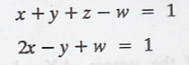
Solution :

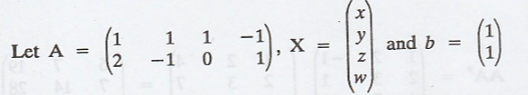
To find the minimal solution to the above system, determine some solution u to AA* X = b.

Therefore, the minimal solution of the system AX = b is given by A*u, where u is the solution of AA*X = b.

Now,

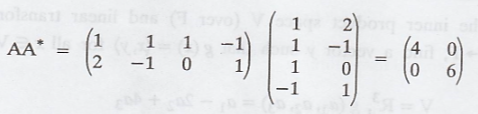
Thus, the matrix AA* is invertible and hence,

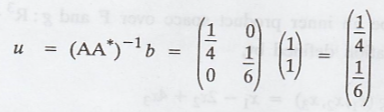
Therefore, the minimal solution is,

X = A* u

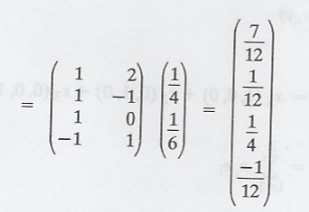
Thus, the minimal solution to the given system is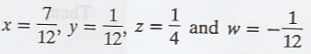 

(c) Linear operator on an inner product space

Problem 1.

The inner product space V (over F) and linear transformations g : V → F, find a vector y such that g(x) = (x, y) for all x Є V,

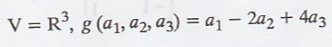
Solution :

Let V = R³ be an inner product space over F and g : R³ → F be a linear transformation defined by,

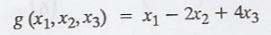
To find a vector y Є R³, such that g(x) = <x, y> for all x Є R³

Consider, g(x) = <x, y>

Here,

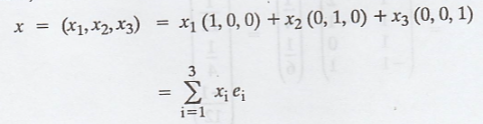
Then,

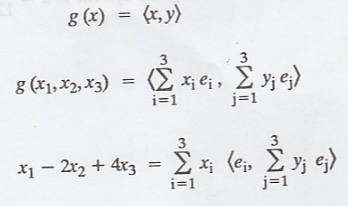
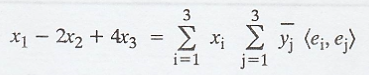
That is,

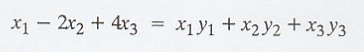
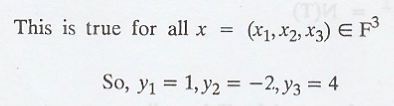
Therefore, the required vector is y = (1, -2, 4)

Problem 2.

Let T be a linear operator on an inner product space V. Let U₁ = T + T* and U₂ = TT*. Prove that U1 = U₁^* and U₂ = U₂^* 

Solution :

Let T be a linear operator on an inner product space V.

Let U₁ = T + T* and U₂ = TT*

To prove that U1 = U1* and U2 = U2* 

We know that,

Let V be an inner product space, and let T be linear operator on V then T** = T*

Thus,

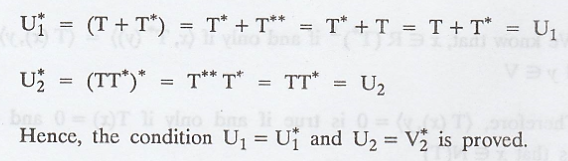
Problem 3.

Let V be an inner product space, and let T be a linear operator on V. Prove that

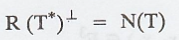
Solution :

Let V be an inner product, and let T be a linear operator on V.

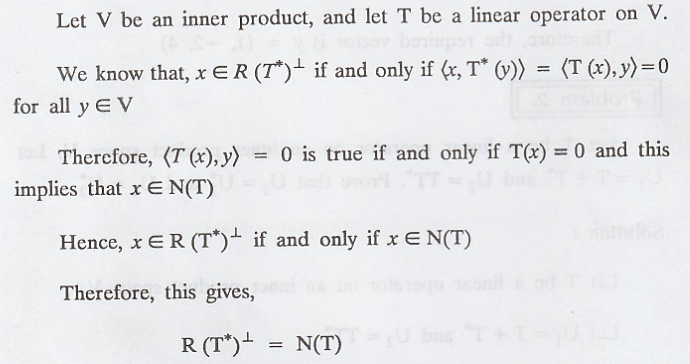
Problem 4.

Let V be an inner product space, and let T be a linear operator on V. Prove the following result.

If V is finite-dimensional, then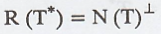 

Solution :

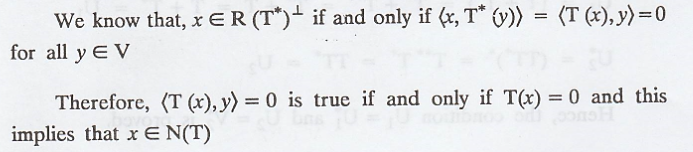
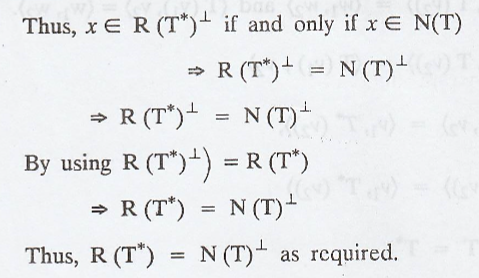
Problem 5.

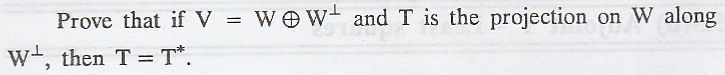
Solution :

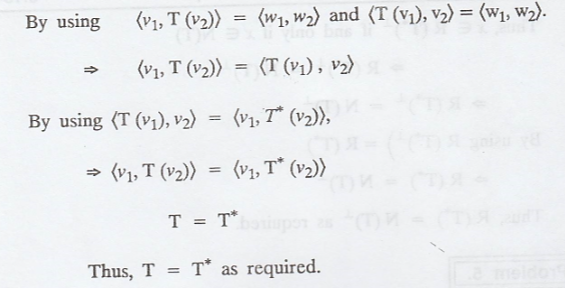
(d) Adjoint T - Least squares

Definition: Let T : V → W be a linear transformation, where V and W are finite-dimensional inner product spaces with inner products <.,.>₁ and <.,.>₂, respectively. A function T* : W → V is called an adjoint of T if <T(x), y>₂ = <x, T*(y)>₁ for all x Є V and y Є W.

Problem 1.

Let T : V → W be a linear transformation, where V and W are finite-dimensional inner product spaces with inner products <.,.>₁ and <.,.>₂, respectively. Prove the following result.

There is a unique adjoint T* of T, and T* is linear.

Solution :

T is linear and therefore the first component of inner product function is also linear.

In this case, we must have an unique vector T*, such that

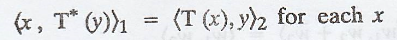
This means T*(y) is well defined.

Again, consider for all x and y.

By definition of an inner product, this implies that T* = U

Therefore, T* is unique.

To show that T* is linear.

By definition, we have

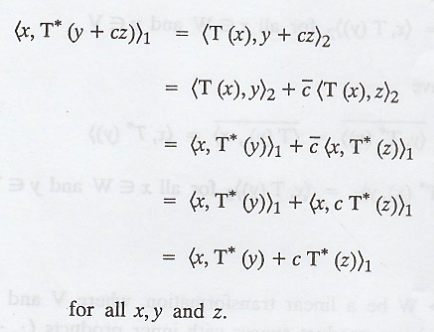
Problem 2.

Let T : V → W be a linear transformation, where V and W are finite-dimensional inner product spaces with inner products <.,.>₁ and <.,.>₂, respectively. Prove the following result.

rank (T*) = rank (T)

Solution :

Let V be a finite-dimensional inner product space.

Let β be an orthonormal basis for V.

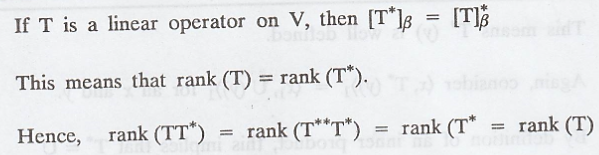
Problem 3.

Let T : V → W be a linear transformation, where V and W are finite-dimensional inner product spaces with inner products <.,.>₁ and <.,.>₂, respectively. Prove the following result.

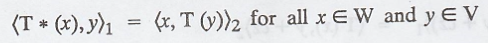
Solution:

We have

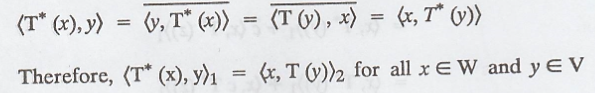
Problem 4.

Let T : V → W be a linear transformation, where V and W are finite-dimensional inner product spaces with inner products <.,.>₁ and <.,.>₂, respectively. Prove the following result.

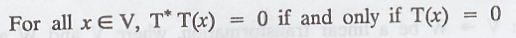
Solution :

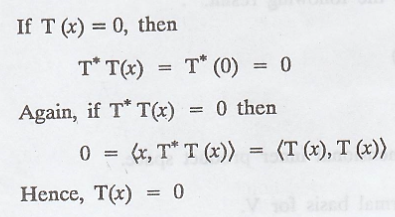
Problem 5.

Let V and {e₁, e₂, ...} defined as term of sequence e_n(k) = F_n,k where F_n.k is the Kroneckar delta.

Define T : V → V by

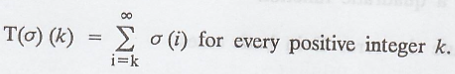
Notice that the infinite series in the definition of T converges because σ (i) ≠ 0 for only finitely many i.

Prove that T has no adjoint.

Solution :

Prove that T has no adjoint.

Use the method of contradiction to prove the given statement.

Assume that T* exist.

Now, observe that

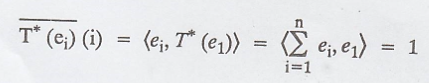
This is not possible since T*(e1) is not an element in V.

Therefore, the operator T has no adjoint.

EXERCISE 5.5

For each of the sets of data that follows, use the least squares approximation to find the best fits with both

(i) a linear function and

(ii) a quadratic function

Compute the error E in both cases.

(a) {(1, 2), (3, 4), (5, 7), (7, 9), (9, 12)}

(b) {(-2, 4), (-1,3), (0, 1), (1, −1), (2, −3)}

2. Find the minimal solution to each of the following system of linear equations.

(a) x + y - z = 0

(b) x + y - z = 0; 2x - y + z = 3; x - y + z = 2

3. A linear operator on R² is defined by T(x,y) = (x + 2y, x − y) Find the adjoint, i.e., T* if the inner product is standard one. If α = (1,3), find T*(α)