Inner Product spaces - Parseval's identity - Bessele's Inequality

(e) Inner product spaces - Parseval's identity - Bessele's inequality

Problem 1.

Let V be a finite-dimensional inner product space over F.

(a) Parseval's Identity. Let = {v₁, v₂, ..., v_n} be an orthonormal basis for V. For any x, y Є V prove that

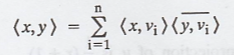
(b) Use (a) to prove that if β is an orthonormal basis for V with inner product <.,.>, then for any x, y Є V

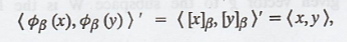
where <.,.>' is the standard inner product on Fⁿ.

Solution :

Let V is the finite-dimensional inner product space over F.

(a) Let {v₁, v₂, ..., v_n} be an orthonormal basis for V.

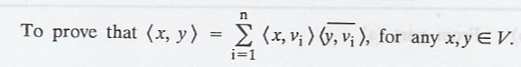
We know that, property of inner product space,

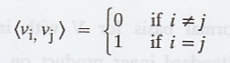
Use the above property, and for any j

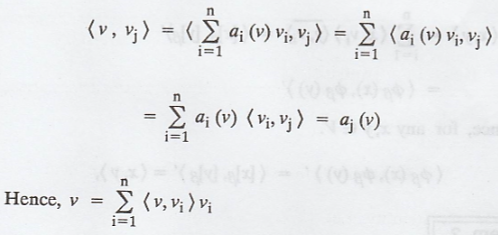
Since V has an orthonormal basis and for any x, y Є V, then

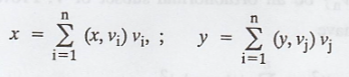
Let the inner product <x,y>

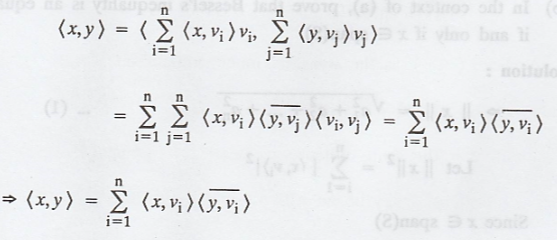
(b) From part (a)

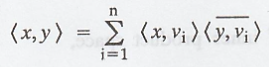
Suppose β is an orthonormal basis for V with inner product <.,.>, where <.,.>' is the standard inner product on Fⁿ

Then for any x, y Є V

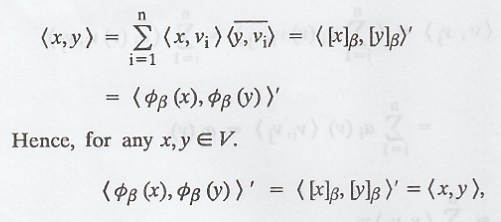
Hence, for any x, y Є V.

Problem 2.

(a) Bassel's Inequality. Let V be an inner product space, and let {v₁, v₂, ..., v_n} be an orthonormal subset of V. Prove that for any x Є V we have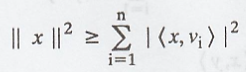 

(b) In the context of (a), prove that Bessel's inequality is an equality if and only if x Є span(S).

Solution :

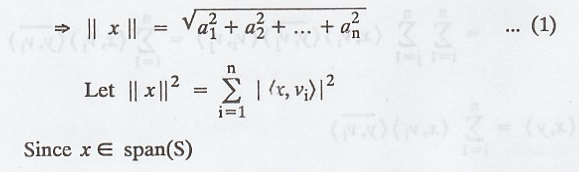
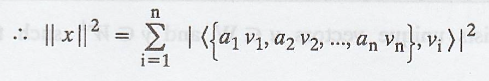
As,

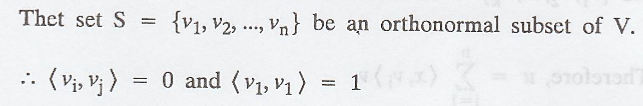
Hence,

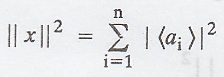
From (1), equality holds

.'. Bassel's inequality is equality if and only if x Є span(S)

Hence the proof.

(a) Let V be an inner product space

And S = {v₁, v₂, ..., v_n} be an orthonormal subset of V.

To prove that for any x Є V

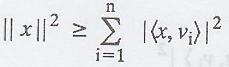
Let W = span(S).

Here, W is a finite diminished subspace of V.

Since x Є V, x can be written as x = u + y, where u Є W and y Є W

Given : S is an orthonormal basis of W.

"As W is a finite dimmensional subspace of an inner product space V and let x Є V

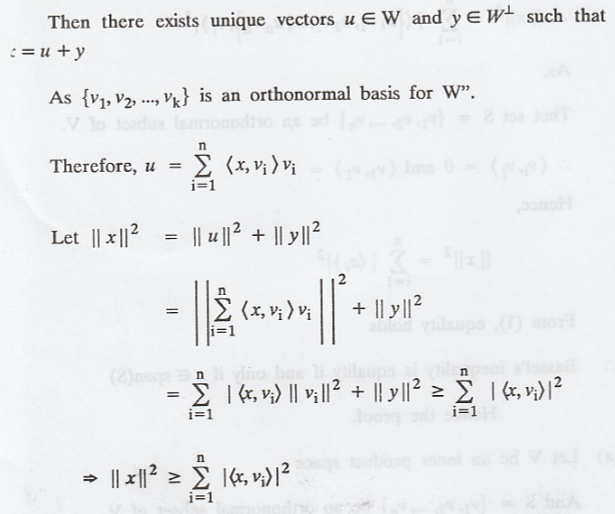
(b) To prove that Bessel's inequality is equality if and only if x Є span(S)

Bessel's equality is,

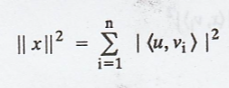
Thus x can be written as,

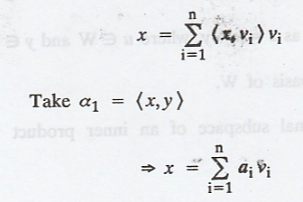
i.e., x can be written as a linear combination of S = {v₁, v₂, ..., v_n}

Thus x Є span(S)

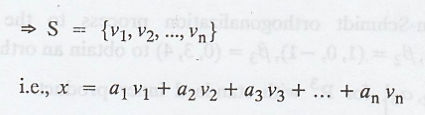
EXERCISE 5.4

1. In each part, apply the Gram-Schmidt process to the given subset S of the inner product space V to obtain an orthogonal basis for span(S). Then normalize the vectors in this basis to obtain an orthonormal basis β for span(S), and compute the Fourier coefficients of the given vector relative to β.

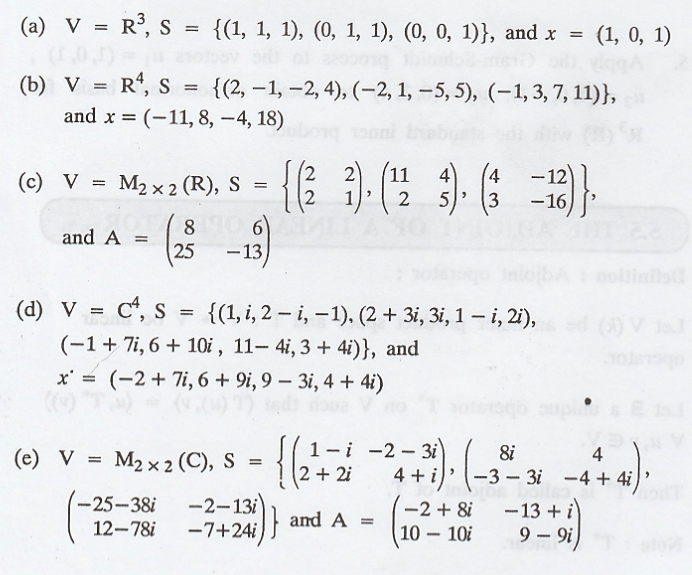
2. Linear Transformation and Inner Product Spaces Let W be a subspace of the linear product space V spanned by (0, 1, 1, 0), (0, 5, -3, -2), (-3, -3, 5, -7) find an orthonormal basis for W.

3. Apply Gram-Schmidt orthogonalization process to the vectors β₁ = (1, 0, 1), β₂ = (1, 0, -1), β₃ = (0, 3, 4) to obtain an orthonormal basis {α₁, α₂, α₃} for R³ with standard inner product.

4. If S is a subset of an inner product space, then prove that

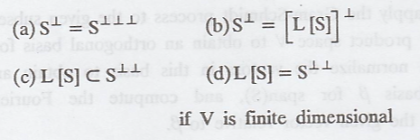
5. Apply the Gram-Schmidt process to the vectors u₁ = (1, 0, 1), u₂ = (1, 0, -1), u₃ = (0, 3, 4) to obtain orthonormal basis for R³(R) with the standard inner product.