Solved Example Problems of DC Machines

EXAMPLES

1. Calculate the emf generated by a 6 pole DC generator having 480 conductors and driven at a speed of 1200 rpm. The flux per pole is 0.012 Wb. Assume the generator to be (a) Lap wound, (b) Wave wound.

Solution:

2. A wave connected armature winding has 19 slots with 54 conductors per slot. If the flux per pole is 0.025 Wb and number of poles is 8, find the speed at which the generator should be run to give 513 V. Also find the speed if the armature is lap connected.

Solution:

P = 8

φ = 0.025 Wb

Z = 19 × 54 = 1026

A = 2 (for wave)

E_g = 513 Volts

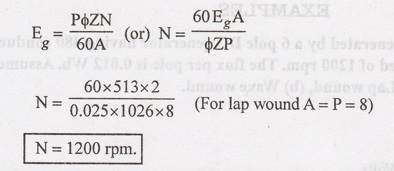
3. The armature of a 4-pole, 600 rpm, lap wound generator has 100 slots. If each coil has 4 turns, calculate the flux per pole required to generate an emf of 300 V.

Solution:

No. of poles = 4; Speed 600 rpm,

No. of slots = 100; E_g = 300 V

No. of conductors Z = 100 × 4 × 2=8

Lap wound generator, A = P = 4

4. A 6-pole, lap wound armature rotated at 350 rpm is required to generate 300 V. The useful flux per poles is 0.05 Wb. If the armature has 120 slots; calculate the no. of conductors per slot.

Solution:

Given data:

No. of Poles, P = 6

Speed N = 350 rpm

E_g = 300 V

Flux / Pole = 0.05 Wb

No. of Slots = 120.

For lap wound generator, A = P = 6.

To find:

No. of conductors / slot.

Solution:

No. of conductors / slot = 1029/120 = 8.575

Conductors / Slot = 9.

5. A 50 kW, 250 V shunt generator operates on full load at 1500 rpm. The armature has 6 poles and is lap wound with 200 turns. Find the induced emf and the flux / pole at full load. Given that the armature and field resistances are 0.01 and 125 Ω respectively. Neglect armature reaction.

Solution:

For a load power of 50 kW at a terminal voltage of 250 V, load current.

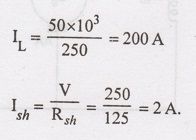
6. A 4-pole lap connected shunt generator has R_sh = 100 Ω and R_a =0.1 Ω and supplies sixty lamps each rated 40 W 200 V. Calculate the armature current, induced emf and current in each parallel path of the armature. Allow a brush drop of 1 V per brush.

Solution:

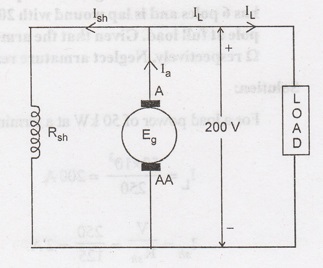
Armature current

I_a = I_L + I_sh = 12 + 2 =14A

No. of parallel paths = No. of poles = 4 (lap)

Current / Path = 14 / 4 = 3.5 A

Induced emf E_g = V + I_a R_a + brush drop = 200 + 14 x 0.1+2 x 1

E_g = 203.4 Volts.

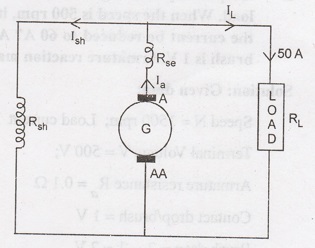
7. A compound generator delivers a load current of 50 A at 500 V. The resistances are R_a = 0.05 Ω, R_se = 0.03 Ω and R_sh = 250 Ω. Find the induced emf, if contact drop is 1 V per brush. Neglect armature reaction. Assume (a) Long Shunt (b) Short Shunt Connection.

Solution: Long Shunt Connection:

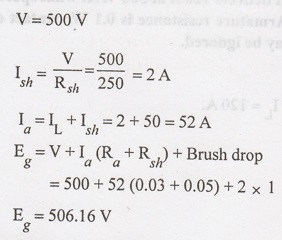
Short Shunt Connection:

Now the shunt field current is obtained by dividing (V + I_L R_se) by the shunt field resistance.

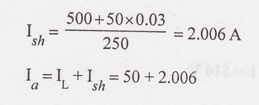
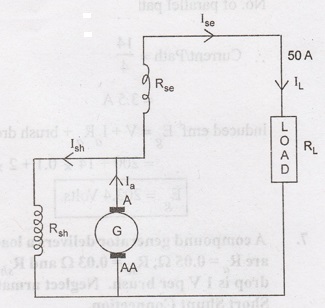
8. A separately excited generator with constant excitation is connected to a constant load. When the speed is 500 rpm, it delivers 120 A at 500 V. At what speed will the current be reduced to 60 A? Armature resistance is 0.1 W, contact drop/ brush is 1 V. Armature reaction may be ignored.

Solution: Given data:

Speed N = 1500 rpm; Load current I_L = 120 A.

Terminal Voltage V = 500 V;

Armature resistance R_a = 0.1 Ω

Contact drop / brush = 1 V

Brush drop = 2 x 1 = 2 V.

To find:

Motor speed N at 60 A.

Solution:

E_g1 = V + I_a1 R_a = V_brush = 500 + 120 x 0.1 + 2 x 1 = 514 V

N₁ = 1500 rpm

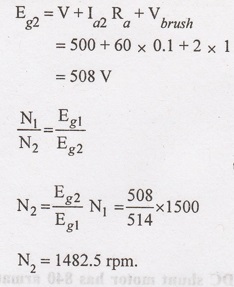
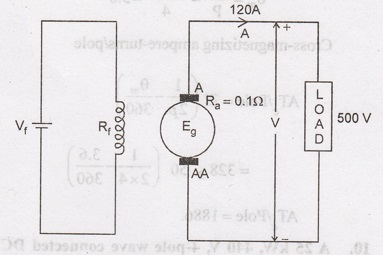
9. A 250 V, 25 kW, 4-pole DC generator has 328 wave connected armature conductors. When the machine is delivering full load, the brushes are given a lead of 7.2 electrical degrees. Calculate the cross magnetizing amp-turns/pole.

Solution: Given data:

Terminal Voltage V = 250 V

Output Power P_out = 25 kW

No. of Poles P = 4

No. of conductors Z = 328

θ_e = 7.2°

Wave connected A = 2.

To find:

Cross-magnetising ampere-turns/pole.

Solution:

Load current supplied

I_a = (25 × 1000) / 250 = 100A

I = 100 / A = 100 / 2 = 50A (current/path)

10. A 25 kW, 440 V, 4-pole wave connected DC shunt motor has 840 armature conductors and 140 commutator segments. Its full-load efficiency is 88% and the shunt field current is 2 A. If brushes are shifted backwards through 1.5 segments from the geometrical neutral axis, find the demagnetizing and distorting amp-turns/pole.

Solution: Given data:

Motor output power = 25 kW; Supply Voltage = 440 V.

No. of poles P = 4; No. of conductors Z = 840;

Full-load efficiency = 88% = 0.88

Shunt field current I_sh = 2 A

No. of commutator segments = 140.

To find:

Demagnetizing and distorting ampere-turns/pole.

Solution:

Motor input power = Motor output / Efficiency = 25000 / 0.88 = 28409 W.

Motor input current I_L = 28409 / 440 = 64.56 A.

Shunt field current I_sh = 2 A

Armature current I_a = 64.56 - 2 = 62.56 A

Current in each conductor I = I_a / 2 = 62.56 / 2 = 31.28 A.

θ_m = (1.5 × 360) / 140 = 3.85°.

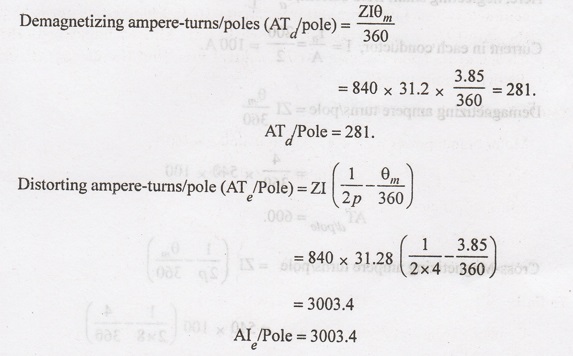
11. A wave connected 8-pole, 60 kW, 300 V DC generator has 540 conductors and delivers full load current. If the brush shift is 4^o (mechanical), calculate demagnetizing and cross magnetizing AT/Pole

Solution:

Given data:

For wave connected A = 2; Terminal voltage V = 300 V.

No. of poles P = 8; No. of conductors Z = 540.

Output Power P_out = 60 kW; θ_m = 4^o.

To find:

Demagnetizing AT/Pole

Cross Magnetising AT/Pole.

Solution:

Load Current Supplied I_L = 6 x 10³ / 300 = 200 A.

Here, neglecting shunt field current, I_a = I_L = 200 A.

Current in each conductor, I = I_a / A = 200 / 2 = 100A

12. Determine per pole the number:

(i) Of cross-magnetizing ampere-turns

(ii) Of back ampere-turns and

(iii) Of series turns to balance the ampere-turns in the case of a DC generator having the following data: 500 conductors, total current 100 A, 4 poles, 2-circuit wave winding, angle of lead= 10°, leakage co-efficient = 1.3.

Solution:

Given data:

No. of conductors Z = 500

Total Current I_a = 100 A

No. of poles P = 4; Angle of lead θ_m = 10°

For wave connected, A=2; Leakage co-efficient λ = 1.3.

To find:

Cross magnetizing ampere turns (AT_c /Pole)

Back ampere-turns (AT_d/Pole)

No. of series turns to balance the back ampere-turns.

Solution:

13. A 4-pole DC motor takes an armature current of 6 A. The armature has 480 lap connected conductors. The flux per pole is 20 mWb. Calculate the gross torque developed by the motor.

Solution:

P = 4

I_a = 6 A

Z = 480

φ = 20 mWb

A = P

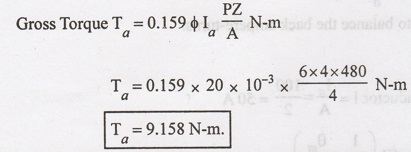
14. A 4 pole DC motor takes an armature current of 50 A. The armature has 480 lap connected conductors. The flux per pole is 20 mWb. Calculate the gross torque developed by the motor.

Solution:

No. of poles P = 4

Armature current I_a = 50 A

No. of conductors Z = 480

φ =20 × 10^-3

Lap connection A = P = 4.

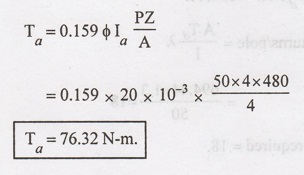
15. A 200 V, 2000 rpm, 10 A separately excited DC motor has an armature resistance of 2 Ω. Rated DC voltage is applied to the armature and field winding of the motor. If the armature draws 5 A from the source, calculate the torque developed by the motor.

Solution:

V = 200 V; Motor Speed N = 2000 rpm, R=2 Ω

Armature current I_a2 = 5 A, I_al = 10A

Back Emf E_b2 =V - I_a2 R_a = 200 - 5 x 2 = 190 V

E_b1 = V - I_al R_a = 200 - 10 x 2 = 180 V