Solved Example Problems of AC Rotating Machines

PROBLEMS

1. A squirrel cage induction motor has a slip of 4% at full load. Its starting current is fine times the full load current. The stator impedance and magnetizing current may be neglected; the rotor resistance is assumed constant.

(a) Calculate the maximum torque and the slip at which it would occur.

(b) Calculate the starting torque.

Express torque in Pu of the full load torque.

Solution:

Dividing Equation (1) by (2)

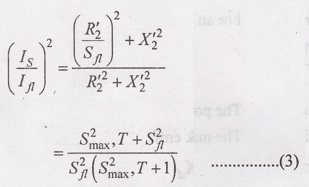
Substituting the values

(or) S_max, T = 0.2 (or) 20%

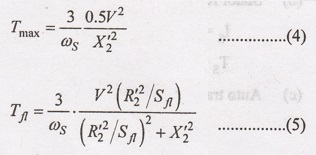
Div. equation (4) by (5)

(or) T_max = 2.6 Pu

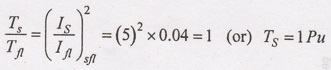
2. A small squirrel cage induction motor has a starting current of six times the full load current and a full-load slip of 0.05. Find in Pu of full load values, the current (line) and starting torque with the following methods of starting ((a) to (d)).

(a) Direct startup

(b) Stator resistance startup with motor current limited to 2 Pu

(c) Auto Transformer starting with motor current limited to 2 Pu and

(d) Star-delta starting

(e) What auto transformer ratio would sign 1 pu starting torque?

Solution:

(a) Direct Switching

I_S = 6 Pu

T_S = (6)² × 0.05 = 1.8

(b) Stator resistance starting

I_S = 2 (Pu) (limited to)

T_S = (2)² × 0.05 = 0.2 Pu

(c) Auto transformer starting

X = 2/6 = 1/3

I_S(motor) = 2 Pu

I_S(line) = (1/3) × 2 Pu = 0.67 Pu

T_S = (2)² × 0.05 = 0.2 Pu

(d) Star-Delta Starting

I_S = (1/3) × 6 = 2 Pu

T_S = (1/3) × (6)² × 0.05 = 0.6 Pu

(e) Auto transformer starting

T_S = x² × (6)² × 0.05 = 1.0 Pu

X = 0.745 ≈ 75% tap

3. A 50 Hz, induction motor wound for pole-amplitude modulation has 20 initial poles and the modulating junction has 8 poles. At what two speeds will be motor run?

Solution :

P = 20, P_m = 8

P₁ = 20 – 8 = 12

P₂ = 20 + 8 = 28

Hence P₁ poles are suppressed

Speed (20 Poles) = (120 × 50) / 20 = 300 rpm

Speed (28 Poles) = (120 × 50) / 28 = 214.286 rpm

4. Find the percentage tapping required ah an auto transformer required for a squirrel cage motor to start the motor against 1/4 of full load torque. The short- circuit coment on normal voltage is 4 times the full load current and the full load slip of 3%.

Solution :

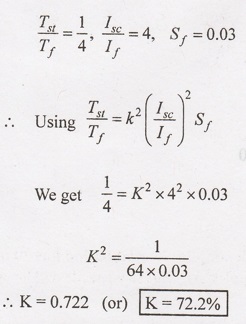
5. A 20 h.p. (14.92 kW), 400V, 950 rpm, 3 φ, 50 Hz, 6 pole cage motor with 480 V applied takes 6 times full load current at stand still and develops 1.8 times full load running torque. The full load current is 30A.

(a) What voltage must be applied to produce full load torque at starting?

(b) What current will this voltage produce?

(c) If the voltage is obtained by an auto-transformer, what will be the line current ?

(d) If starting current is limited to full load current by auto transformer, what will be the starting torque as a percentage of full load torque? Ignore the magnetising???

Solution :

(a) T α V²

T_f α 400²

(b) 6 I_f α 400; I α 298.1

(c) K = 298.1/400

(d) Line current = K² I_SC

Line current = full load current If

30 = K² × 6 × 30 [K² = 1/6]

N_S = (120 ×50)/6 = 1000 rpm

N = 950 rpm

S_f = 50/1000 = 0.05

T_st = 0.37_f (or) 30% F.L. Torque

6. Determine the suitable auto transformation ratio for starting a 3 phase induction motor with line current not exceeding three times the full load current. The shrot circuit current is 5 times the full load current and full load slip is 5%. Estimate also the starting torque in terms of the full load torque.

Solution:

Supply line current = K²I_SC

It is given that supply line current at start equals 3I_f and short circuit current I_SC = 5 I_f where I_f is the full load current

3I_f = K² × 5 I_f (or) K² = 0.6

K = 0.775 (or) 77.5%

In the case of an auto-load startor

T_st = 0.75 I_f = 75% of full load torque.

7. The full load slip of a 400V, 3 phase cage induction motor is 3.5% and with locked rotor, ful! load current is circulated when 92 volt is applied between lines. Find necessary tapping on an auto-transformer to limit the starting current to twice the full-load current of the motor. Determine also the starting torque interms of the full load torque.

Solution :

Short circuit with full normal voltage applied is

I_SC = (480/92) I_f = (100/23) I_f

Supply line current = I_st = 2I_f

Now, line current I_st = K²I_sc

K² = 0.46; K = 0.678 (or) 67.8%

8. The full load efficiency and power factor of a 12 kW, 440V, 3-phase induction motor are 85% and 0.8 lag respectively. The blocked rotor line current is 45 A at 220V. Calculate the ratio of starting to full and current. If the motor is provided with a star-delta staror. Neglect magnetising current.

Solution :

Blocked rotor current will full voltage applied.

I_st / I_f = 52/23.1 = 2.256

9. A 3-phase, 6 pole, 50 Hz Induction motor takes 60A at full load speed of 940 r.p.m. and develops a torque of 150 N.m. The starting current at rated voltage is 300A. What is the starting torque? If a star/delta stator used, determing the starting torque and startor current.

Solution :

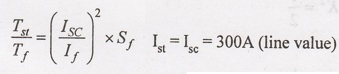
I_f = 60 A (line value)

S_f = (1000-940)/1000 = 0.06

T_f = 150 N-m

λ – Δ Startor used

I_st = (1/3) × I_st with direct starting = 300/3 = 100 A

Starting Torque = 225/3 = 75 N-m

10. Determine approximately the starting torque of an induction motor in terms of full load torque when started by means of (a) a star delta switch (b) an auto transformer with 70.7% tapping. The short circuit current of the motor at normal voltage is 6 times the full load current and the full load slip is 4%. Neglect the magnetising current.

Solution:

= 0.48

T_st = 0.48 T_f (or) 48% of F.L Value

(b) K =0.707 = 1/√2 ; K² = ½

= 0.72

T_st = 0.72 T_f (or) 72% of T_f

11. A 15 h.p. (11.2 kw), 3φ, 6 pole, 5 Hz, 400V, Δ-connected induction motor runs at 960 r.p.m. on full load. If it takes 86.4A on direct starting. Find the ratio of starting torque to full load torque with a star-delta startor. Full load efficiency and power factor are 88% and 0.85 respectively.

Solution:

I_Sc / Phase = (86.4/√3) A

I_st perphase = 1/√3 , I_Sc perphase = 86.4/(√3 × V) = 28.8A

Full load input line current may be found from

√3 × 400 × I_L × 0.85 = 11.2 × 10³ / 0.88

F.L I_ph = 21.59/√3 A

Full-load I_L = 21.59A

I_f = (21.59/√3) A perphase

N_S = 120 × (50/6) = 1000rpm

N = 950; S_f = 0.05

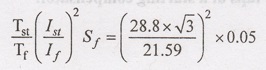
T_st = 0.267 T_f (or) 26.7% F.L Torque

12. Find the ratio of starting current to full load current in a 10 kW (output), 400V, 3-phase induction motor with star/delta startor given that full load p.t. is 0.85, the full load efficiency is 0.88 and ???? at 200V is 40A. Ignore magnetising current.

Solution:

F.L. line current drawn by the D-connected motor may be found from

√3×400×1×0.85=10 × (1000/0.88)

I_L = 19.3A

Now with 200V, the line value of S.C. current of the Δ-connected motor is 40A. If full normal voltage were applied, the line value of S.C. current would be

= 40 × (400/200) = 80A

I_SC (line value) = 80A

I_SC (phase value) = (80/√3)

Since during starting, motor is star connected,

Ist perphase = line value of I_SC = 80/3A

Line value of starting current/live value of F.L current = (80/3)/19.3 = 1.38

13. A5 h.p (3.73 kw), 400V, 3φ, 50Hz cage motor has a full load slip of 4.5%. The motor develops 250% of the rated torque and draws 650% of the rated current when known directly on the line. What would be the line current, motor current and the starting torque if the motor were started (i) by means of a λ-Δ starter and (ii) by converting across 60% taps of a starting compensator.

Solution:

(i) Line current = (1/3) × 650 = 216.7%

λ – connected

I_L = I_ph

Motor current =650/3 = 216.7%

T_st = 250/3 = 83.3%

(ii) Line current = K² × I_SC = (60/100)² × 650 = 234%

Motor current = K × I_SC = (60/100) × 650 = 390%

T_st = K² × T_SC = (60/100)² × 250 = 90%

14. An 6 pole, 3 phase induction motor is connected to 50 Hz supply. If it is running at 960 rpm, find the slip.

Solution:

Given data:

(i) P = 6, (ii) f= 50 Hz, (iii) N = 960 rpm.

Synchronous Speed,

N_S = 120 ƒ / P = (120×50)/6

N_S = 1000 rpm.

S = 0.04 (or) 4%.

15. An 2 pole, 3 phase, 50 Hz induction motor is running on no load with slip of 4% calculate.

(i) Synchronous Speed (ii) Speed of the Motor.

Solution:

Given data:

1. P=2, 2. f= 50 Hz, 3. S=4% (or) 0.04.

(i) Synchronous Speed (N):

N_S = 120 f / P = (120×50) / 6

N_S = 3000 rpm.

(ii) Speed of the Motor (N):

N = N_S (1-S) = 3000 (1 − 0.04)

N = 2880 rpm.

16. An 3 φ, 4 pole, 50 Hz induction motor is running at 1440 rpm determine the slip speed and slip.

Solution:

Given data:

1. No. of poles, P = 4, 2. Supply frequency, f= 50 Hz, 3. Motor speed, N = 1440 rpm.

To find:

(i) Slip speed.

(ii) Slip.

Solution:

(i) Slip Speed (N_S - N):

N_S = 120 f / P = (120×50)/4 = 1500 rpm

N_S - N = 1500 - 1400 = 60

Slip Speed = 60 rpm.

(ii) Slip (S):

S = (N_S - N)/N_S = (1500-1400)/1500

S = 0.04.

17. A 6 pole, 50 Hz, 3 φ induction motor runs at 800 rpm at full load. Determines the value of slip at this load condition.

Solution:

Given data:

1. No. of poles, P = 6, 2. Frequency, f= 50 Hz, 3. Speed, N = 800 rpm.

To find:

(i) Slip (S):

S = ((N_S-N)/N_S) × 100

N_S = 120ƒ/P = (120×50)/6 = 1000rpm

S = ((1000-800)/1000) × 100

S = 0.2 (or) 20%.

18. An 3-phase, 50 Hz induction motor run at 960 rpm on full load, find the number of poles and slip speed.

Solution:

Given data:

(i) Frequency, F = 50 Hz, (ii) Speed, N = 960 rpm.

To find:

(i) No. of poles P.

(ii) Slip speed (N_S−N).

1000 rpm is the nearest synchronous speed for 960 rpm.

N_S = 120ƒ/P ═> P = 120f/Ns = (120×50)/1000 = 6

P= 6.

Slip speed = N_S - N = 1000-960 = 40 rpm.

Slip Speed = 40 rpm.

19. An 3 phase, 6 pole, 50 Hz induction motor runs at 960 rpm. Find the slip.

Solution:

Given data:

(1) No. of poles, P = 6. (2) Frequency, F = 50 Hz. (3) Motor speed, N = 950 rpm.

To find:

(1) Slip (S).

Synchronous Speed

N_S = 120ƒ/P = (120×50)/6

N_S = 1000 rpm.

Slip:

S = ((N_S - N)/N_S) × 100 = ((1000-950)/1000) × 1000 = 0.05 (or) 5%

S = 5%.

20. The following data refers to a 10-pole, 400 V, 50 Hz 3φ induction motor R₁=1.75 Ω, X₁ = =5.5 Ω, R₂^' = 2.25 Ω, X₂^' = 6.6 Ω. When the motor is tested on no- load, it is observed that it takes 3.8 A (line current) and the total core loss is 310 W. By using approximate equivalent circuit at 4% slip, calculate: (i) The rotor current, (ii) Supply current and power factor, (iii) Mechanical power developed, (iv) Gross load torque and (v) Draw the equivalent circuit.

Solution:

Stator resistance R₁ = 1.75 Ω

Stator reactance X₁ = 5.5 Ω

Rotor resistance referred to stator R₂' = 2.25 Ω

Rotor reactance referred to stator X₂' = 6.6 Ω

Total core loss = 310 W

No-load line current I_0­ = 3.8 A

If cos φ₀ is the power factor at no-load, then

√3 V_L I₀ cos φ₀ = 310

 

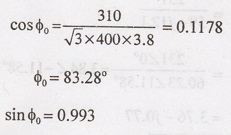
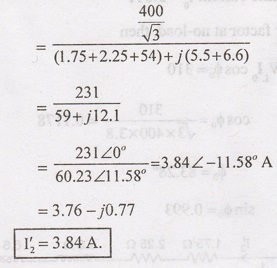
21. A 220 V, 3 phase, 4 pole, 50 Hz Y-connected induction motor is rated 3.78 kW the equivalent circuit parameter are R1 = 0.45 Ω, X1 = 0.8 Ω, R2' = 0.4 Ω, X2' = 0.8 Ω, B0=1/30. The stator core loss is 50 W and rotational losses is 150 W. For a slip of 0.04, find input current, Pf, air gap power, mechanical power, electromagnetic torque output power and efficiency. Draw the equivalent circuit and mark the parameters given.

Solution:

(i) Power factor = cos 25.8 = 0.9 lag

cos φ = 0.9 lagging.

(iii) Mechanical power developed P_m

P_m = (1-S) P₂ = (1 - 0.04) x 4.52 = 3986 W

P_m = 3986 W.

22. A 4 pole alternator has an armature with 85 slots and 8 conductors per slot and rotates at 1500 rpm and the flux per pole is 0.05 wb. Calculate the emf generated, if winding factor is 0.96 and all the conductors are in series.

Solution:

N = 1500 rpm, φ = 0.05 wb, f=50 Hz, P = 4,

No.of Slots = 25, No. of Conductor/Slot = 8.

No. of armature conductors = 25 × 8 = 200

No. of turns T_ph = Z_ph/2 = 200/2 = 100

Winding factor k_w = k_p k_d = 0.96

f = PN/120 = (4×1500)/120 = 50 Hz.

Generated emf/phase = 4.44 f φ T_ph k_d k_p = 4.44 × 50 × 0.05 × 100 × 0.96 Volts

E_ph = 1065.6 Volts.

23. A 4 poles 50 Hz star connected alternator has a flux per pole of 0.12 wb. It has 4 slots per pole of phase, conductors per slot being 4. If the winding coil span is 150°, find the emf.

Solution:

No. of slots/pole/phase m = 4.

No. of slots per pole n = m × No. of phases = 4 × 3 = 12.

No. of slots per phase = m × No. of poles = 4 × 4 = 16.

No. of conductors connected in series per phase.

Z_ph = No. of conductors/slot × No. of slots per phase = 4 × 16 = 62.

No. of turns per phase, T_ph = Z_ph/2 = 64/2 = 32.

Angular displacement between the slots, B = 180°/n = 180°/12 = 15.

k_d = sin 30°/4 sin 7.5° = 0.5/0.5221 = 0.9576

Chording angle α = 180° - Coil span = 180° - 150° = 30°

Pitch factor k_p = cos α/2 = cos (30°/2) = 0.9659

Phase voltage = 4.44 f φ T_ph k_d k_p = 4.44 × 50 × 0.12 × 32 × 0.9686 × 0.9576

E_ph = 788.497 V

Line voltage = E_L = √3 × 788.497 = 1365.718 Volts

E_L = 1365.718 V

24. A three-phase induction motor is supplied at 50 Hz and is wound for 4 poles. Calculate (i) Synchronous speed, (ii) Speed when the slip is 3%, (iii) Frequency of the rotor emf when it runs at 1200 rpm.

Solution:

Supply frequency f= 50 Hz, No. of poles P = 4.

(i) Synchronous Speed N_S = 120ƒ/P = (120×50)/4 = 1500 rpm

N_S = 1500 rpm.

(ii) Speed when the slip 8%

S = 0.03

N = N_S (1-S) = 1500 (1-0.03)

N=1455 rpm.

(iii) N=1200 rpm

f_f = S_f,

Slip (S) = (N_S - N)/N_S = (1500-1200)/1500 = 0.2

f_r = 0.2 × 50

f_r = 10 Hz.

25. For a 4 pole, 3φ, 50Hz induction motor ratio of stator to rotor turns is 3. On a certain load, its speed is observed is to be 1450 rpm. When connected to 415 V supply calculate (i) frequency of rotor emf in running condition, (ii) magnitude of induced emf in the rotor at standstill, (iii) magnitude of induced emf in the rotor under running condition. Assume star connected stator.

Solution:

P = 4, f= 50 Hz, E_IL = 415 V Stator Side line voltage = 415 V Stator Side line voltage

k = Rotor turns / Stator turns = 1/8 = 0.333; N = 1450 rpm.

(i) N_S = 120ƒ/P = (120×50)/4 =1500 rpm

N = 1450 rpm

S = (N_S - N)/N_S = (1500–1450)/1500 = 0.033

f_r = S_f = 0.033 × 50 = 1.66 Hz.

(ii) Magnitude of induced emf in the rotor at standstill (E_2ph)

k = E_2ph / E_lph = rotor turns / stator turns

E_1ph = Stator side phase voltage

E_1L =415 V; E_2ph = rotor side phase voltage

E_1ph = 415/√3 = 239.6 V ; E_2ph/E_1ph = 0.333

E_2ph = 0.333 × 239.6 V

E2ph = 79.78 V.

(iii) Under Running condition

E_2r = SE₂ = 0.033 × 79.78 = 2.68 V.