Properties of Fourier Series

PROPERTIES OF FOURIER SERIES

The properties of the Fourier series are as follows.

(i) Linearity

(ii) Time shift

(iii) Frequency shift

(iv) Scaling

(v) Differentiation in time

(iv) Convolution in time

(vii) Modulation

(viii) Symmetry

(i) Linearity

The Fourier series equation is given by

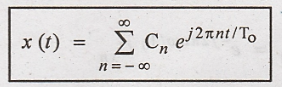
From the above equation, x(t) has the Coefficient C_n. Let these coefficient be defined as C_{x n}.

The signal x(t) & its coefficients C_{x n} is called the Fourier series Pair.

Now let us consider Two signals x₁(t) & x₂(t) which are defined as follows.

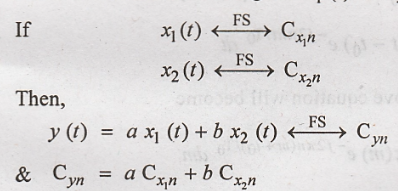
To Prove:

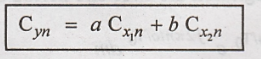
Proof:

By definition of C_x, the equation is given as,

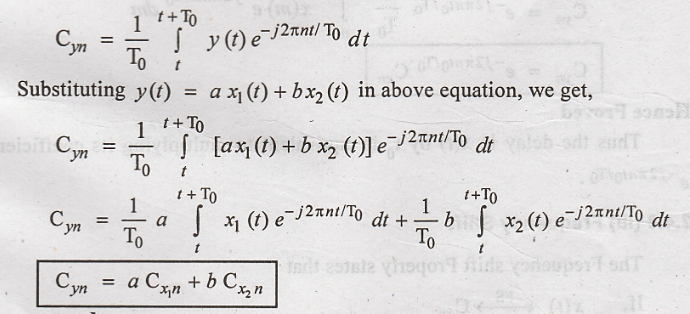
Hence proved

Thus from the above equation the Fourier series coefficients are also linearly related.

(ii) Time Shift

It states that

To Prove:

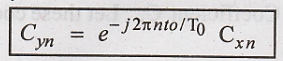
Proof :

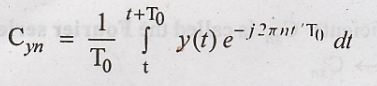
Substituting y(t) = x(t-t₀) in the above equation,

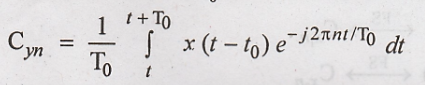
Let t - t₀ = m, then the above equation will become

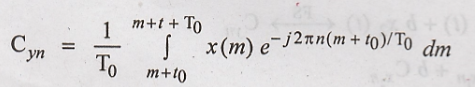
In the above equation the limits of integration are over one period of x(m)

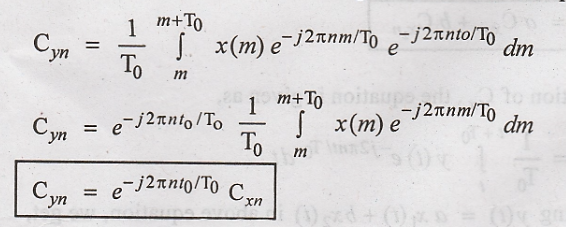
Hence Proved

Thus the delay in x(t) by t0 is equivalent to multiplying its coefficient by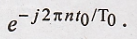 

(iii) Frequency Shift

The Frequency shift Property states that

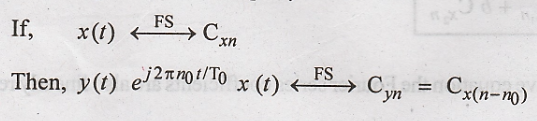
To Prove:

Proof :

By definition of C_n, we have,

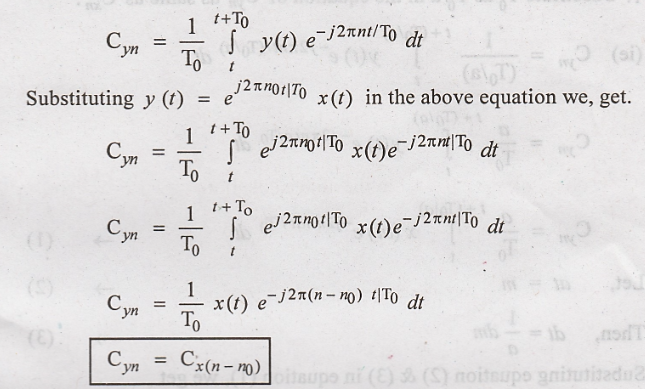
Hence Proved

Thus shifting the frequency components by n_o is equivalent to multiplying x(t) by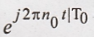 

(iv) Scaling

The scaling property stats that,

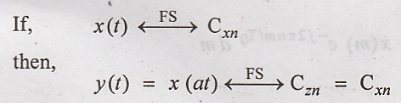
To Prove:

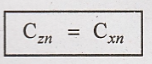
Proof:

By definition of C_n, we have,

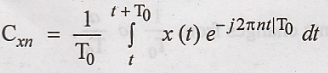
If x(t) is periodic then y(t) = x(at) is also Periodic

If T is the period x(t), then period of y(t) will be T/a.

.'. Substitute T₀ as T₀/a in the equation of C_yn as same as C_xn.

Substituting equation (2) & (3) in equation (1), we get

Hence Proved

Thus after Time scaling, the Fourier series Coefficients are same. But the spacing between the components changes from 1/T₀ to a/T₀.

(v) Differentiation in Time

This property states that,

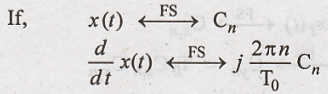
To Prove:

Proof :

From the definition of Fourier series x(t) can be written as,

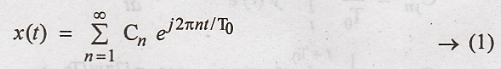
Differentiating both sides with respect to 't',

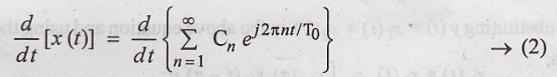
Changing the order of summation & Differentiation,

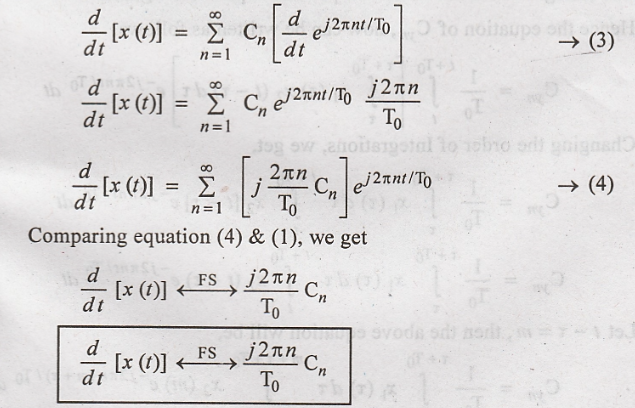
Hence Proved

Thus differentiating the signal is equivalent to multiplying its coefficients by j2πn/T₀.

(vi) Convolution in Time

This property states that,

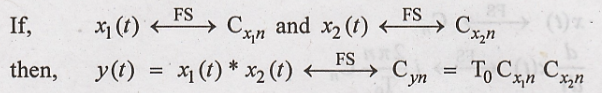
To Prove:

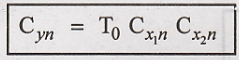
Proof :

By the Fourier series definition, we have the equation as,

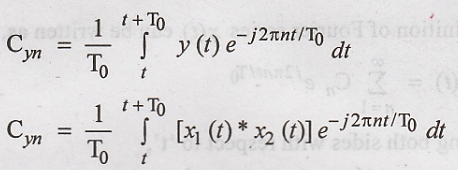
Substituting y(t) = x₁(t) * x₂(t) in the above equation and using the convolution formula,

The intergration is above for one period for periodic signals.

Hence the equation of C_yn, now can be written as follows,

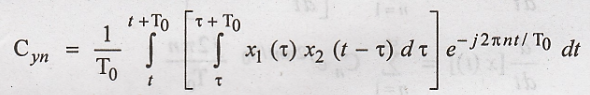
Changing the order of Integrations, we get,

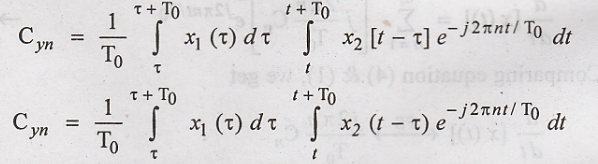
Let t - τ = m, then the above equation will be,

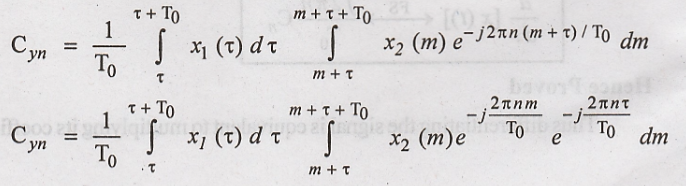
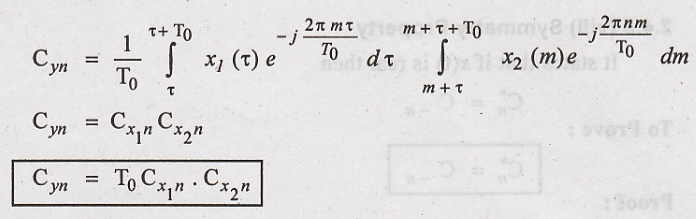
Hence Proved.

Thus the Convolution of the two sequences results in multiplication of their coefficients and T₀.

(vii) Modulation

This property states that,

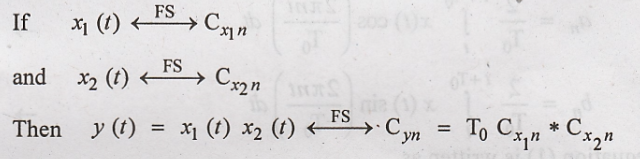
To Prove:

Proof :

The term inside the bracket indicates Fourier co-efficient X₂(n-m)

(viii) Symmetry Property

It states that if x(t) is real then

To Prove:

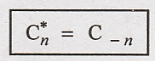
Proof :

Quadrature/Trignometric Fourier series :

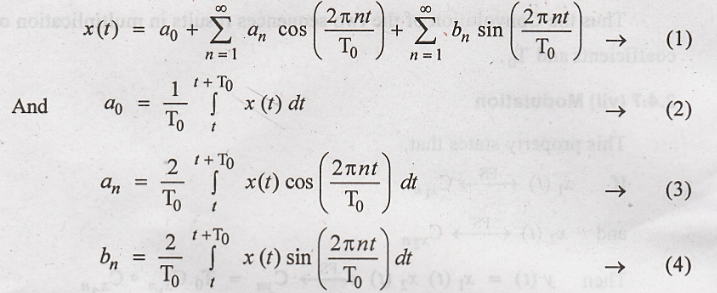
The equation (1) is written as,

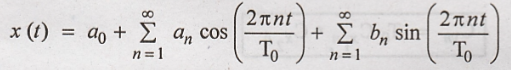
Let us use Euler's identity in the above equation (i.e).,

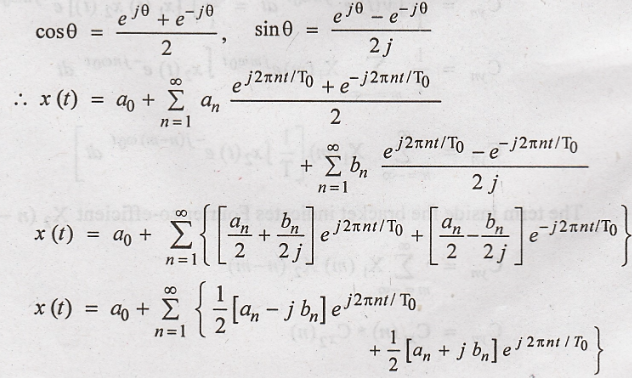
Then, complex conjugate of C_n will be,

Substituting the values of a_n & b_n from equation (3) & (4) in equation (5) & (6)

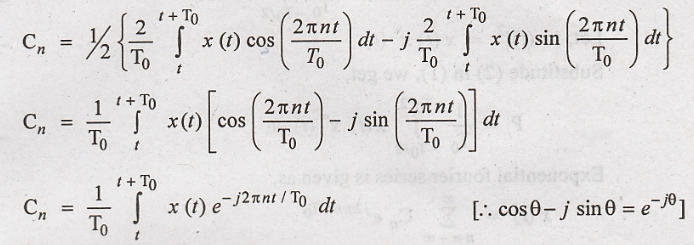
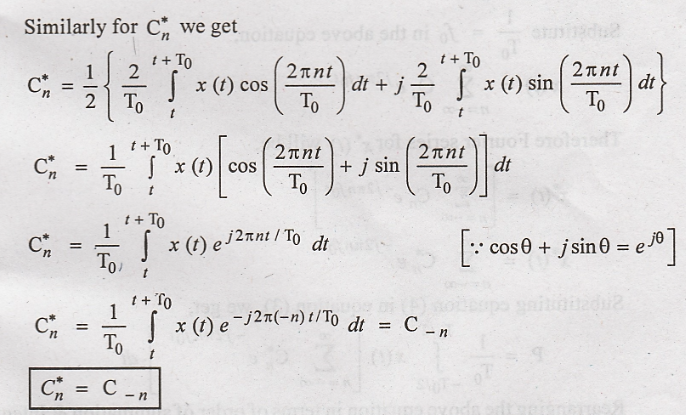
Hence Proved.

Parseval's Power Theorem

Statement of the Theorem:

It states that the Total average power of the periodic signal x(t), is equal to the sum of the average powers of its phasor components.

Parseval's Power Theorem:

Total Average Power: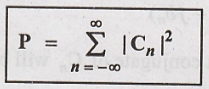 

Proof :

The Total Normalized average power 'P' of the signal x (t) is given as,

Substitute (2) in (1), we get,

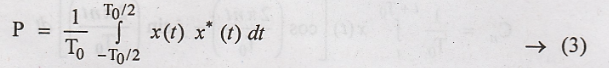
Exponential fourier series is given as,

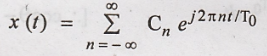
Substitute 1/T₀ = f₀ in the above equation,

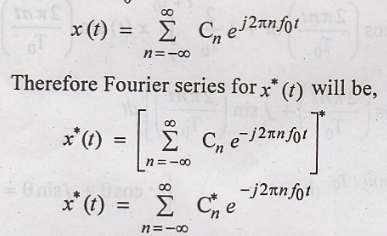
Therefore Fourier series for x*(t) will be,

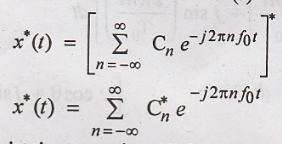
Substituting equation (4) in equation (3), we get,

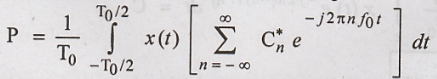
Rearranging the above equation in terms of order of summation & Integration.

Hence Parseval's Theorem is proved