Signals and Systems: Unit II: Analysis of Continuous Time Signals,,
Problems Based on Fourier Transform
Inverse Fourier Transform
Problems based on fourier transform and Inverse fourier transform
Problems Based on Fourier Transform
1. Obtain the Fourier
transform of unit step signal u(t).
Solution:
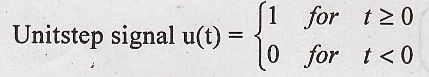
Fourier transform of
x(t)

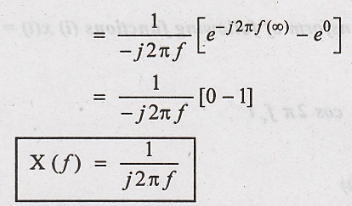
2. Obtain the Fourier
transform of unit impulse function δ(t)
Solution:

Fourier transform of
x(t)
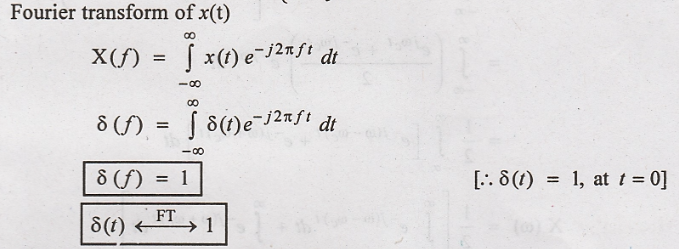
3. Obtain the Fourier
transform of x(t) = 1
Solution:
Fourier transform of
x(t)

4. Obtain the Fourier
transform of following functions (i) x(t) = cos ωct (ii) x(t) = sin
ωct
(i)
x(t) = cos ωct (or) cos 2π fct
Solution:
Fourier transform of
x(t)

(ii)
x(t) = sin ωct
Solution
:
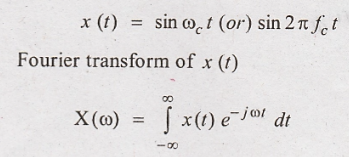

5. Obtain the Fourier
transform of following signals (i) x (t) = cos ω0t (ii) x(t) = sin ω0t
(i)
x(t) = cos ω0t
Solution:
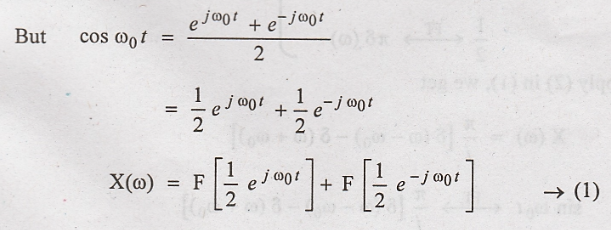
From frequency shifting
property
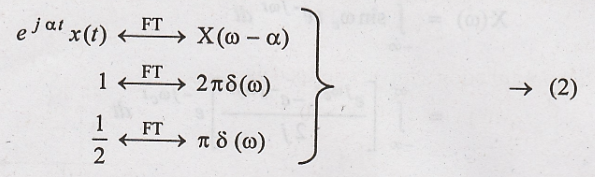
Apply (2) in (1), we
get
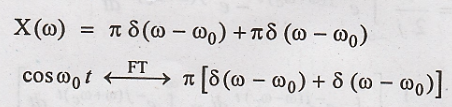
(ii)
x(t) = sin ω0t
Solution:
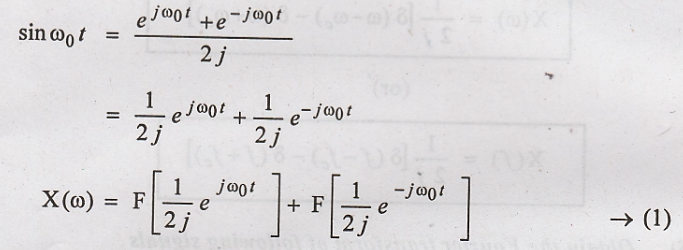
From frequency shifting
property
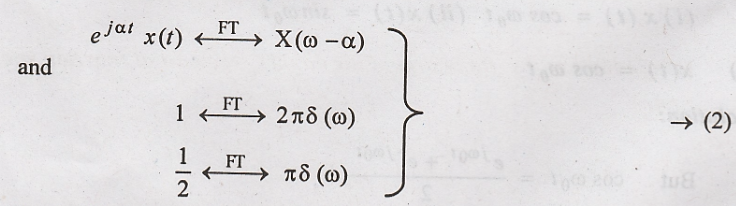
Apply (2) in (i), we
get
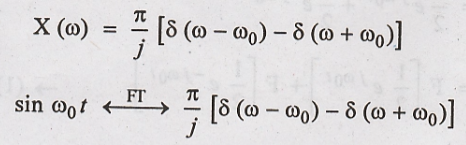
6. Obtain the Fourier
transform of x(t) = sgn(t)
Solution:
Signum function sgn(t)
is defined as
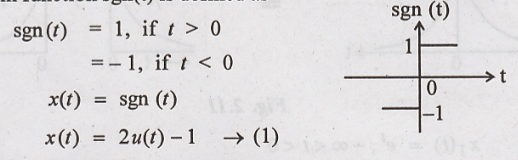
Differentiate on both
sides of (1).
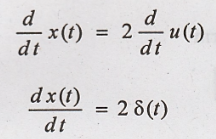
By taking Fourier
transform on both sides
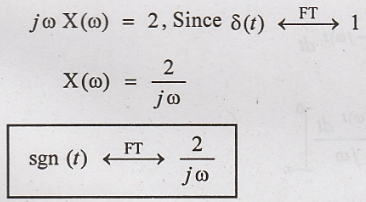
7. Obtain the Fourier transform
of the double exponential function shown in
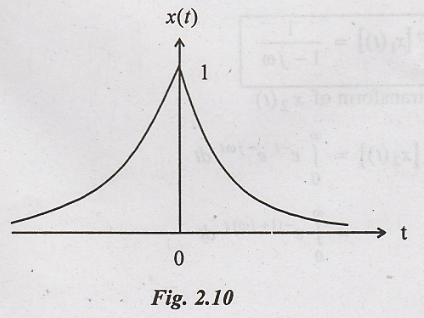
Solution
:
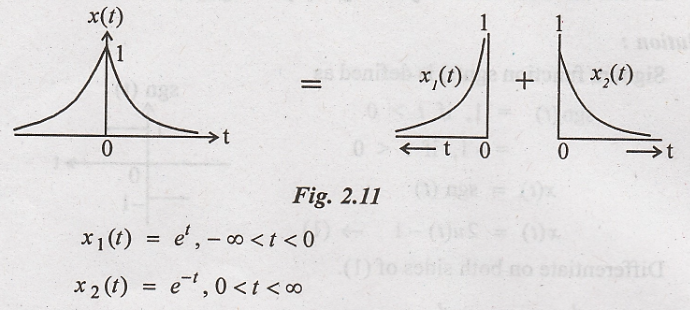
By linearity property
of Fourier transform

Fourier transform of x2(t)
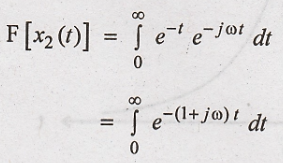
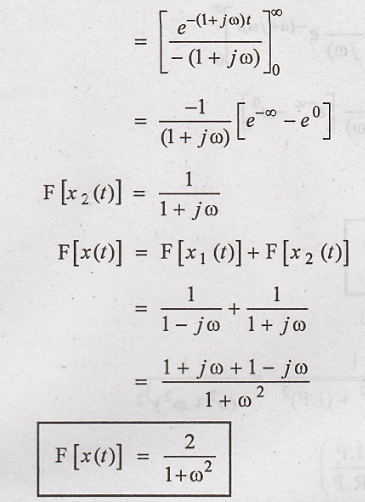
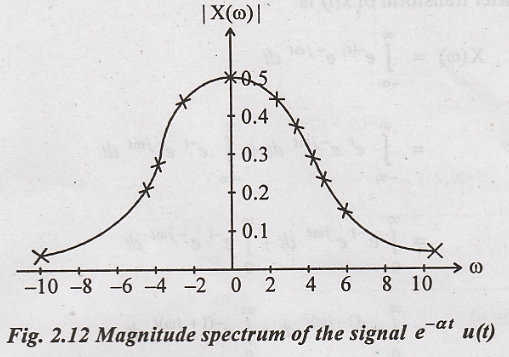
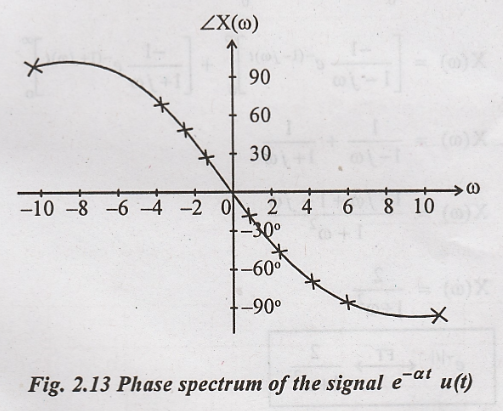
8. Find the Fourier
transform of the signal x(t) = e – a t u(t) and sketch the magnitude
and phase spectrum.
Solution:
x(t) = e – a t
u(t)
Fourier transform of
x(t)
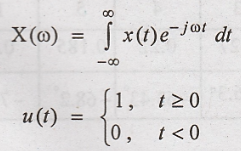
So, limits of
integration changes from 0 to ∞
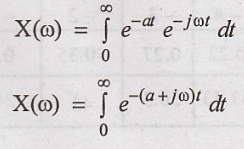
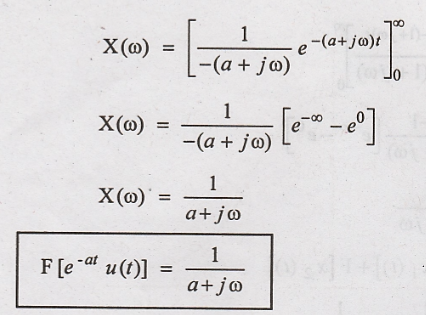
Magnitude
of
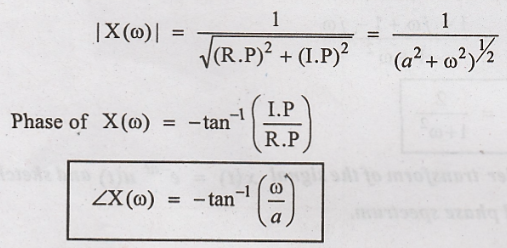
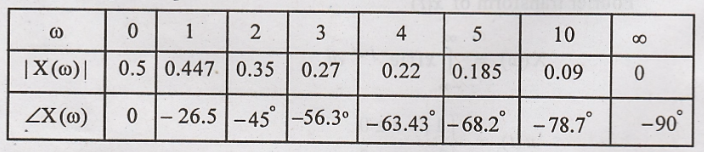
|X(ω)| and < X(ω) are
tabulated for various values of @ to sketch the magnitude and phase spectrum.
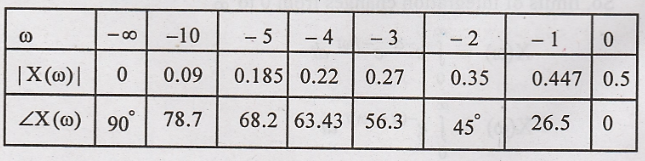
For negative Values of
ω
9. Find the Fourier
transform of x(t) = e - |t|
Solution:
x(t) can be expressed
as
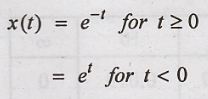
Fourier transform of
x(t) is
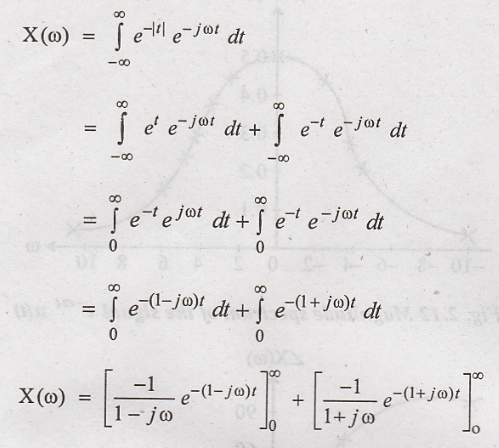
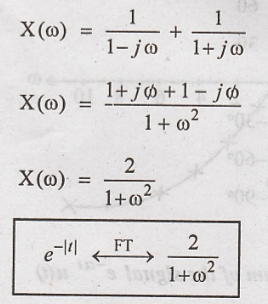
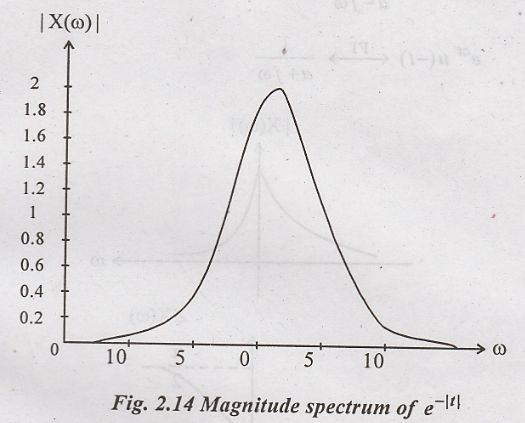
Magnitude
of X(ω)
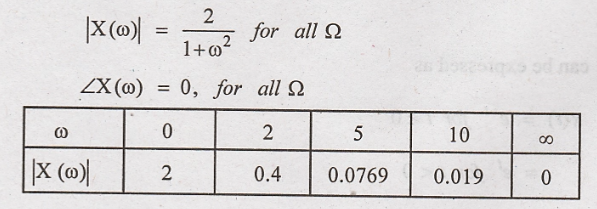
For positive values of
ω

10. Obtain the Fourier
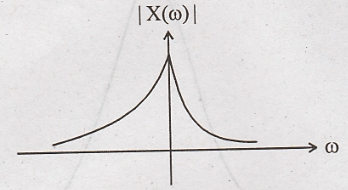
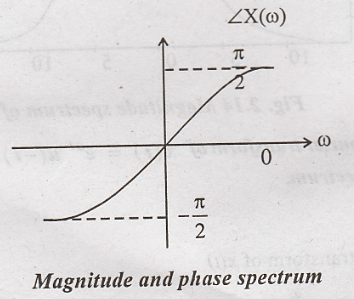
transform of x(t) = eat u(-t) and plot the magnitude and phase
spectrum.
Solution:
Fourier transform of
x(t)
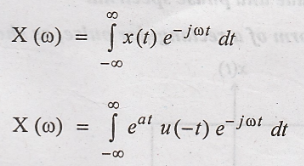
But u(-t) = 1, for 0 to
-∞, So integration limits change from 0 to -∞.
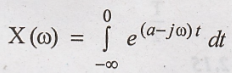
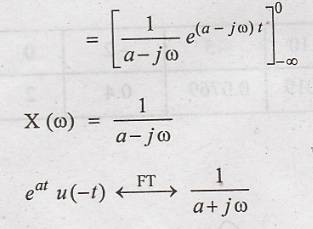
11.
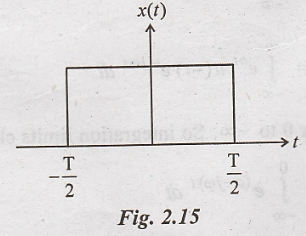
Obtain the Fourier transform of a rectangular pulse, as shown in Fig.
Solution
:
Rectangular pulse is defined
as
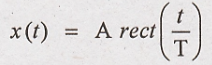
Fourier transform of
x(t) is
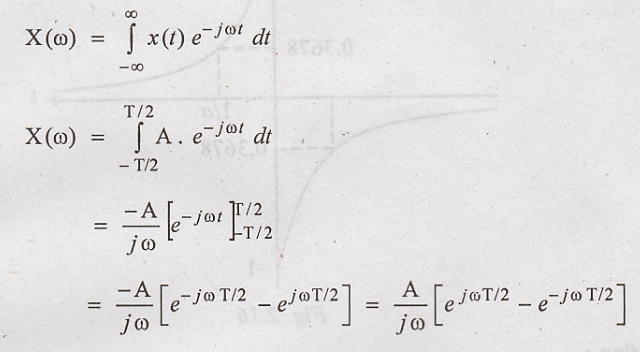

12. Obtain the Fourier
transform of the antisymmetric exponential pulse as shown in figure.
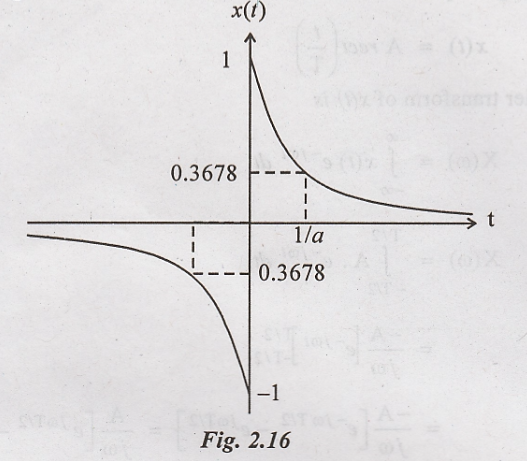
Solution:
x(t) can be represented
as
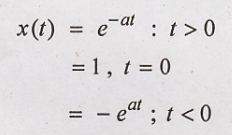
Fourier transform of
x(t)
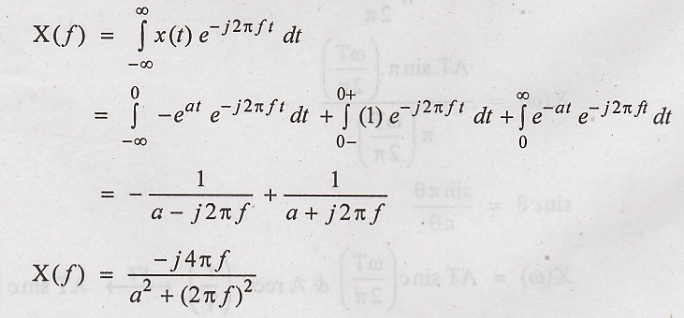
13. Obtain the Fourier
transform of x(t) = e j 2 π fc t
Solution:
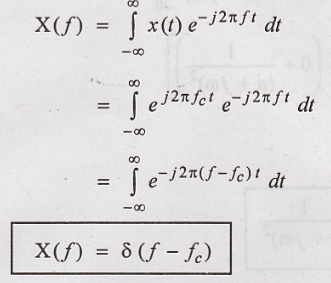
14. Obtain the Fourier
transform of x(t) = t e – a t u(t)
Solution:
Fourier transform of
x(t) is
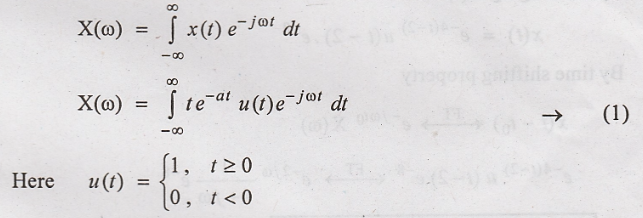
So limits of
integration of (1) changes into 0 to ∞.
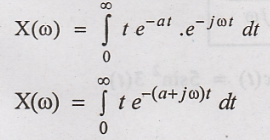
Integrating by parts
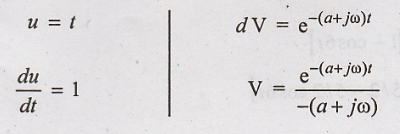
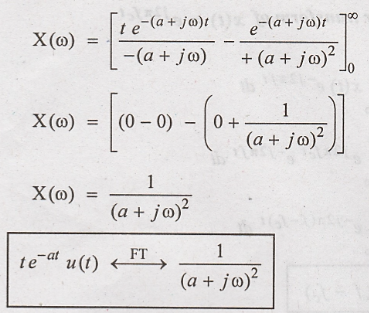
15. Find the Fourier
transform of x(t) = e – 4 t u(t-2)
Solution:
By rearranging x(t)
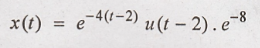
By time shifting
property
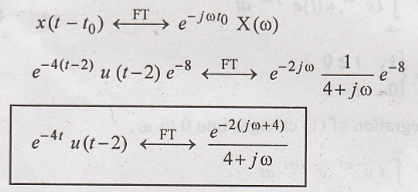
16. Find the Fourier
transform of x(t) = 5 sin23(t)
Solution
:
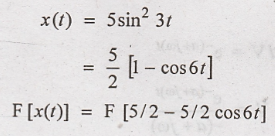
By using linearity
property
Inverse Fourier Transform
Steps to find inverse
Fourier transform of X(ω)
Step 1:
Convert X(ω) by using
partial fraction expansion in the form of
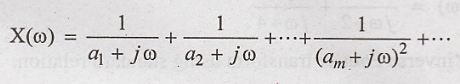
Step 2:
Then obtain inverse
Fourier transform using standard Fourier transform pairs. Problems based on
inverse Fourier transform:
1. Obtain inverse
Fourier transform of the following signal.
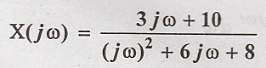
Solution:
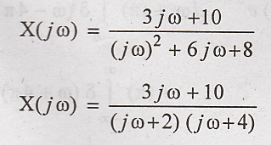
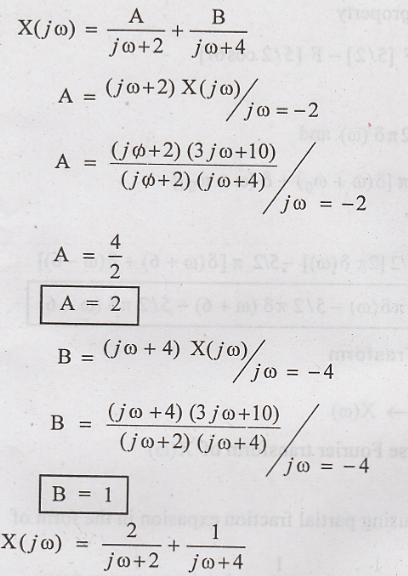
By taking the inverse
Fourier transform using standard relation.
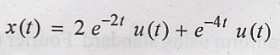
2. Obtain the inverse
F.T of 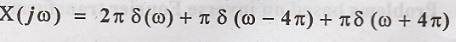
Solution
:
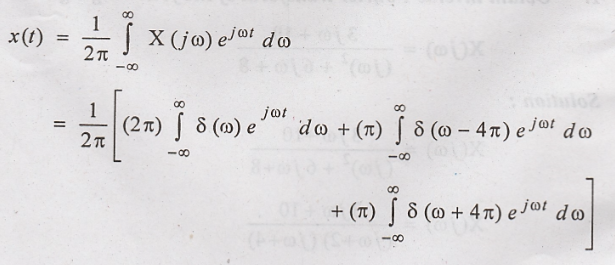
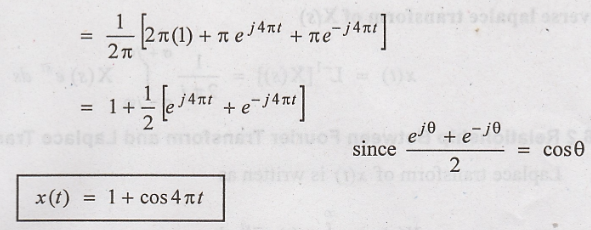
Signals and Systems: Unit II: Analysis of Continuous Time Signals,, : Tag: : Inverse Fourier Transform - Problems Based on Fourier Transform
Related Topics
Related Subjects
Signals and Systems
EC3354 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
