Signals and Systems: Unit II: Analysis of Continuous Time Signals,,
Laplace Transform
Laplace transform pair, Relationship Between Fourier Transform and Laplace Transform
Continuous time systems are analyzed using Lapalce transform. Unstable system is also analyzed using Lapalce transform.
LAPLACE
TRANSFORM
Continuous time systems
are analyzed using Lapalce transform. Unstable system is also analyzed using
Lapalce transform.
Types of Lapalce
transform
There are 2 types of
Laplace transform
(1) Unilateral (or) one
sided Laplace transform
(2) Bilateral (or) two
sided Laplace transform
Definition of Laplace Transform
Laplace transform of
signal x(t) is defined as
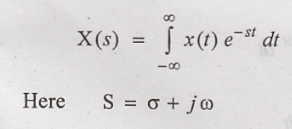
σ ⇒ Real part of S &
it is denoted as attenuation constant
ω ⇒ Imaginary part of
"S" and it is denoted as angular frequency.
Laplace transform pair
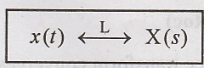
x(t) is obtained from
X(s) by taking inverse Laplace transform of X(s)
Inverse lapalce transform of X(s)
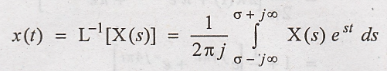
Relationship Between Fourier Transform and Laplace Transform
Laplace transform of x(t) is written as
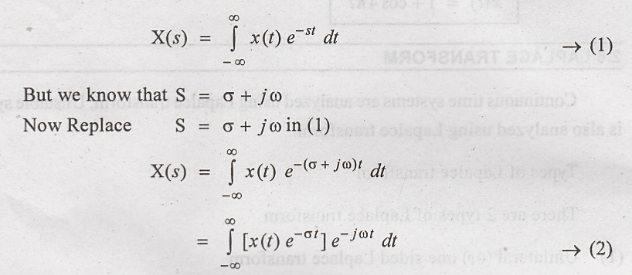
(2) is Fourier
transform of x(t) e – σ t
Hence Laplace transform
is Fourier transform of x(t) e – σ t
If σ = 0, then S = j ω
Now Laplace transform
of x(t) is given as
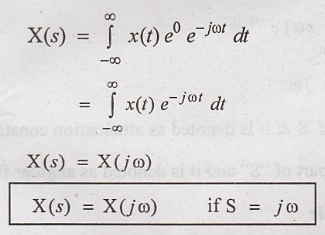
Region of convergence of Laplace transform (Roc)
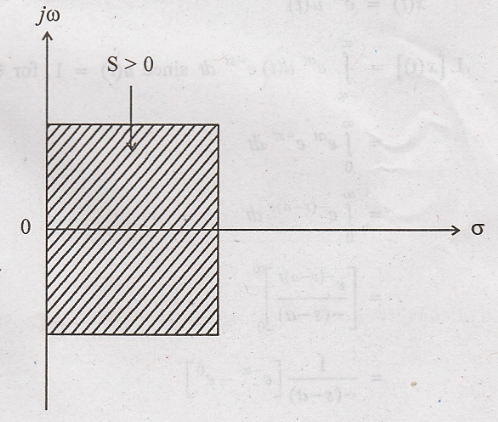
The range of values of
"σ" for which Laplace transform converges is known as Region of
convergence.
Problems Based on Laplace Transform
1. Find Laplace
transforms and Roc of x(t) = u(t)
Solution
:

2. Find Laplace
transform of δ(t)
Solution
:
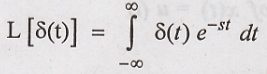
Shifting property of
δ(t)
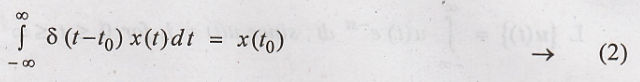
Compare (1) & (2)
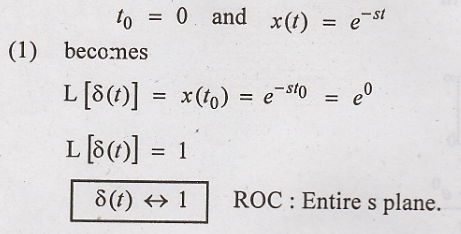
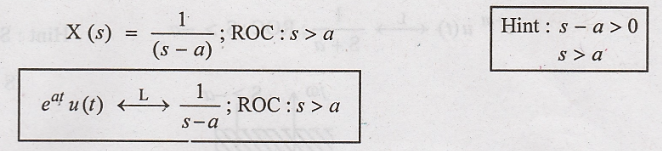
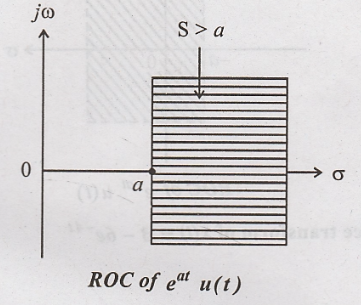
3. Find Laplace
transform of x(t) = e a t u(t) and plot its ROC.
Solution
:
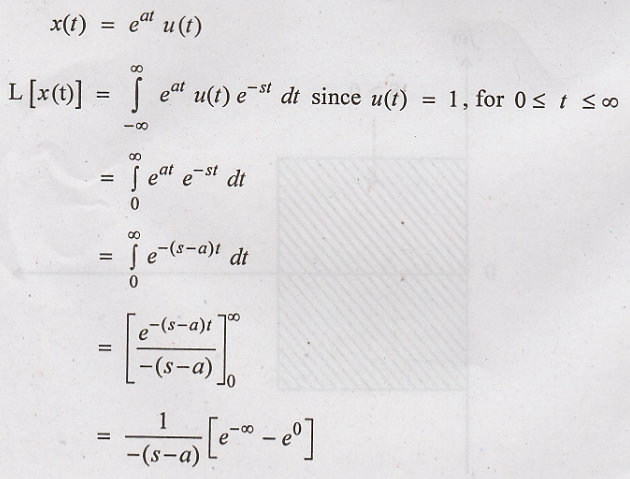
4. Find Laplace
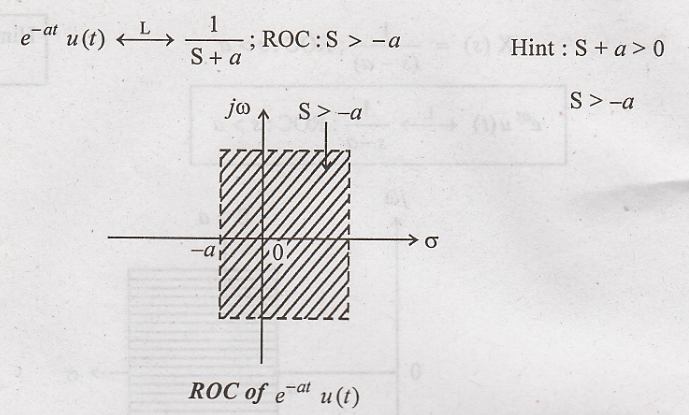
transform of x(t) = e – a t u(t)
Solution
:
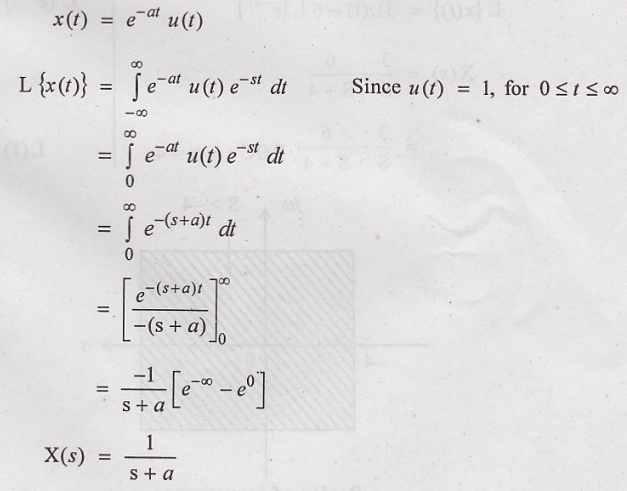
5. Find Laplace
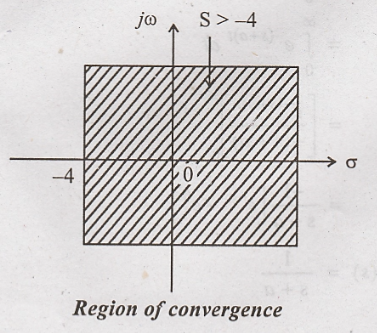
transform of x(t) = 3 - 6e – 4 t
Solution
:
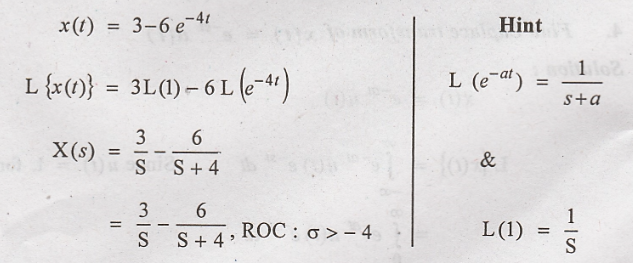
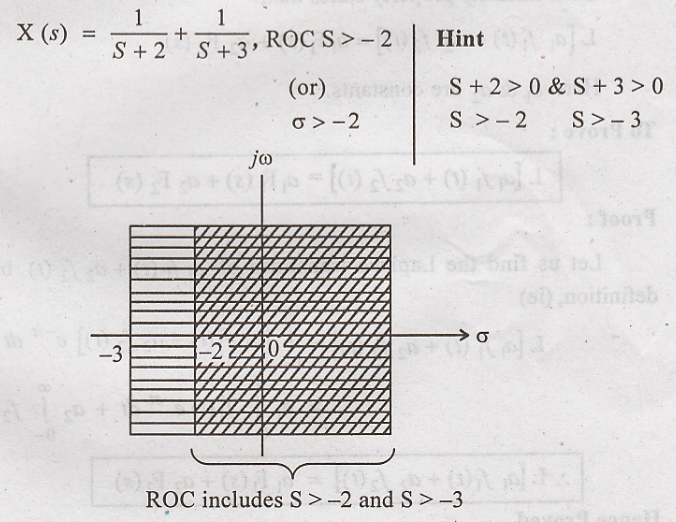
6. Determine Laplace
transform of x(t) = e – 2 t u(t) + e – 3 t u(t) and
sketch its ROC
Solution
:
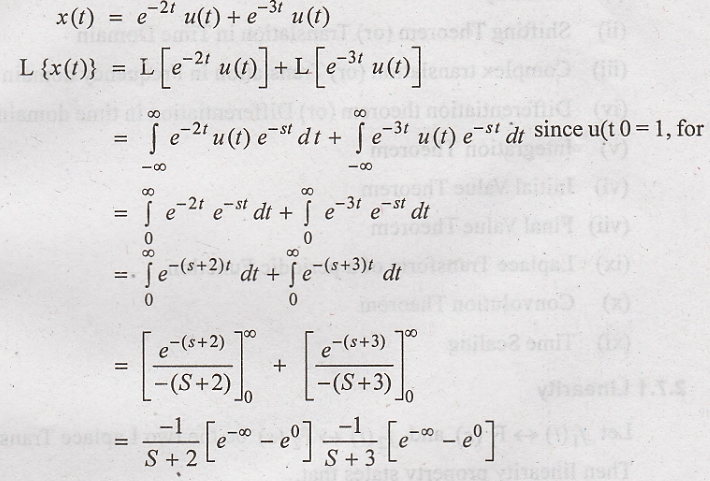
Signals and Systems: Unit II: Analysis of Continuous Time Signals,, : Tag: : Laplace transform pair, Relationship Between Fourier Transform and Laplace Transform - Laplace Transform
Related Topics
Related Subjects
Signals and Systems
EC3354 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
