Inverse Laplace Transform

INVERSE LAPLACE TRANSFORM

Inverse Laplace transform of any function F(S) is obtained by the following methods

a. Inverse Laplace transform using partial fraction expansion

b. Inverse Laplace transform using convolution integral.

Inverse Laplace Transform using Partial Fraction Expansion

Case 1: Simple and real roots.

X(s) is expanded in partial fraction as

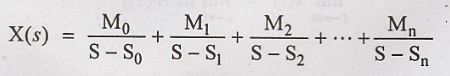
Here the roots S₀, S₁, S₂ are considered as real.

Then value of M₀, M₁, M₂, ... M_n are calculated as follows.

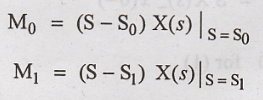
Then general equation is written as.

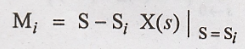
(1) Determine inverse Laplace transform of following function.

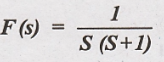
Solution:

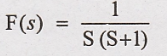
By using partial fraction expansion, F(s)can be written as

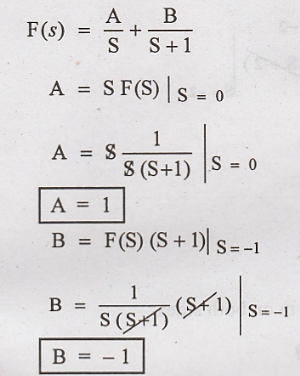
Substitute A & B value in F(s)

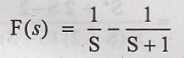
Taking inverse Laplace transform on both sides.

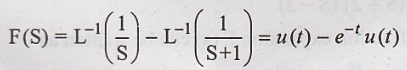
(2) Find inverse Laplace transform of X(s) =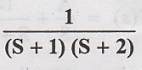 

Solution:

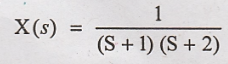
By using partial fraction expansion X(s) can be written as

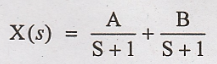
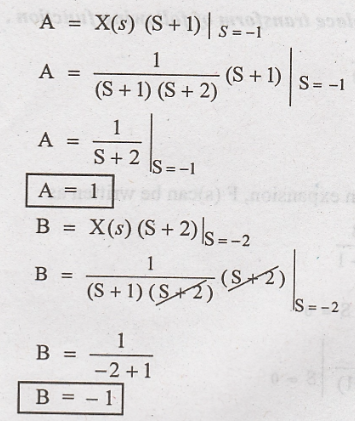
Substitute A & B value in X(s)

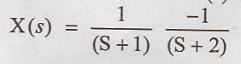
Taking inverse Laplace transform on both sides

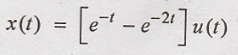
3. Find inverse Laplace transform on F(s) =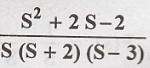 

Solution:

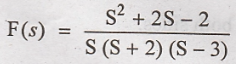
By using partial fraction expansion F (s) can be written as

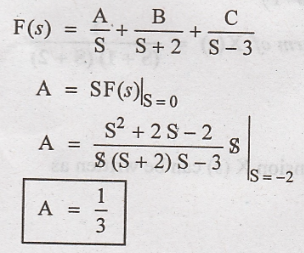
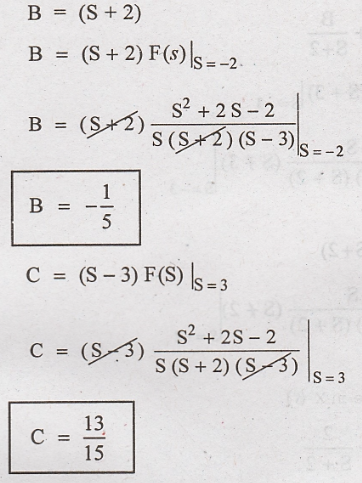
Substitute A,B,C Values in F (s)

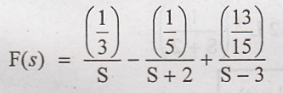
Taking inverse Laplace transform on both sides

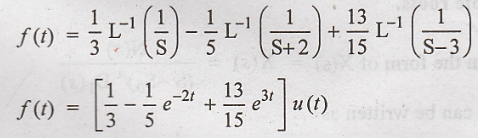
4. Obtain the inverse Laplace transform of the following function

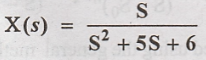
Solution:

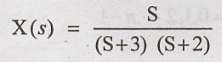
Substitute A & B value in X(s)

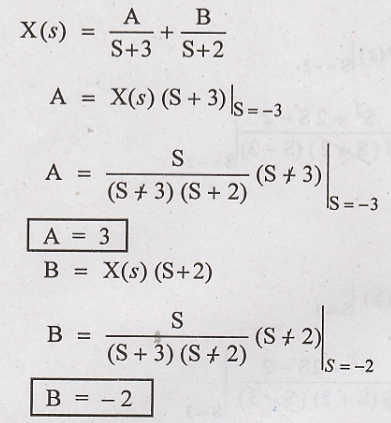
Taking inverse Laplace transform on both sides

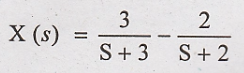
Case ii: Multiple roots.

If X(s) is in the form of X(s) =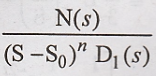 

Then F (s) can be written as

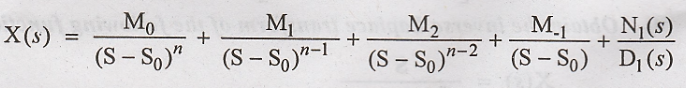
M₀, M₁, M₂, ... M_n-1 values are calculated using the general method as follows,

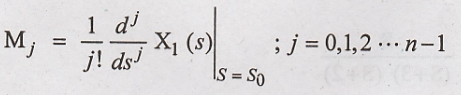
1. Find the inverse Laplace transform of the following function.

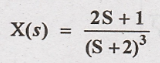
Solution:

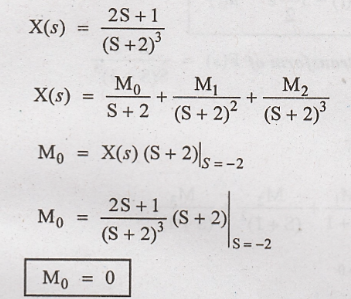
First we should calculate M₂. Then M₁ is calculated.

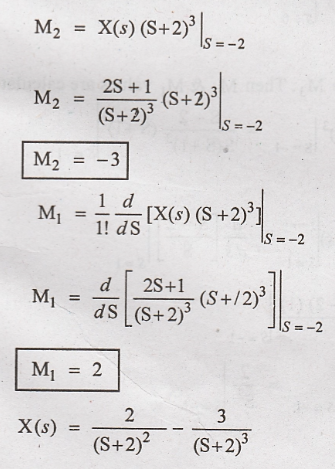
Taking inverse Laplace transform on both sides.

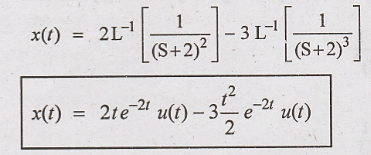
2. Find inverse Laplace transform of F(s) =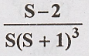 

Solution:

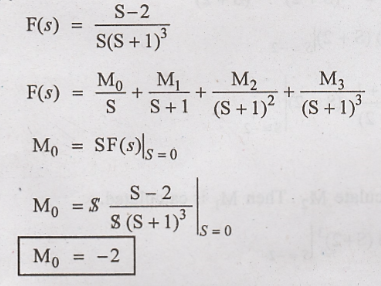
First we should calculate M₃. Then M₂ & M₁ values are calculated.

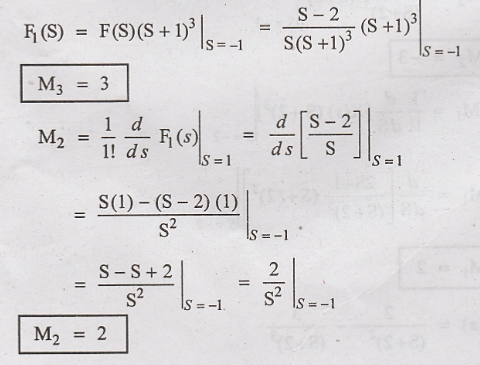
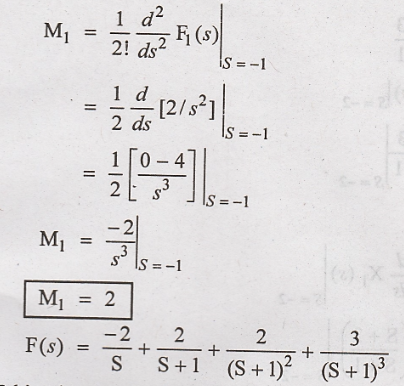
Taking inverse Laplace transform on both sides

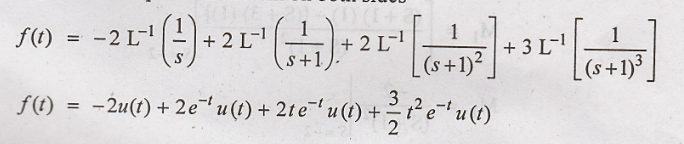
3. Find the inverse laplace transform of X(s) =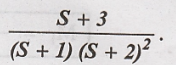 

Solution:

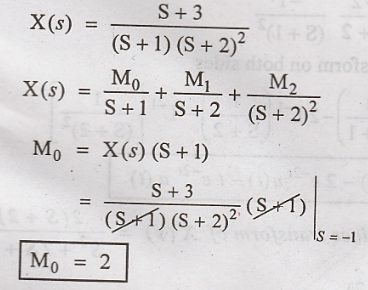
First we should calculate M₂. Then M₁ is calculated.

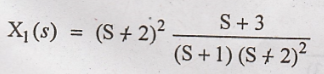
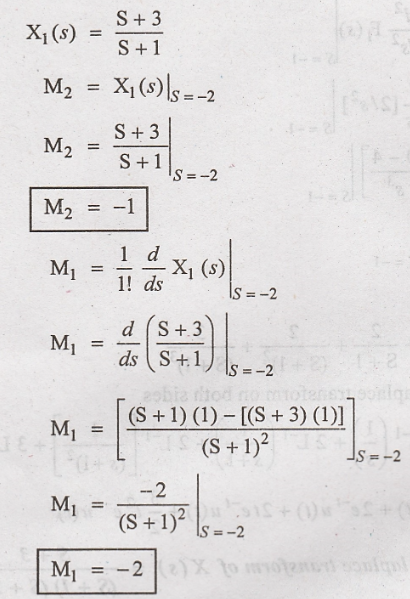
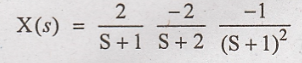
Taking inverse Laplace transform on both sides

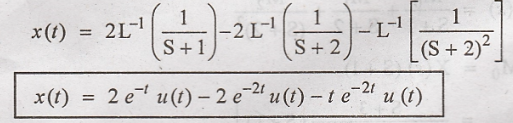
4. Determine the inverse Laplace transform of X(s) =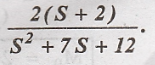 

Solution:

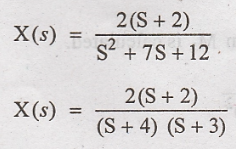
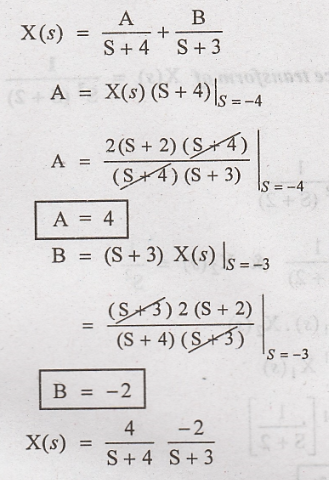
Taking inverse Laplace transform on both sides.

Inverse Laplace Transform using Convolution Integral

If L[x₁(t)] = X₁(s) and L[X₂(t)] = X₂(s), then according to convolution theorem

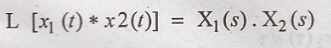
If X(s) is expressed as the product of X₁(s) and X₂(s)

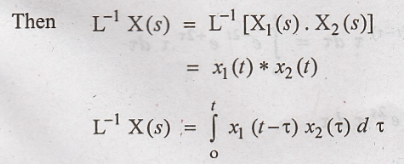
Problems

1. Find inverse Laplace transform of X(s) = 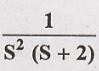 using convolution integral.

Solution:

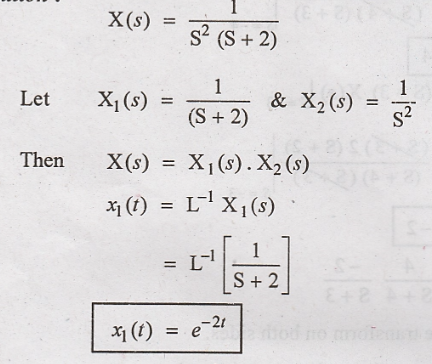
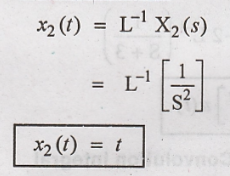
Convolution of and x₁(t) and x₂(t) gives the value of x(t)

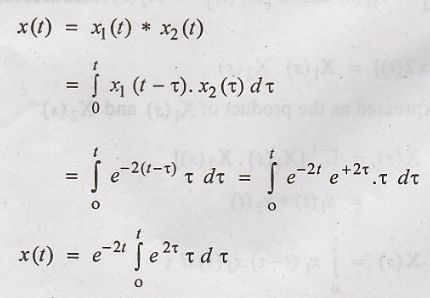
using Integration by parts.

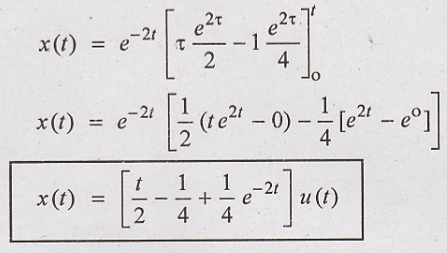
2. Determine the inverse Laplace transform of using 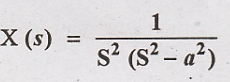convolution theorem.

Solution:

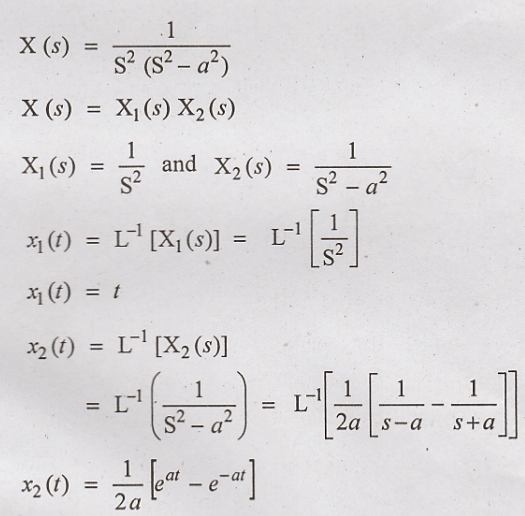
Convolution of x₁(t) and x₂(t) gives the value of x(t)