Signals and Systems: Unit II: Analysis of Continuous Time Signals,,
Introduction of Continuous Time Signals
Representation of Fourier Series
A signal is said to be a continuous-time signal if it is available at all Instants of time. The analysis of a signal is far more convenient in the frequency domain. There are three important cases of transformation methods available for continuous-time systems.
ANALYSIS
OF CONTINUOUS TIME SIGNALS
INTRODUCTION
A signal is said to be
a continuous-time signal if it is available at all Instants of time. The
analysis of a signal is far more convenient in the frequency domain. There are
three important cases of transformation methods available for continuous-time
systems. They are
1. Fourier series
2. Fourier Transform
3. Laplace Transform
Out of these three
methods, the Fourier series is applicable only to periodic signals. ie, signals
which repeat periodically over - ∞ < t < ∞.
Not all periodic signal
can be represented by Fourier series. In this chapter, we discuss the
conditions to be satisfied for a periodic signal to be represented by Fourier
series, different types of Fourier series representations, conversion from one
type to other and analysis of symmetry present in the waveforms are also
discussed and their utilization of simplifying the computations is illustrated.
REPRESENTATION
OF FOURIER SERIES
The Fourier analysis is
also sometimes called the harmonic analysis Fourier series is applicable only
for periodic signals. It cannot be applied to non-periodic signals. A periodic
signal is one which repeats itself at regular intervals of time, i.e.
periodically over -∞ to ∞.
The representation of
signals over a certain interval of time in terms of the linear combination of
orthogonal functions is called Fouries series. Three important classes of
Fourier series methods are available. They are
i. Trigonometric form
ii. Cosine form
iii. Exponential form.
If the orthogonal
functions are trigonometric functions, then it is called trigonometric Fourier
series
If the orthogonal
function are exponential function, then it is called exponential Fourier
series.
Existense of Fourier Series
For the Fourier series
to exist for a periodic signal. It must satisfy certain conditions. The
conditions under which a periodic signal can be represented by a Fourier series
are known as Dirichlet's conditions. They are as follows.
i. The function x(t)
must be a single valued function.
ii. The function x(t)
has only a finite number of maxima and minima.
iii. The function x(t)
has a finite number of discontinuities.
iv. The function x(t)
is absolutely integrable over one period, that is 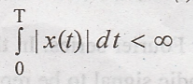
Signals and Systems: Unit II: Analysis of Continuous Time Signals,, : Tag: : Representation of Fourier Series - Introduction of Continuous Time Signals
Related Topics
Related Subjects
Signals and Systems
EC3354 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
