Random Process and Linear Algebra: Unit V: Linear Transformation and Inner Product Spaces,,
Inner Product spaces - Orthonormal projection
Problems about Inner Product spaces - Orthonormal projection
(d) Inner
product spaces - Orthonormal projection
Problem 1.
In each of the
following parts, find the orthogonal projection of the given vector on the
given subspace W of the inner product space V.
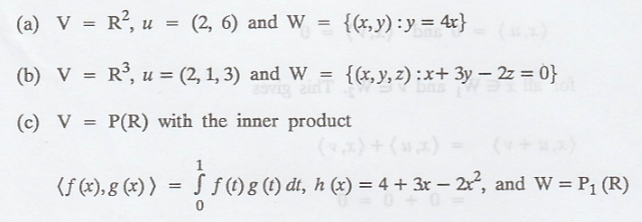
Find the distance from
the given vector to the subspace W.
Solution
:
Let V be an inner
product space and W be the subspace of V.
(a) Let the vector
space V = R2, vector u = (2, 6) and subspace W = {(x, y): y = 4x}.
Find the orthogonal
projection of the vector u on the subspace W as follows.
We know that, the
orthogonal projection of u is <u, v1> v1
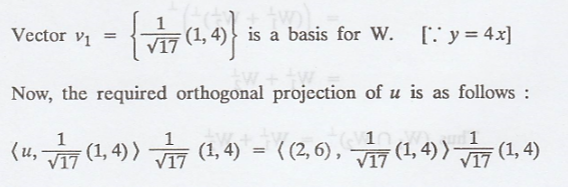
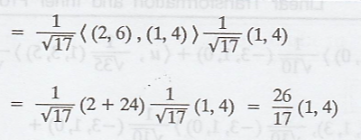
Thus, the required
orthogonal projection of u is 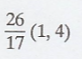
Suppose, v is the
orthogonal projection of u, then the required distance of the given vector u to
the subspace W is the length of u - v.
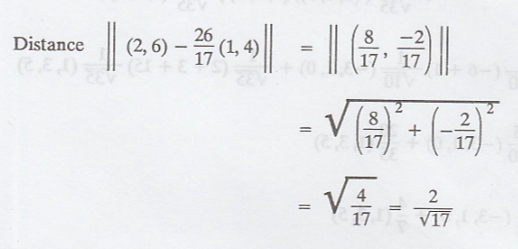
(b) Let the vector
space V = R3, vector u = (2, 1, 3) and subspace,
W = {x, y, z : x + 3y -
2z = 0}}
Find the orthogonal
projection of the vector u on the subspace W
We know that the
orthogonal projection of u is
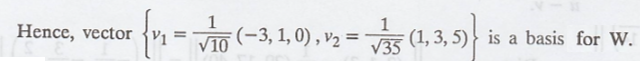
Now, the required
orthogonal projection of u is as follows:
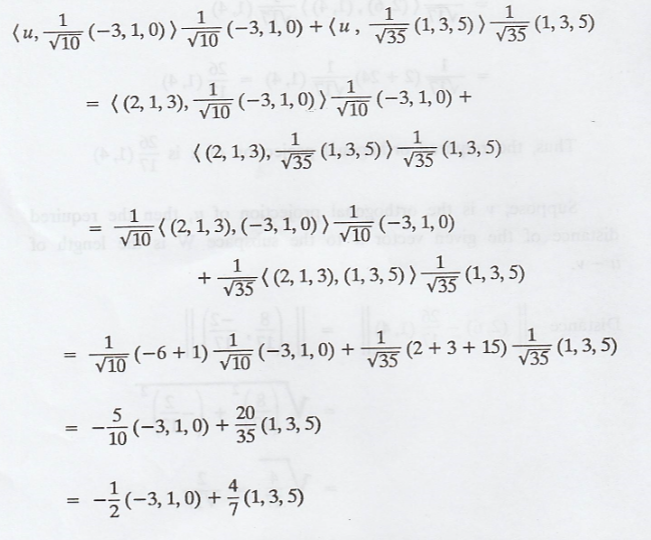
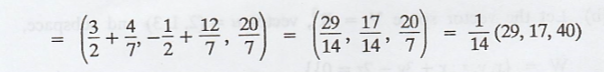
Thus, the orthogonal
projection of u is 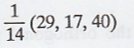
Suppose v is the
orthogonal projection of u, then the required distance of the given vector u to
the subspace W is the length of u - v.
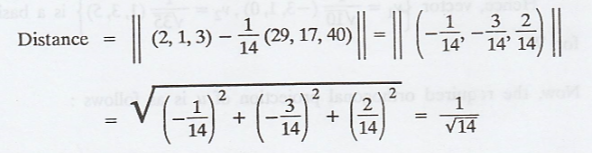
(c) Let vector space V
= P(R), with the inner product.
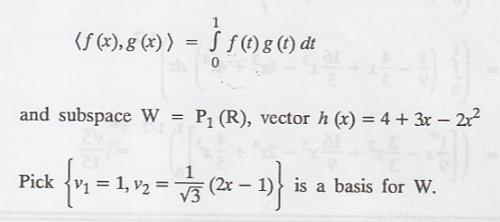
Now, the required
orthogonal projection of h is as follows:
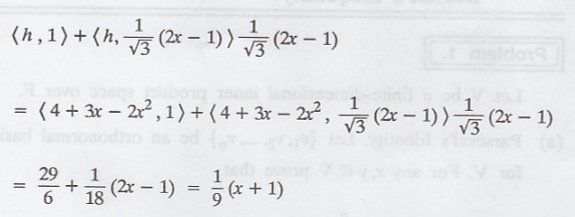
Thus, the orthogonal
projection of u is 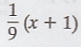
Suppose V is the
orthogonal projection of g, then the required distance of the given vector g to
the subspace W is the length of g - v
Hence,
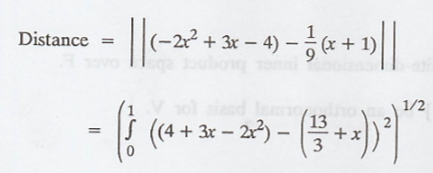
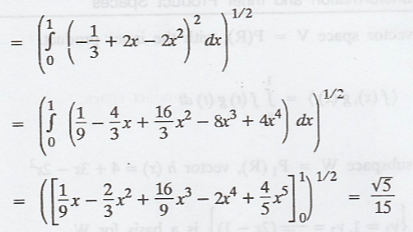
Random Process and Linear Algebra: Unit V: Linear Transformation and Inner Product Spaces,, : Tag: : - Inner Product spaces - Orthonormal projection
Related Topics
Related Subjects
Random Process and Linear Algebra
MA3355 - M3 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
