Signals and Systems: Unit II: Analysis of Continuous Time Signals,,
Important 2 marks Questions with Answers
Anna University important 2 mark questions with answers
Important
2mark Questions with Answers
UNIT 2: ANALYSIS OF
CONTINUOUS TIME SIGNALS
1. Define Fourier
series
Continuous time Fourier
series is defined as
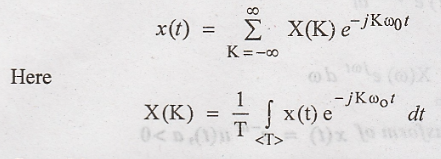
2. State Dirichlet
conditions for Fourier series.
(i) The function x(t)
should lie within the interval T0
(ii) Function x(t)
should be absolutely integrable.
(iii) Function x(t)
should have finite number of maxima and minima within the interval T0
(iv) Function x(t)
should have finite number of discontinuities in the interval T0.
3. What do the Fourier
series co-efficients represent?
Fourier series
co-efficient represents various frequency components present in the signal.
4. What are the
differences between Fourier series and Fourier transform.

5. What is the
relationship between Laplace transform and Fourier transform.
Fourier transform is
same as Laplace transform if S = jω
X(s) = X(jω)
6. Write the Fourier
transform pair for x(t)

7. Find the Fourier
transform of x(t) = e – a t u(t), a > 0
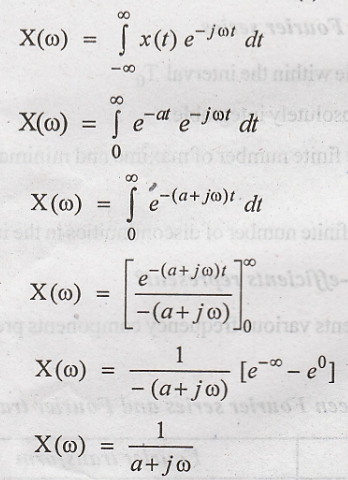
8. What is the Laplace
transform of the function x(t) = u(t) – u(t-2)?
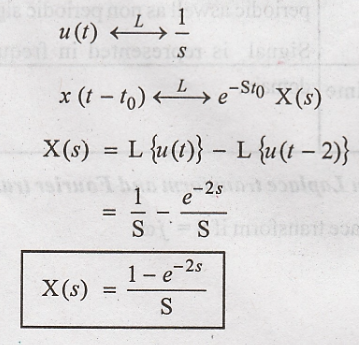
9. Find the laplace
transform of the signal, u(t)
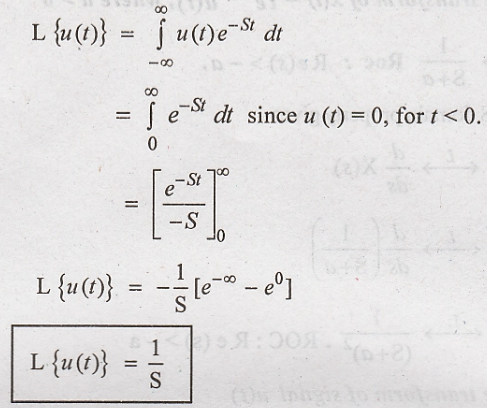
10. State the Initial
and final value theorem of Laplace transform.
Initial value theorem
Initial value of x(t)
is given as
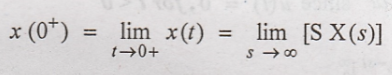
Final value of x(t) is
given as
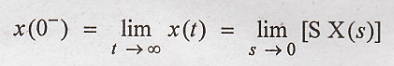
11. State equation for
trignometric Fourier series.
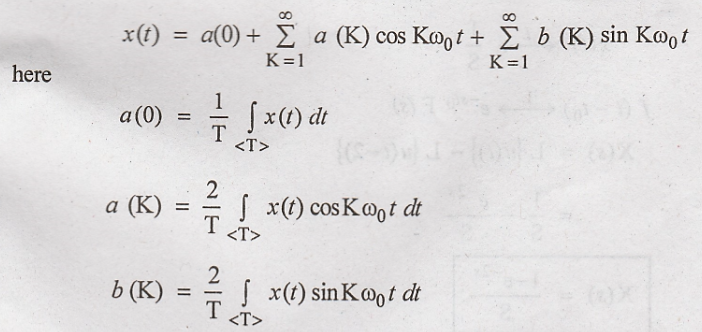
12. Find the Laplace
transform of x(t) = t e – a t u(t), where a > 0
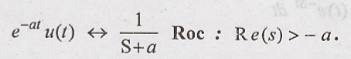
Differentiation in S
domain property gives
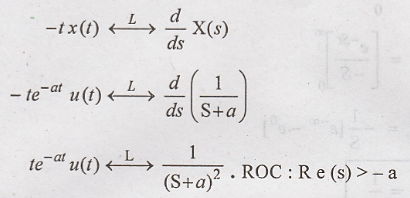
13. Find the Laplace
transform of signal u(t)
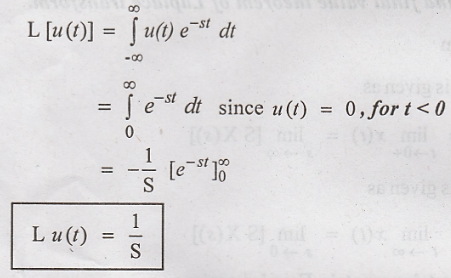
14. What is the Laplace
transform of the function x(t) = u(t) - u(t-2)

15. Obtain the Fourier
series co-efficients for
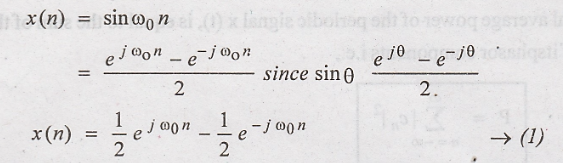
Discrete time Fourier
series Fourier series
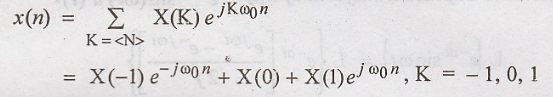
Comparing above
equation with (1)
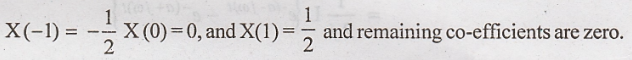
16. State the time
scaling property of Laplace transform
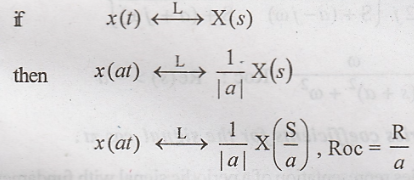
Expansion in time
domain is equivalent to compresion, in frequency domain.
17. Define the ROC of
the Laplace transform.
The area in the S-plane
where Laplace transform exists is called region of convergence.
18. Determine the
Laplace transform of δ(t-5) and u(t-5)
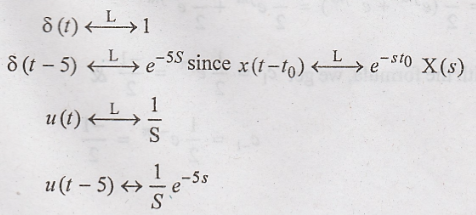
19. Define Parseval's
relation for continuous time periodic signal.
Total average power of
the periodic signal x(t), is equal to the sum of the average powers of its phasor
components i.e.,
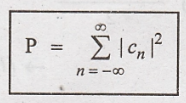
20. Determine Laplace
transform of x(t) = e – a t sin (ωt) a(t).
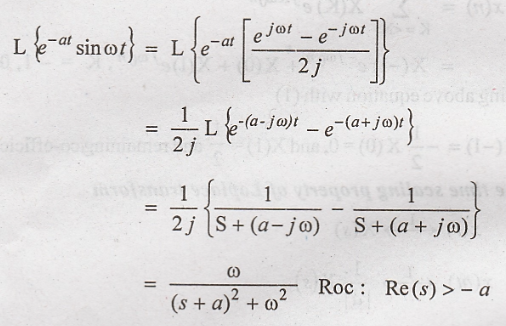
21. Determine the
Fourier series coefficients for the signal cos πt.
The complex Exponential
series representation of a periodic signal with fundamental T0 is
given by,
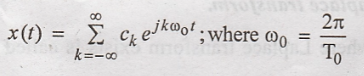
To evaluate the complex
Fourier coefficients of cоs πt, we can Euler's formula.
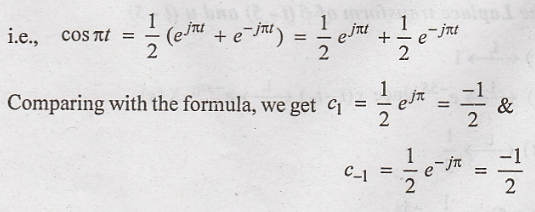
22. Determine the LT of
the signal δ(t-5) & u(t-5). [May '12]
Using time-shifting
property LT, 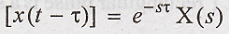
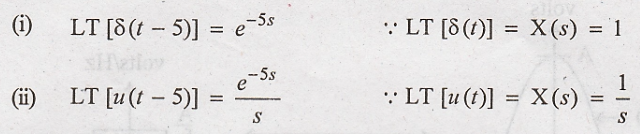
23. What is the FT of a
DC signal of amplitude 1? [May'13]
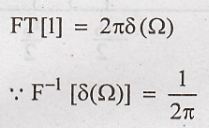
24. Find the Fourier
coefficients 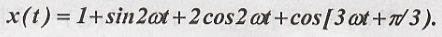 [may'15] (R 13)
[may'15] (R 13)
Expanding x(t) terms of
complex exponentials,
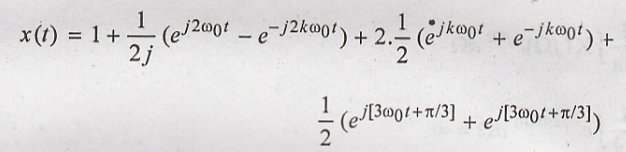
Collecting terms we
get,
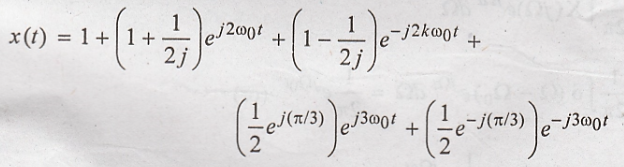
Thus, the Fourier
coefficient are,
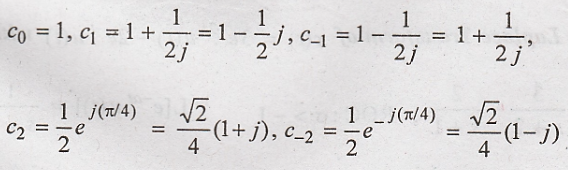
25. Draw the spectrum
of a CT rectangular pulse. [May'15]
The spectrum a CT
rectangular pulse is a sinc function
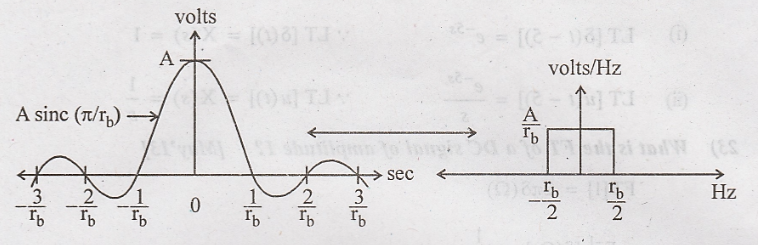
26. Given 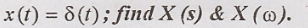 [May '15]
[May '15]
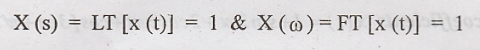
27. What is the inverse
Fourier Transform of 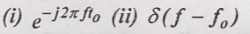 [May'16]
[May'16]
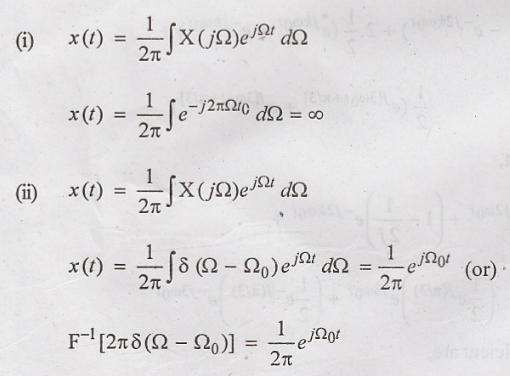
28. Give the Laplace
Transform of x(t) = 3e – 2 t u(t) - 2e - t u(t) with ROC.
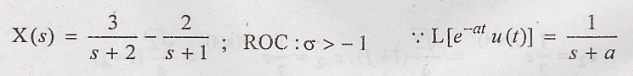
29. Draw the single
sided spectrum for x(t) = 7 + 10 cos [40 πt + π/2]. [Nov '11]
Expanding x(t) into
complex sinusoid pairs,
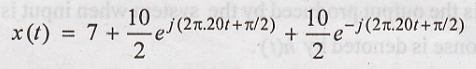
The frequency pairs
that define the two-sided line spectrum are 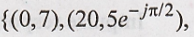
30. State the
convergence series representation of CT periodic signals. [Nov '14]
Most of the results
presented for 2π - periodic functions extend easily to functions 2L- periodic
functions. So we only discuss the case of 2π - periodic functions.
Definition. The
function f(X) defined on [a, b], is said to be piecewise continuous if and only
if, there exits a partition {X1, X2,...Xn} of
[a, b] such that
(i) f(x) continuous on
[a, b] except be for the points Xi,
(ii) The right-limit
and lest-limit of f(X) at the points Xi exist.
31. Find the ROC of the LT of x(t) = u(t). [Nov' 14] (R 13)
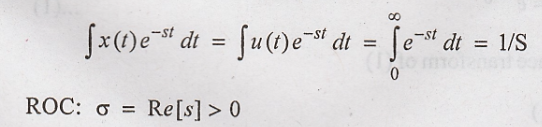
Signals and Systems: Unit II: Analysis of Continuous Time Signals,, : Tag: : - Important 2 marks Questions with Answers
Related Topics
Related Subjects
Signals and Systems
EC3354 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
