Crystal Oscillators

CRYSTAL OSCILLATORS

Fig. 4.17 shows a crystal controlled oscillator circuit. Here it is a Colpitt's crystal oscillator in which the inductor is replaced by the crystal. In this type a Piezo-electric crystal, usually quartz is used as a resonant circuit replacing an LC circuit.

The crystal is a thin slice of Piezo-electric material, such as quartz, tourmaline and rochelle salt, which exhibit a property called Piezo-electric effect.

The Piezo electric effect represents the chracteristics that the crystal reacts to any mechanical stress by producing an electric charge. In the reverse effect, an electric field results in mechanical strain.

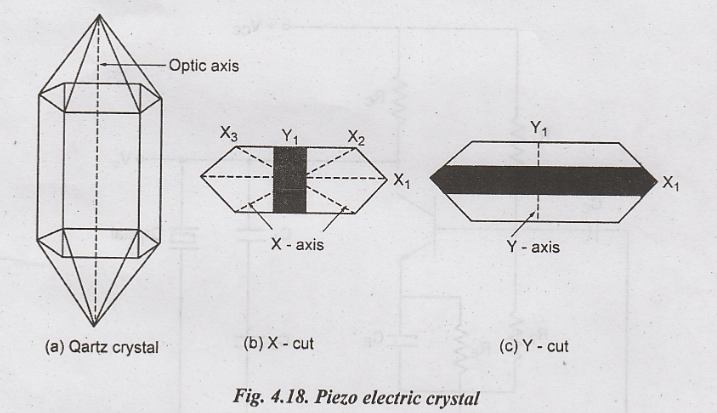
Quartz Crystal Construction

In order to obtain high degree of frequency stability, crystal oscillators are essentially used. Generally, the crystal is a ground wafer of translucent quartz or tourmaline stone placed between two metal plates and housed in a stamp sized package. There are two different methods of cutting this crystal wafer from the crude quartz. The method of cutting determines the natural resonant frequency and temperature coefficient of crystal. When the wafer is cut in such a way that is flat surfaces are perpendicular to its electrical axis (x-axis), it is called an x-cut crystals as shown in Fig. 4.18 (b) when the wafer is cut in such a way that its flat surfaces are perpendicular to its mechanical axis (y-axis), it is called y-cut crystal as shown in Fig. 4.18 (c).

If an alternating voltage is applied, then the crystal wafer is set into vibration. The frequency of vibration equal to the resonant frequency of the crystal is determined by its structural characteristics. If the frequency of the applied ac voltage is equal to the natural resonant frequency of the crystal then the maximum amplitude of vibration will be obtained.

In general, the frequency of vibration is inversely proportional to the thickness of the crystal.

The frequency of vibration is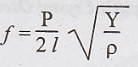 

Where Y - young modulus

ρ - density of the material

and P - 1, 2, 3, ...

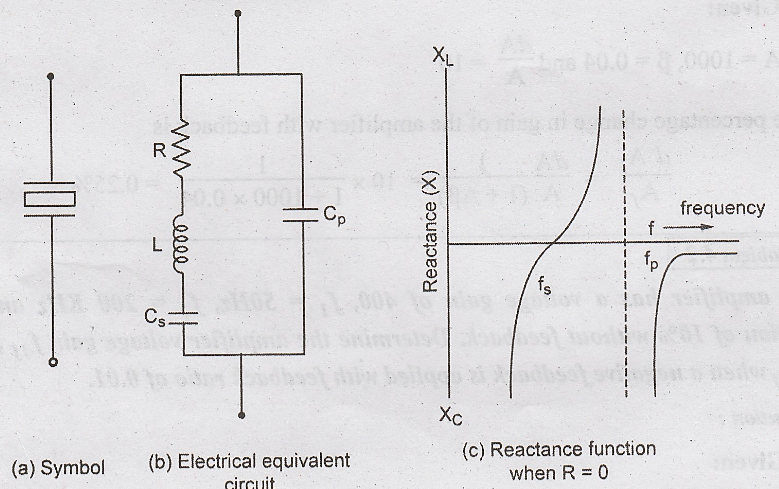
The crystal is suitably cut and polished to vibrate at a certain frequency and mounted between two metal plates as shown in Fig.4.19 (a)

The equivalent circuit of the crystal is shown in Fig. 4.19 (b)

The ratio of C_p to C_S may be several hundred or more so that series resonance frequency is very close to parallel resonant frequency. The resonant frequency is inversely proportional to the thickness of the crystal.

Resonant frequencies from 0.5 to 30 MHz can be obtained.

The reactance function shown in Fig. 4.19 (c)

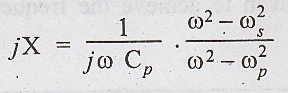
Neglecting R, here 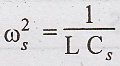 is the series resonant frequency and

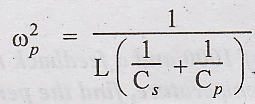 is the parallel resonant frequency

Since C_P >> C_S, 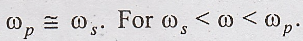 The reactance is inductive and for ω out of the above range, it is capacitive.

For crystal Hartley oscillator the capacitors C₁ and C₂ shown in in Fig. 4.17 are replaced with inductors L₁ and L₂ respectively. So that the reactance is capacitive, hence its oscillation frequency is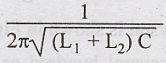 

Advantages         

The advantages of the crystal is its very high Q as a resonant circuit, which results in good frequency stability for the oscillator. However since the resonance frequencies of the crystals are temperature dependent, it is necessary to enclose the crystal in a temperature controlled oven to achieve the frequency stability of the order of 1 part in 10¹⁰.