Continuous Time Fourier Transform

CONTINUOUS TIME FOURIER TRANSFORM

Definition of Continuous Time Fourier Transform

Let us consider the continuous time signal x(t). Fourier transform of x(t) is defined as

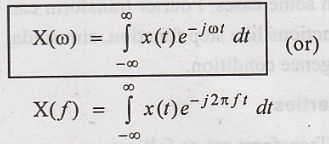
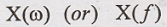 ⇒ Frequency domain representation of the signal.

Inverse Fourier transform

x(t) is obtained by taking inverse transform of X(ω)

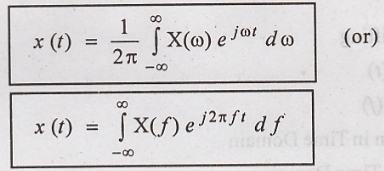
Fourier transform pair

Fourier transform of x(t) is X(ω) .

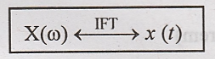
Inverse Fourier transform of X(ω) is x(t).

Existence of Fourier Transform-Dirichlet Condition

The Fourier transform does not exist for all aperiodic functions. The conditions for a function x(t) to have Fourier transform, called Dirichlet's conditions, are:

1. x(t) is absolutely integrable over the interval -∞ to ∞, that is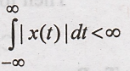 

2. x(t) has a finite number of discontinuities in every finite time interval. Further, each of these discontinuities must be finite.

3. x(t) has a finite number of maxima and minima in every finite time interval.

 

Almost all the signals that we come across in physical problems satisfy all the above conditions except possibly the absolute integrability condition.

Dirichlet's condition is a sufficient condition but not necessary condition. This means, Fourier transform will definitely exist for functions which satisfy these conditions on the other hand, in some cases, Fourier transform can be found with the use of impulses even for functions like step function, sinusoidal function, etc., which do not satisfy the convergence condition.

Fourier Transform Properties

The properties of Fourier Transform are as follows,

(i) Linearity (superposition)

(ii) Duality or symmetry property

(iii) Time shifting

(iv) Frequency shifting

(v) A rea under x(t)

(vi) Area under X(f)

(vii) Differentiation in Time Domain

(viii) Integration in Time Domain

(ix) Conjugate Functions

(x) Multiplication in Time Domain (Multiplication Theorem)

(xi) Convolution in time domain

(xii) Time scaling (Convolution Theorem)

Linearity

Let x₁(t) ↔ X₁(f) represent a fourier transform pair and

x₂(t) ↔ X₂(f) represent another fourier transform pair.

Then for all constants like C₁ & C₂ we have,

To Prove:

Proof:

By the definition of Fourier Transform,

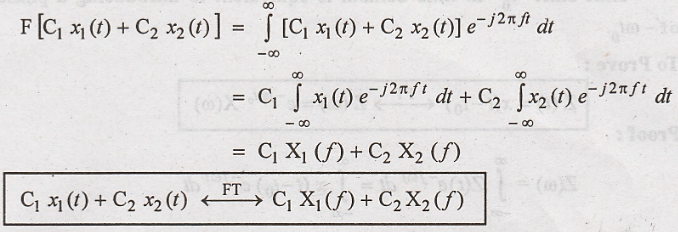
Hence Proved

Duality or Symmetry Property

Duality property of Fourier Transform states that if,

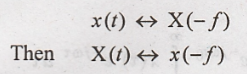
To Prove:

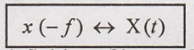
Proof :

By the definition of inverse Fourier transform we have,

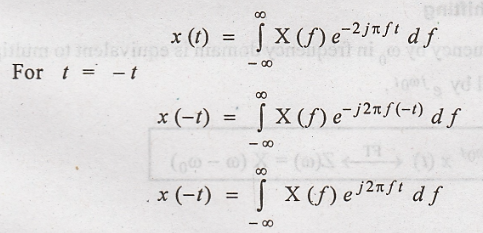
Interchanging 't' and 'f' we get,

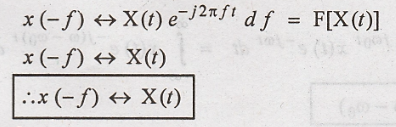
Time Shifting

Time shift "t₀" in time domain is equivalent to introducing a phase shift of -ω₀

To Prove:

Proof :

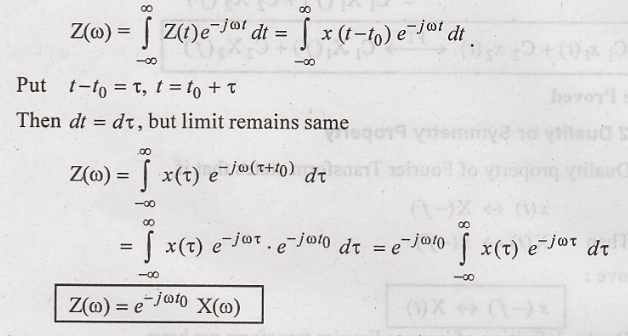
Hence Proved.

Frequency Shifting

Shifting the frequency by ω₀ in frequency domain is equivalent to multiplying the time domain signal by 

To Prove:

Proof :

Hence Proved.

Area Under x(t)

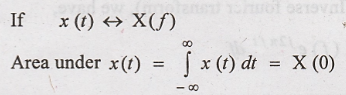
To Prove:

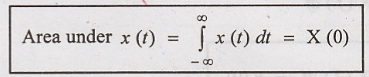
(ie) Area Under x(t) is equal to its Fourier Transform at zero frequency.

Proof :

By definition of Fourier Transform,

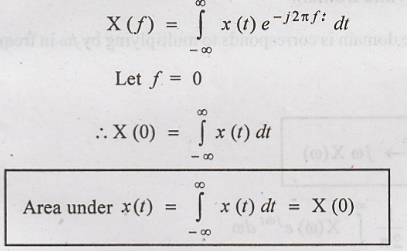
Hence Proved

Area Under X(f)

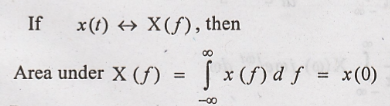
To Prove:

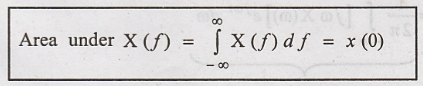
That is, the area Under Fourier transform spectrum of a signal is equal to its value at t = 0

Proof :

By the definition of I F T, (Inverse fourier transform), we have,

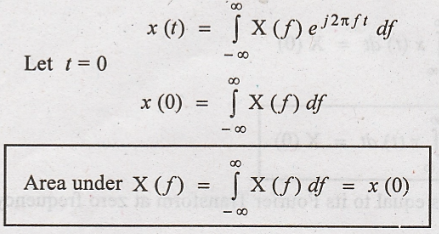
Hence Proved

Differentiation in Time Domain

Differentiation in time domain is corresponds to multiplying by jω in frequency domain.

To Prove:

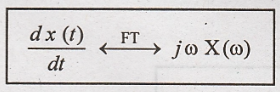
Proof :

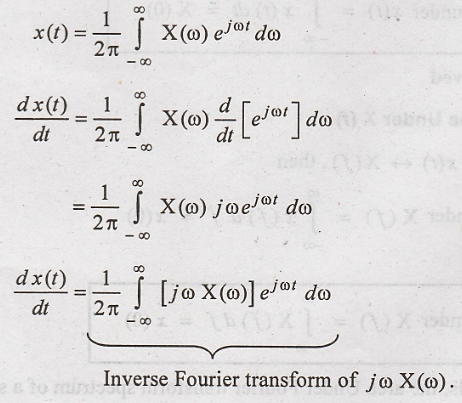
Hence Proved.

Integration in Time Domain

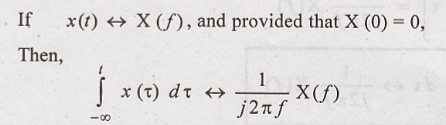
Assuming that X(0) = 0, the integration of x(t) in time domain has the effect of dividing its Fourier transform by (j2πf).

To Prove:

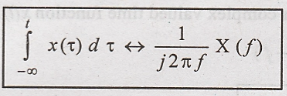
Proof :

Let x(t) be expressed as,

We known that x(t) ↔ X(f)

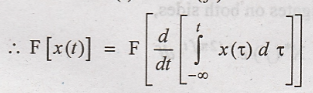
By the property of differentiation,

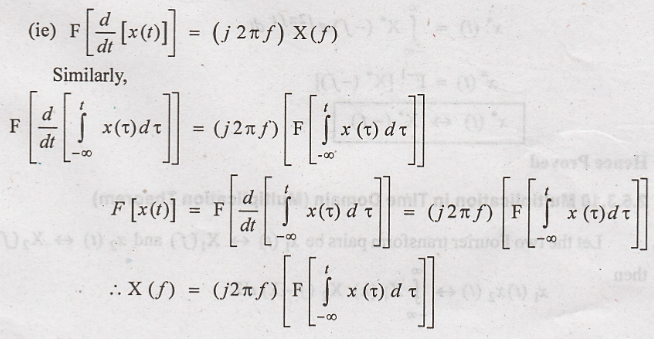
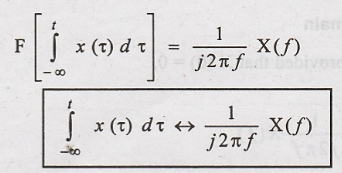
Hence Proved

Conjugate Functions

If, x(t) ↔ X(f) then for complex valued time function x(t), we have,

x*(t) ↔ x*(-f)

To Prove:

x*(t) → x*(-f)

Proof:

By definition of Inverse Fourier Transform,

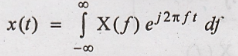
By taking complex conjugates on both sides,

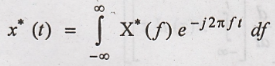
Now, by replacing 'f' by '-f', we get,

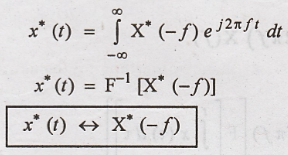
Hence Proved

Multiplication in Time Domain (Multiplication Theorem)

Let the two Fourier transform pairs be x₁(t) ↔ X₁(f) and x₂(t) ↔ X₂(f), then

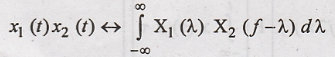
To Prove:

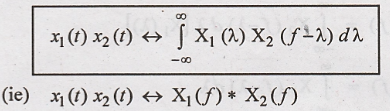
The Multiplication of two signals in "Time domain" is transformed into convolution of their Fourier transforms in "Frequency domain".

Proof:

Consider the RHS of the above equation, (ie)

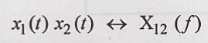
In other words we have,

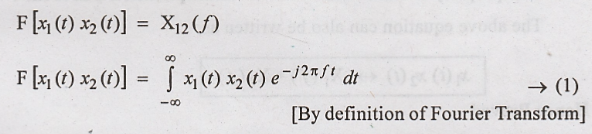
[By definition of Fourier Transform]

We know that, x₂(t) can be written by Inverse Fourier Transform as,

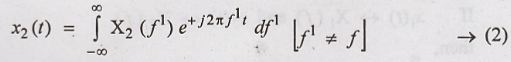
Substitute equation (2) in equation (1), we get,

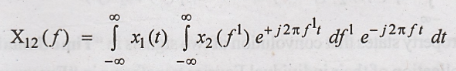
Let us consider λ = f – f ¹ then by rearranging the above equation,

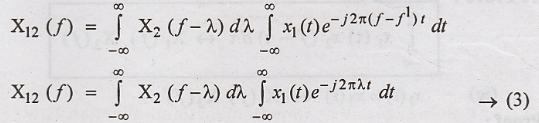
By the definition of Fourier transform we have,

Substituting equation (4) in equation (3), we get,

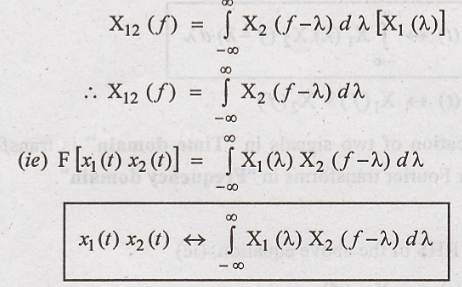
Hence Proved

This property is sometimes called as "Multiplication Theorem".

The above equation can also be written as,

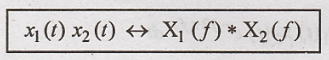
Hence Proved

Convolution in Time Domain (Convolution Theorem)

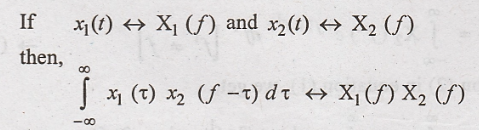
This property states that convolution of two signals in "Time domain" is transformed into multiplication of their individual Fourier transforms in "Frequency domain".

To Prove:

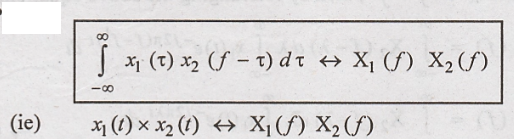
Proof :

Convolution of x₁(t) and x₂(t) is given as,

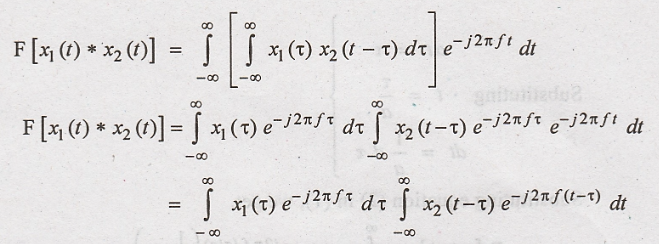
Let t - τ = α in second integral of the above equation,

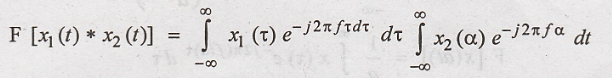
From the definition of Fourier transform, the right hand side of the above equation can be written as follows,

Hence Proved

Time Scaling

Let x(t) & X(f) be a Fourier transform pair and 'a' is some constant.

Then by time scaling property,

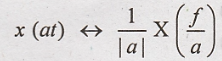
To Prove:

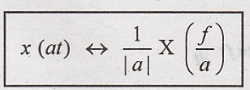
Proof:

By the definition of Fourier transform, we have,

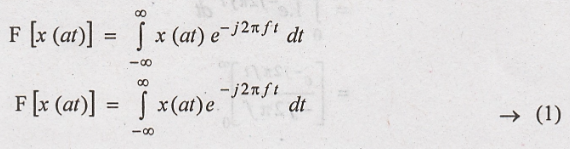
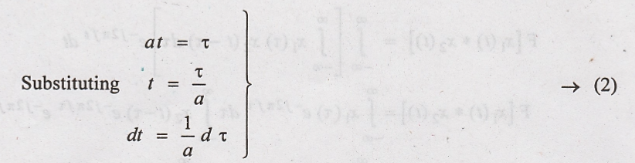
Substituting equation (2) in (1), we get.

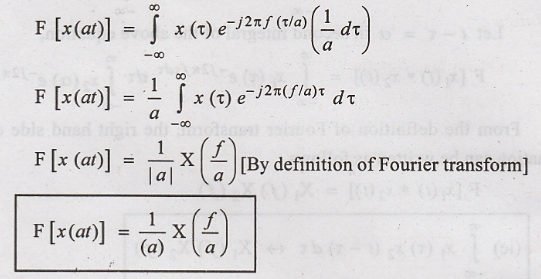
Hence Proved