Signals and Systems: Unit II: Analysis of Continuous Time Signals,,
Continuous Time Fourier Series
Cosine Fourier Series, Exponential Fourier Series
Discuss about Evaluation of Fourier Coefficients of the Trigonometric Fourier Series, Cosine Fourier Series, Exponential Fourier Series
CONTINUOUS
TIME FOURIER SERIES
Trigonometric Form of Fourier Series
The prove that the
signal x(t), which is a summation of sine and cosine functions of frequencies
0, ω0, 2ω0,...kω0, is a periodic signal with
period T. By changing ans and bns, we can construct any
periodic signal with period T. If k → ∞ in the expression for x(t), we obtain
the fourier series representation of any periodic signal x(t). That is, any
periodic signal can be represented as an infinite sum of sine and cosine
functions which themselves are periodic signals of angular frequencies 0, ω0,
2αω0,..., kω0, this set of harmonically related sine and
cosine function, i.e., sin nω0 t , and cos nω0 t , n = 0,
1, ... forms a complete orthogonal set over the interval t0 to t0+T
where T = 2π/ω0.
The infinite series of
sine and cosine terms of frequencies 0, ω0, 2αω0,..., kω0,
is known as trigonometric form of Fourier series and can be written as:
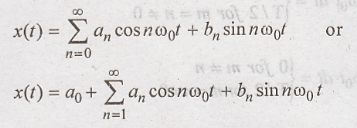
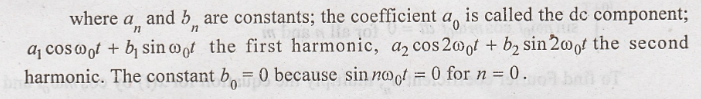
Evaluation of Fourier Coefficients of the Trigonometric Fourier
Series
The constants 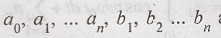 are called Fourier coefficients. To evaluate a0, we
shall integrate both sides of the equation for x(t) over one period (t0+T)
at an arbitrary time to thus,
are called Fourier coefficients. To evaluate a0, we
shall integrate both sides of the equation for x(t) over one period (t0+T)
at an arbitrary time to thus,

we know that 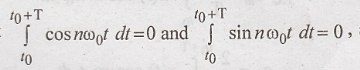 since the net areas of sinusoids over complete periods are zero
for any non zero integer n and any time t0. Hence each of the integrals in the
above summation is zero.
since the net areas of sinusoids over complete periods are zero
for any non zero integer n and any time t0. Hence each of the integrals in the
above summation is zero.
Thus, we obtain
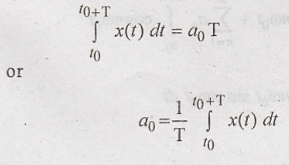
To evaluate an
and bn, we can use the following results.
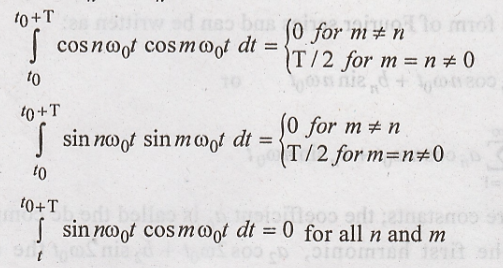
To find Fourier
coefficient an, multiply the equation for x(t) by cos mω0t
and integrate over one period. that is,
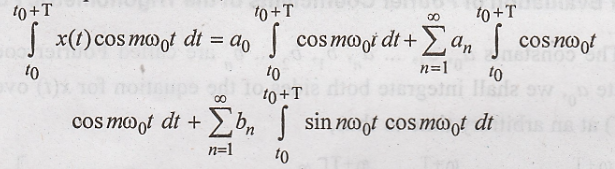
The first and third
integrals in the above equation are equal to zero and the second is equal to
T/2 where m = n. Therefore,
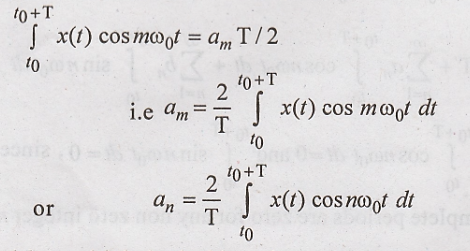
To find bn
multiply both sides of equation for x(t) by sin mω0t and integrate
over one period. Then
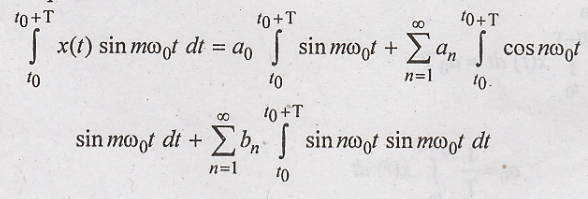
The first and second
integrals in the above equation are zero, and the third integral is equal to
T/2 when m = n. Thus, we have

a0, an
and bn are called trigonometric fourier series coefficients.
A periodical signal has
the same Fourier series for the entire interval -∞ to ∞ as for the interval t0
to t0+T, since the same function repeats after every T seconds. The
Fourier series expansion of a periodic function is unique irrespective of the
location of t0 of the signal.
Problems
1. Find the Fourier
series expression of the half wave rectified sine wave shown in figure.
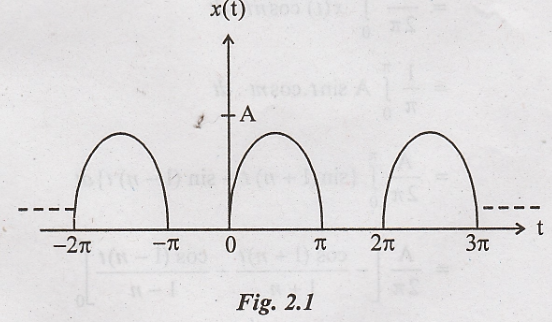
Solution:
The periodic waveform
shown in figure with period T = 2π
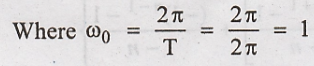
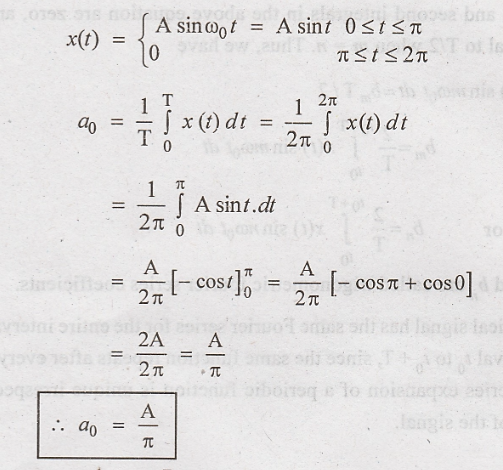
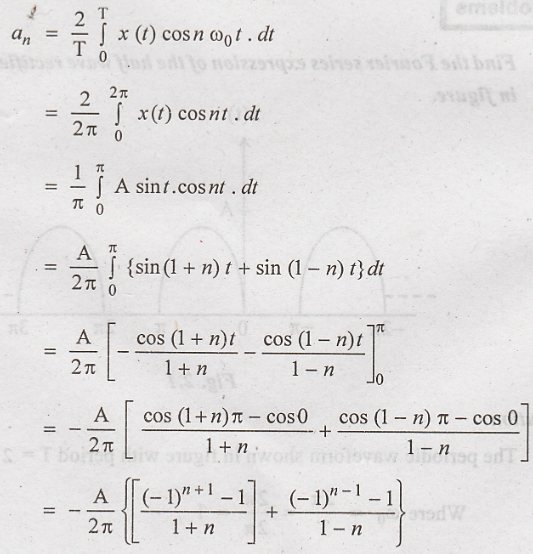
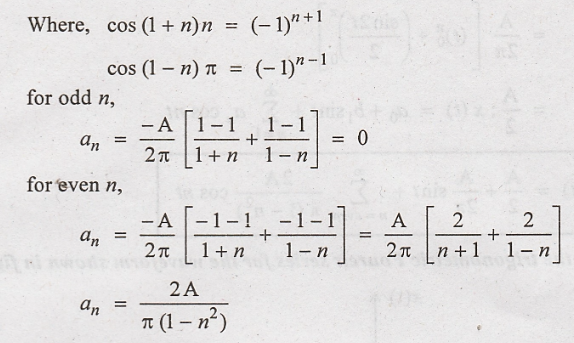
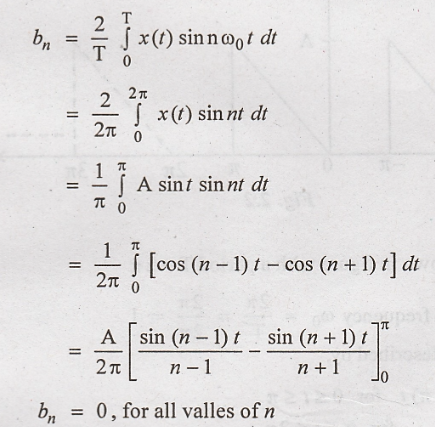
Therefore, the
trigonometric Fourier series is :
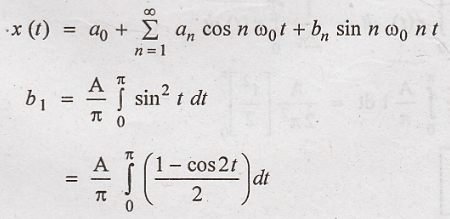
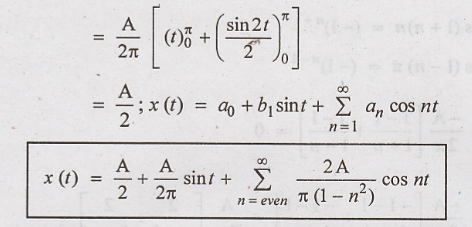
2. Obtain the
trigonometric Foureir series for the waveform shown in figure.

Solution
:
The waveform shown in
figure with a period T = 2 π
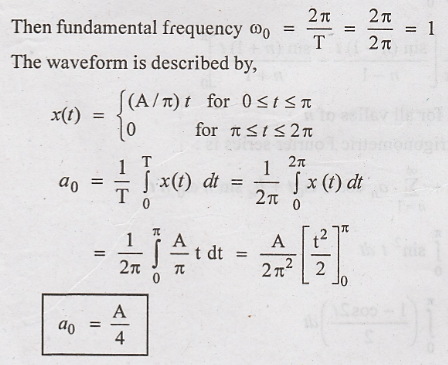
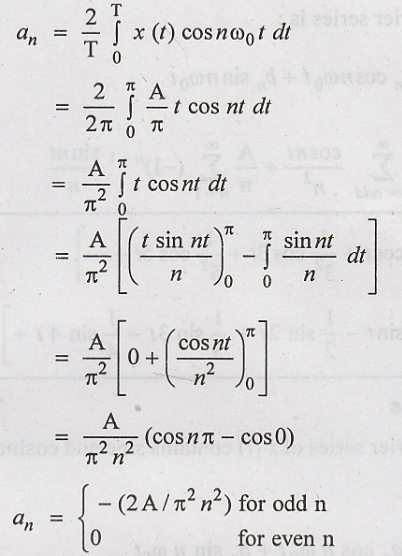
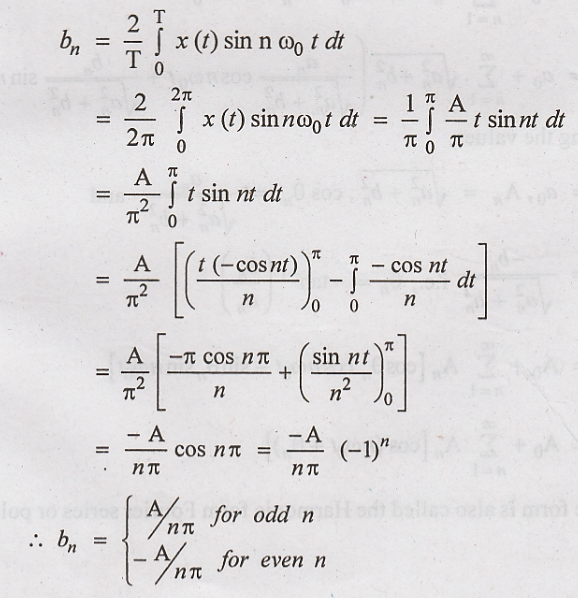
Thetrigonometic Fourier
series is :
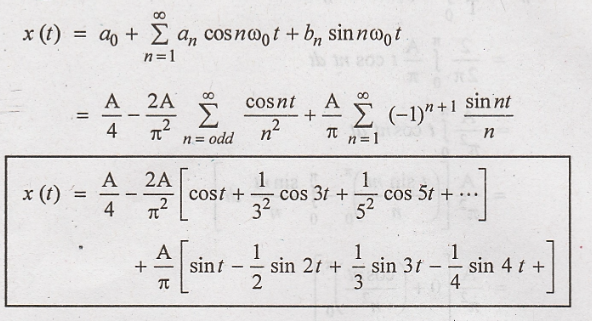
Cosine Fourier Series
The trigonometric
Fourier series of x(t) contains sine and cosine terms of the same frequency.
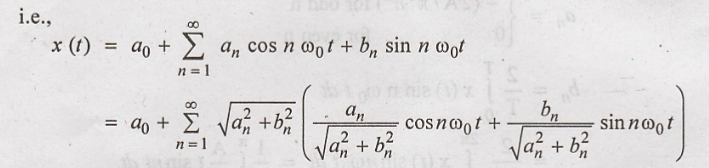
Substituting the
values,
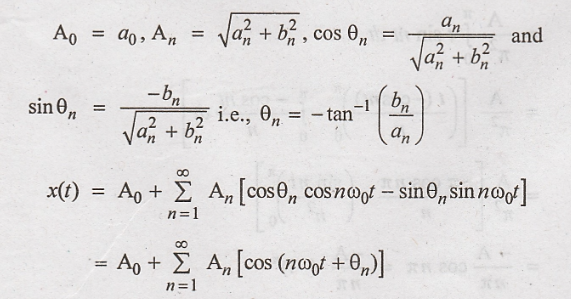
The cosine form is also
called the Harmonic form Fourier series or polar form Fourier series.
Problem 1:
Find the cosine Fourier
series for the waveform shown in figure.
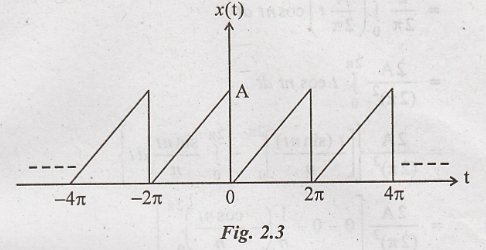
Solution:
The waveform is given
by

Trigonometric Fourier
series
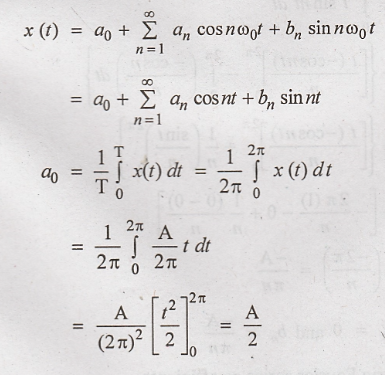
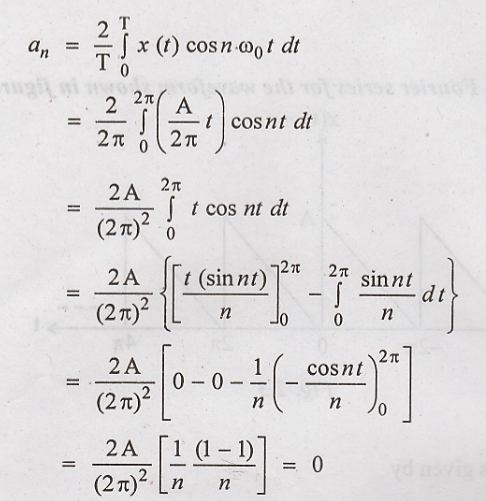
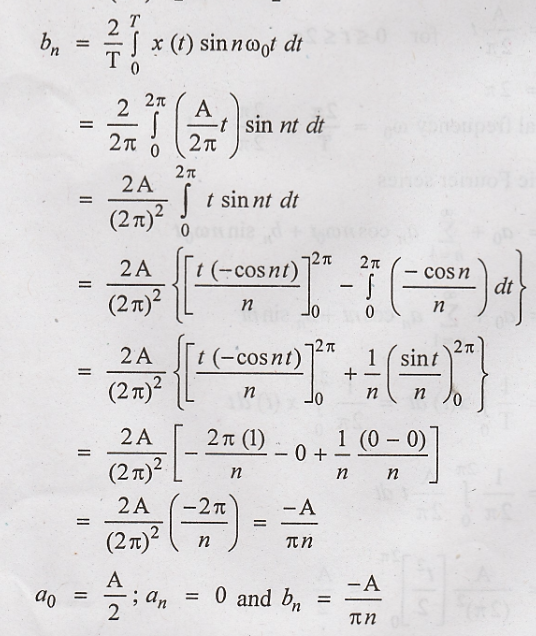
are the trigonometric
Fourier series co efficients.
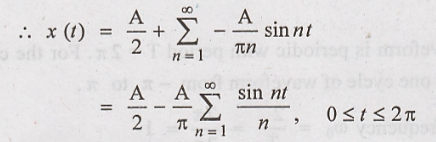
Cosine form of
Representation

Note:
When even or minor symmetry
exists, the trigometric Fourier series coefficient are,

Problem 1:
Find the Fourier series
expression for the waveform shown in figure.
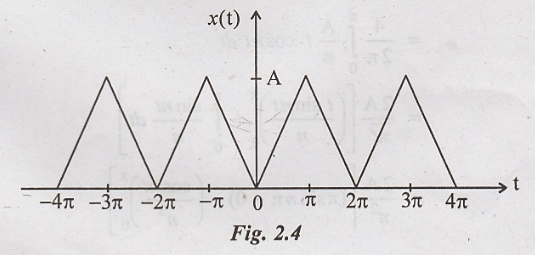
Solution:
The given waveform is
periodic with period T = 2π. For the computational convenience choose one cycle
of waveform from -π to π.
Fundamental frequency 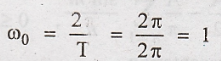
The waveform is
described by,
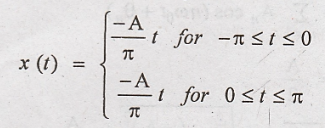
The given waveform has
even symmetry because x(t) = x(− t)
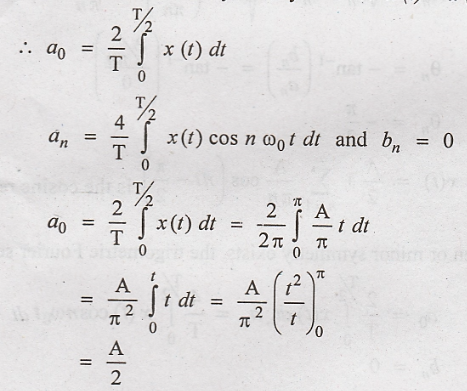
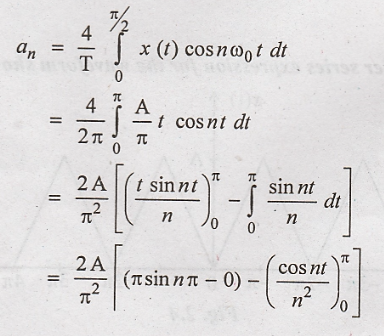
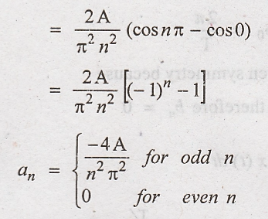
The trigometric Fourier
series is,
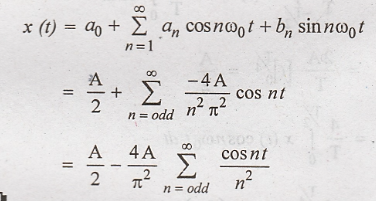
Problem 2:
Obtain the Fourier
components of the periodic rectangular waveform shown in figure

Solution:
The waveform shown in
figure is a periodic waveform with period T.
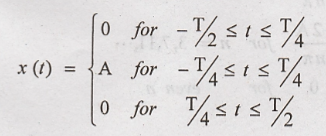
Fundamental frequency ω0
= 2π/T
The given function has
even symmetry because
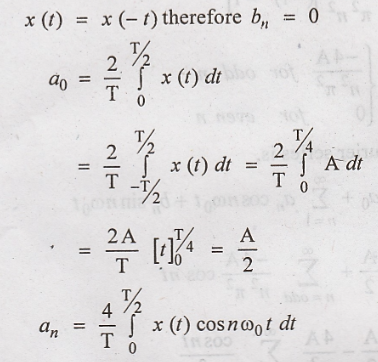
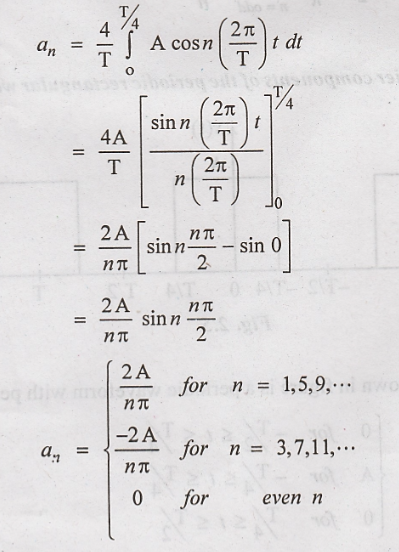
The trigonometric
Fourier series is :
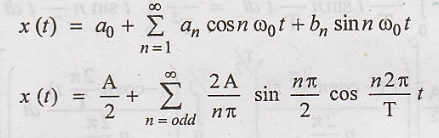
Odd
or Rotation Symmetry:
When odd or rotation
symmetry exists, the trigonometric Fourier series coefficients are:
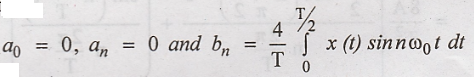
Problem 1:
Obtain the
trigonometric fourier series for the waveform shown in figure.
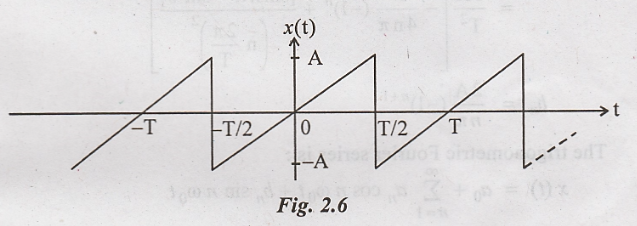
Solution:
The waveform shown in
figure is periodic with period = T. For computational sim plicity. Consider the
period from -T/2 to T/2
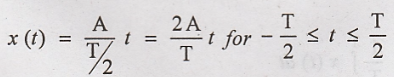
Fundamental frequency ω0 = 2π/T
The waveform has odd
symmetry because x(t) = -x(-t)
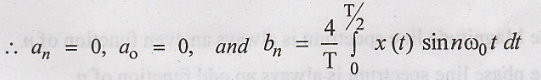
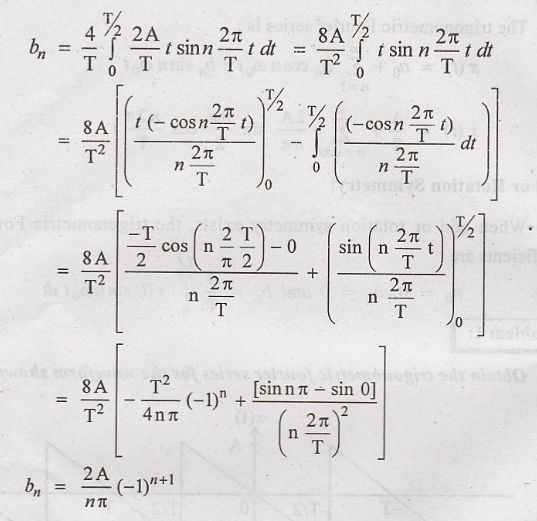
The trigonometric
Fourier series is :
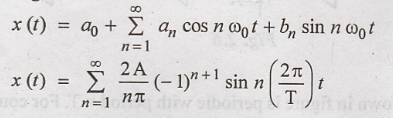
Exponential Fourier Series
The function x(t) is
expressed as a weighted sum of the complex exponential functions.
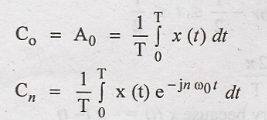
Note:
1. The Magnitude line
spectrum is always an even function of n.
2. The phase line
spectrum is always an odd function of n.
Problem 1:
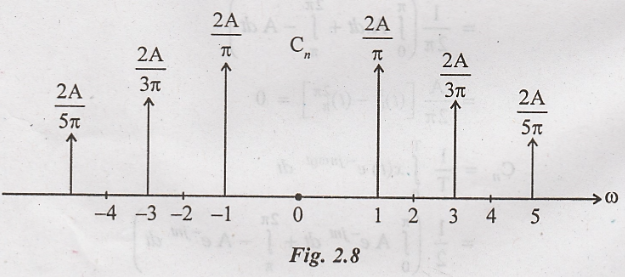
Obtain the exponential
Fourier series for the waveform shown in figure. Also draw the frequency
spectrum.
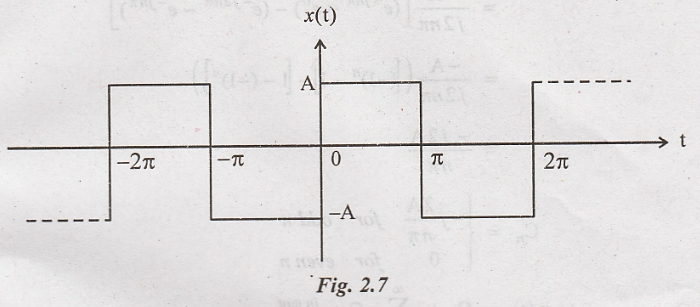
Solution:
The periodic waveform
shown in figure with a period T=2π can be expressed as:
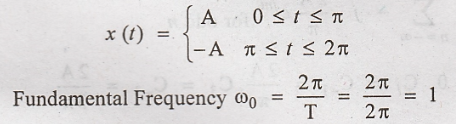
Exponential
Fourier series :
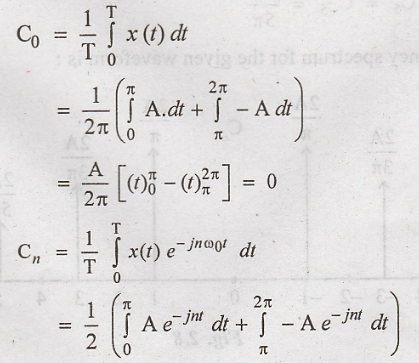
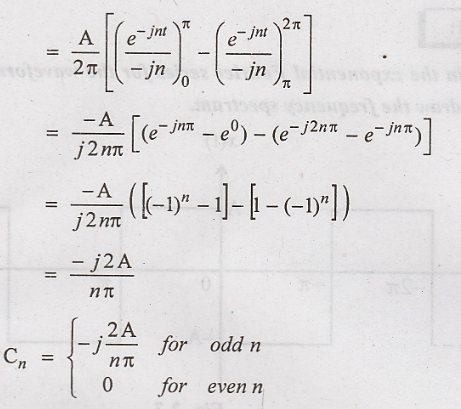
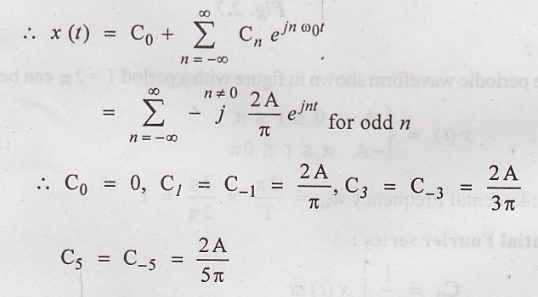
The Frequency spectrum
for the given waveform is :
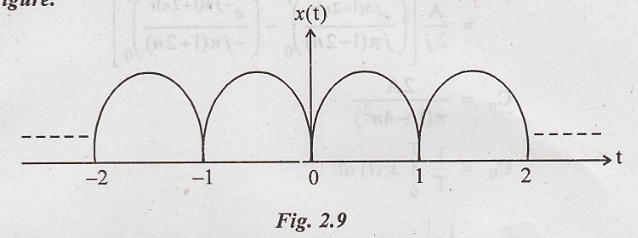
Problem 2:
Find the exponential
Fourier series for the rectified sine wave shown in figure.
Solution:
The waveform shown in
figure with a period T = 2
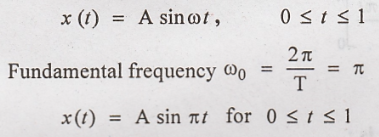
The period of rectified
sine wave is T = 1
The fundamental
frequency of the rectified
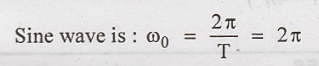
The
exponential Fourier series:
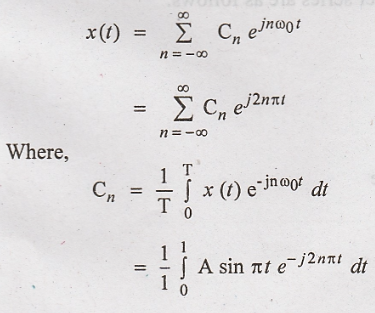
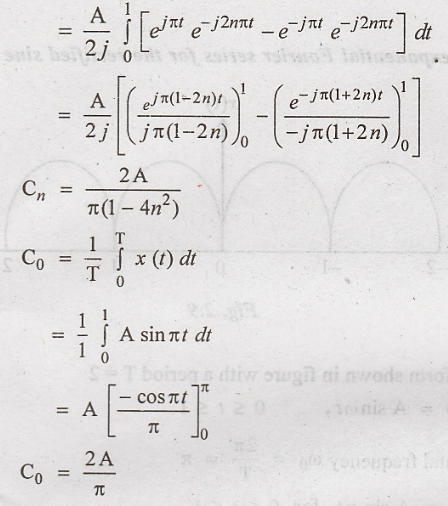
The exponential Fourier
series is :
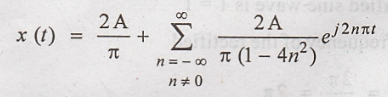
Signals and Systems: Unit II: Analysis of Continuous Time Signals,, : Tag: : Cosine Fourier Series, Exponential Fourier Series - Continuous Time Fourier Series
Related Topics
Related Subjects
Signals and Systems
EC3354 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
