Signals and Systems: Unit IV: Analysis of Discrete Time Signals,,
Z Transform
Properties of z transform
Discuss about the z transform and properties of z transform
THE Z TRANSFORM
Z Transform
z
Transform is used for the analysis of discrete time signal as well as discrete
time system.
Definition of z
Transform
z
transform of discrete time signal x(n) is given as S

z
transform pair

Types
of z transform: unilateral and bilateral
(i) Unilateral (or) one sided z
transform.

Here the summation exist in the range n = 0 to ∞.i.e. one sided.
(ii) Bilateral z transform:
It has both sided summation.

Here
the summation exist in between n = -∞ to ∞. i.e. both sided
Region of Convergence
(ROC)
ROC
is the region where z transform converges. z transform is an infinite power
series. This series is not convergent for all values of z.
Significance of ROC
(i)
ROC gives an idea about the values of z for which z transform can be
calculated.
(ii)
ROC is used to determine causality of the system
(iii)
ROC is used to determine stability of the system.
Properties of ROC
Property 1:
ROC
for a finite duration sequence includes entire z plane except at z = 0, and |z|
= ∞.
Proof:
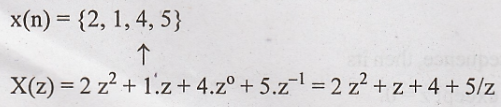
Here
x(z) = ∞ for z = 0 and ∞. Hence proved
Property 2:
ROC
does not contain any poles
Proof:
The
z transform of a" u(n) is calculated as

This
function has pole at z = a. But ROC is |z| > |a|
Hence
poles does not lie in ROC
Property 3:
ROC
is the ring in the z plane centered about origin.

Here
|z| is always a circular region centered around origin.
Property 4:
ROC
of causal sequence (right hand sided sequence) is in the form z > r
Proof:
Consider
right hand sided sequence an u(n).
It's
ROC is |z| > |a|, thus the ROC of right hand sequence is in the form of
|z|> r. Here 'r" is radius of circle.
Property 5:
ROC
of left sided sequence is in the form |z| < r.
Proof:
Consider
left sided sequence -an u(-n-1). Its ROC is |z| < |a|.
Thus
the ROC of left sided sequence is inside the circle of radius "r".
Property 6:
ROC
of two sided sequence is the concentric ring in z plane.
Property 7:
If
x(n) is finite causal sequence, then its
ROC
is entire z Plane except z = 0.
Proof:
Consider
the causal sequence, x(n) = {1,2,3},
Then
its z transform will be  . This sequence converges in entire z plane.
. This sequence converges in entire z plane.
Property 8:
ROC
of stable LTI system contains unit circle in the z plane.
Property 9:
The
ROC is a connected region.
Proof:
Convergence
of the sequence exists over certain area rather than discrete points. Hence ROC
is a connected region.
Properties of z Transform
Linearity
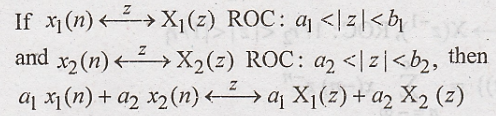
Proof:
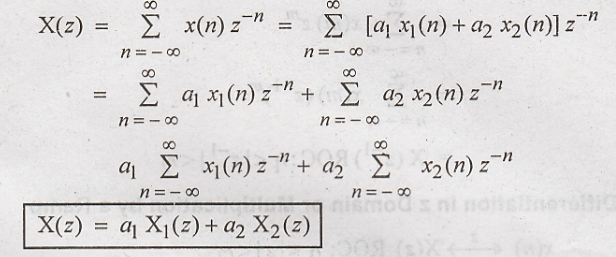
Time Shifting or
Translation
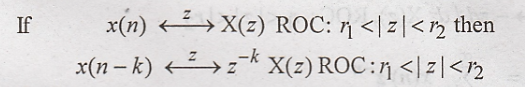
Proof:

Scaling in z Domain
(or) Multiplication by Exponential
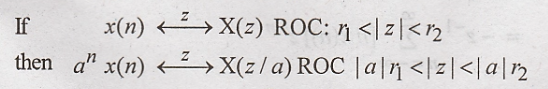
Proof:

Time Reversal

Proof:

Differentiation in z
Domain or Multiplication by a Ramp
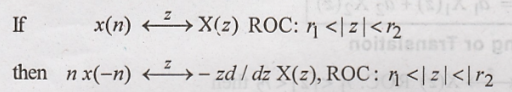
Proof:

Convolution in Time
Domain
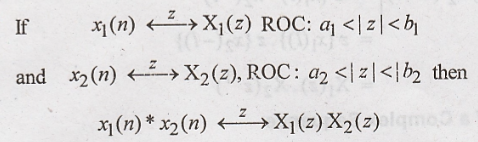
Proof:

By
interchanging order of summation
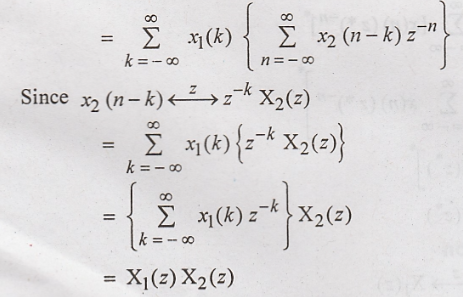
Correlation of Two
Sequences

Proof:
Correlation
of two sequence is given as


Conjugation of a
Complex Sequence
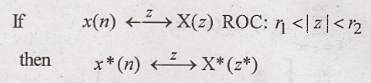
Proof:

Parseval's Relation

Proof:
Inverse
z transform of X1(z) is
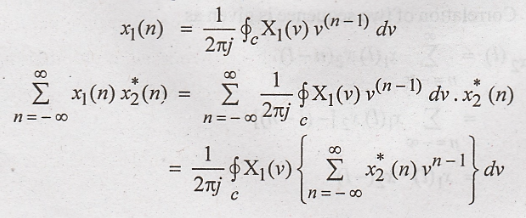

Initial Value Theorem

Proof:
z
transform of causal sequence
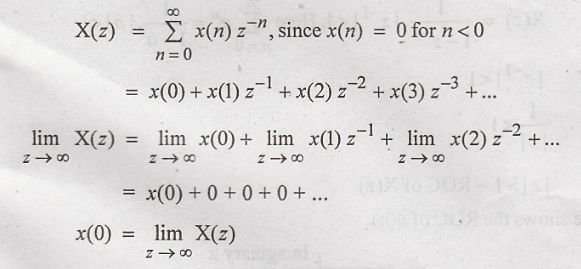
Signals and Systems: Unit IV: Analysis of Discrete Time Signals,, : Tag: : Properties of z transform - Z Transform
Related Topics
Related Subjects
Signals and Systems
EC3354 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
