Vectors x and y in V are orthogonal(perpendicular)

(e) Vectors x and y in V are orthogonal (perpendicular)

Definition 1:

Let V be an inner product space. Vectors x and y in V are orthogonal  (perpendicular) if <x,y> = 0

Definition 2:

A subset S of V is orthogonal if any two distinct vectors in S are orthogonal.

Definition 3:

A vector x in V is a unit vector if ||x|| = 1.

Definition 4:

A subset S of V is orthgonormal if S is orthogonal and consists entirely of unit vectors.

Note :

1. If S = {v₁, v₂, ...}, then S is orthonormal if and only if (v_i, v_j) = δ_ij, where δ_ij denotes the Kronecker delta.

2. Multiplying vectors by non-zero scalars does not affect their orthogonality and that if x is any non-zero vector, then (1/||x||)x is a unit vector.

The process of multiplying a non-zero vector by the reciprocal of its length is called normalizing.

Example

If F³, {(1, 1, 0), (1, −1, 1), (−1, 1, 2)} is an orthogonal set of non-zero vectors, but it is not orthonormal; however, if we normalize the vectors in the set, we obtain the orthonormal set

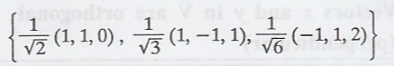
Example

Recall the inner product space H. We introduce an important orthonormal subset S of H.

i is the imaginary number such that i² = -1.

For any integer n, let f_n(t) = e^{i n t}, where 0 ≤ t ≤ 2л.

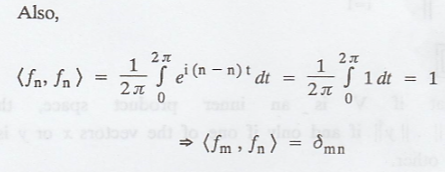
Problem 1.

Solution :

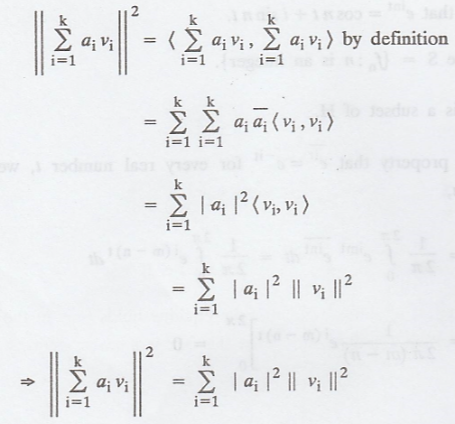
Problem 2.

Prove that if V is an inner product space, then |<x,y>| = ||x|| . ||y|| if and only if one of the vectors x or y is a multiple of the other.

Solution :

Let V be an inner product space.

To prove |<x,y>| = ||x|| . ||y|| if and only if one of the vectors x or y is a multiple of the other.

The result is trivial if y = 0, as y is a scalar multiple of x and there is the equality.

Now, assume that y ≠ 0, and then for a Є R

The above expression is equivalent to <x,y> ≤ ||x|| . ||y||

Observe that in the above inequality the equality holds only in the case that || x - ay || = 0 and hence, x = ay that is x is a scalar multiple of y.

Problem 3.

If V is an inner product space then derive ||x + y|| = ||x|| + ||y|| and generalise if to the case of n vectors.

Solution :

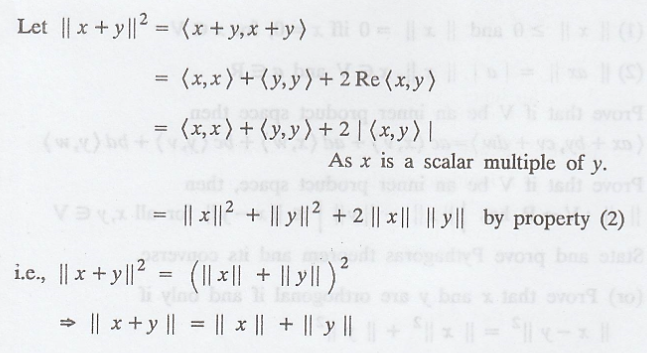
Again, generalize the above result to the case of n vectors.

EXERCISE 5.3

1. Prove that if V be an inner product space, the norm function 

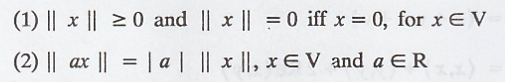
2. Prove that if V be an inner product space then

3. Prove that if V be an inner product space, then 

4. State and prove Pythagoras theorem and its converse.

(or) Prove that x and y are orthogonal if and only if ||x − y||² = ||x||² + ||y||²

5. Prove that ||x|| = ||y|| if and only if 

6. 

7. Show that [u₁, u₂, u₃] is an orthogonal set

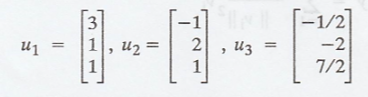
8. Prove that v / ||v|| is always a unit vector.

9. If the vectors u₁ = (1, 2i, i), u₂ = (0, 1 + i, 1), u₃ = (2, 1-i, i) Є C³, then find (i) ||u₁|| (ii) ||u₂|| (iii) ||u₃||