Random Process and Linear Algebra: Unit I: Probability and Random Variables,,
Uniform Distribution
Rectangular Distribution
A random variable X is said to have a continuous uniform distribution over an interval (a, b) if its probability density function is a constant = k, over the entire range of X. (i.e.,) f(x) = K, a < x
Uniform distribution
(or) Rectangular Distribution
i. Uniform Distribution
A random variable X is said to have a
continuous uniform distribution over an interval (a, b) if its probability
density function is a constant = k, over the entire range of X.
(i.e.,) f(x) = K, a < x <b
= 0, otherwise
Since, the total probability is always
unity.

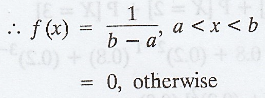
a and b are said to be the two
parameters of the uniform distribution on (a, b).
Note:
The uniform distribution is also known as rectangular ni distribution, since y
= f(x) describes a rectangle over the curve (the x-axis, between the ordinates
x = a and x = b.
ii. The distribution function of the uniform distribution
The distribution function F (x) is given
by

Since F(x) is not continuous at x = a
and x = b, it is not differentiable at these points.

everywhere except at x = a and x = b.
Note:
The pdf of a uniform variable 'X' in (-a, a) is given by

iii. Characteristic function of a uniform distribution
Characteristic function is given by
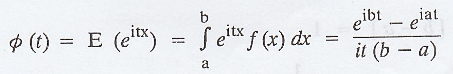
iv. Moments of a uniform distribution
Moments are given by

v. Mean deviation about the mean of uniform distribution
Mean distribution about mean is given by

Thus mean deviation of the uniform
distribution

Example 1.10.1
Electric trains on a certain line run
every half an hour between mid-night and six in the morning. What is the
probability that a man entering the station at a random time during this period
will have to wait atleast twenty minutes ? [A.U. A/M 2008]
Solution :
Let the random variable X denote the
waiting time in minutes for the next train.
Given that a man arrives at the station
at random
=> X is distributed uniformly on (0,
30) with density

Thus the probability that he has to wait
for atleast 20 minutes is

Example 1.10.2
If the random variable X follows uniform
distribution in (0, 1) with density f(x) = 1, 0 < x < 1 f(x) = 0,
otherwise find the density function of -2 log X.
Solution:
Let Y = -2 log X. Thus the distribution
function of Y is


Example 1.10.3
Show that for the uniform distribution :

the moment generating function about the
origin is  Also, moments of even order are given by
Also, moments of even order are given by 
Solution :
Moment generating function about origin
is given by
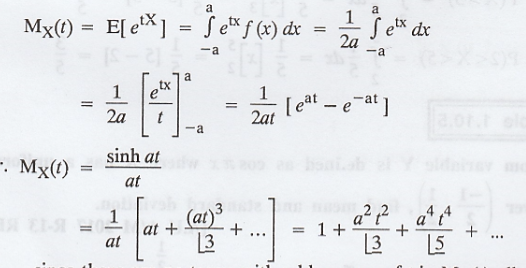
since there are no terms with odd powers
of t in Mx(t) all moments of odd order about origin vanish.


(i.e.,) all moments of odd order about
mean vanish. The moments of even order are given by
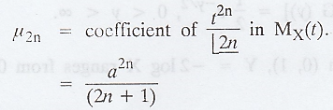
Example 1.10.4
If X is uniformly distributed over (0,
5), find the probability that (a) X < 2 (b) X > 3 (c) 2 < x < 5.
Solution:


Example 1.10.5
A random variable Y is defined as cos
πx
where X has a uniform p.d.f. over (-1/2, 1/2)
find mean and standard deviation. [A.U
A/M 2017 R-13 RP]
Solution:


Example 1.10.6
If X is uniformly distributed over (-a,
a), a > 0 find a, so as to satisfy the following: (a) P(X ≥ 1) = 1/3 (b) P(X
> 1) = 1/2
Solution:
X is uniformly distributed over (-a, a)

Example 1.10.7
X is uniformly distributed with mean 1
and variance 4/3, find P(X < 0). [A.U Tvli M/J 2010, CBT A/M 2011]
Solution:
Given that, mean = 1 => 
Variance = 4/3 => 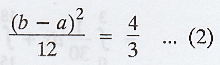
Solving equations (1) and (2) we get, b = 3 and a = -1
Therefore, f (x) = 1/b-a = 1/4
Hence, P(X < 0) = 
Example 1.10.8
Buses arrive at a specified bus stop at
15 minutes intervals starting at 7 a.m. that is 7 a.m., 7.15 a.m., 7.30 a.m.,
etc. If a passenger arrives at the bus stop at a random time which is uniformly
distributed between 7 and 7.30 a.m. find the probability that he waits (a) less
than 5 minutes (b) atleast 12 minutes for a bus.
Solution :
Let X denotes the time that a passenger
arrives between 7 and 7.30 a.m.
Then X ~ U(0, 30)
Then f(x) = 1/b-a = 1/30-0 = 1/30
(a) Passenger waits less than 5 minutes,
(i.e.,) he arrives between 7.10 - 7.15 or 7.25 - 7.30
P(Waiting time less than 5 minutes)
= P(10 ≤ x ≤ 15) + P(25 ≤ x ≤ 30)

(b) Passenger waits atleast 12 minutes,
(i.e.,) he arrives between 7 - 7.03 or 7.15 - 7.18.
P(Waiting time atleast 12 minutes)
= P(0 ≤ x ≤ 3) + P(15 ≤ x ≤ 18)
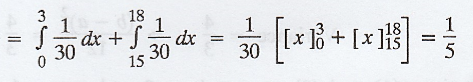
Example 1.10.9
A random variable 'X' has a uniform
distribution over (-3, 3) compute (i) P(X < 2), P(|X| < 2), P(|x-2| <
2), (ii) Find K for which P(X > K) = 1/3 [A.U M/J 2009, CBT A/M 2011]
Solution :
We know that the p.d.f. of a random
variable 'X' which is distributed uniformly in (-a, a) is
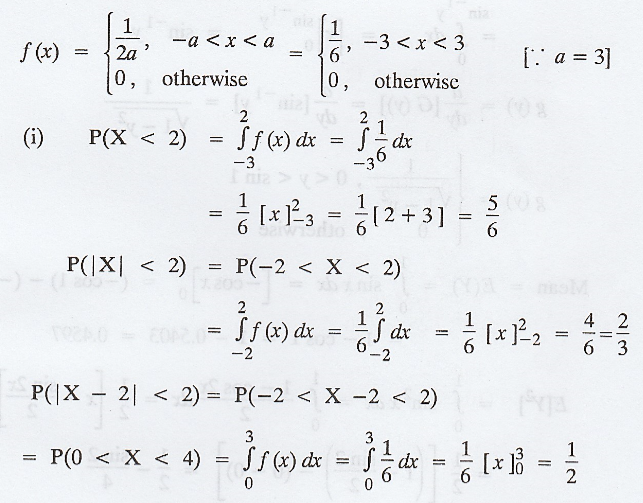
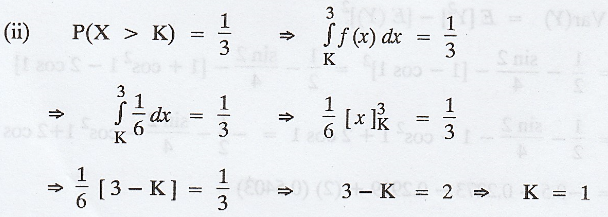
Example 1.10.10
If X is a random variable uniformly
distributed in (0, 1), find the pdf of Y = sin x. Also find the mean and
variance of Y. [A.U. M/J 2006]
Solution:
Given: Y = sin x
X has a uniform p.d.f over (0, 1)
g(y) = 1
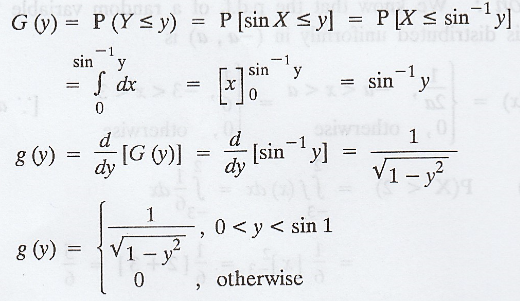

Example 1.10.11
X is uniformly distributed random
variable with mean 1 and variance 4/3. If 3 independent observations of X are
made, what is the probability that all of them are negative. [A.U A/M 2015 (RP)
R8]
Solution:
Let X ~ U (a, b)
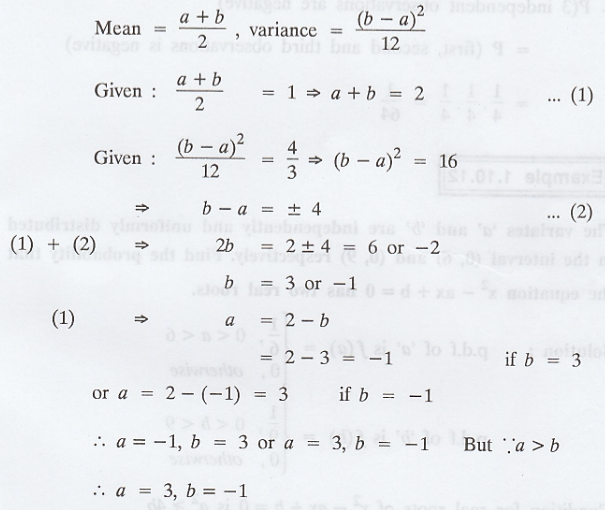
and the p.d.f of X, which is uniformly
distributed, is given by


.'. P(3 independent observations are
negative)
= P (first, second and third observations
is negative)

Example 1.10.12
The variates 'a' and 'b' are
independently and uniformly distributed
in the interval (0, 6) and (0, 9)
respectively. Find the probability that the equation x2 - ax + b = 0
has two real roots.
Solution :

Condition for real roots of x2
- ax + b = 0 is a2 ≥ 4b
i.e., the condition is b ≤ a2/4
.'. Required probability = 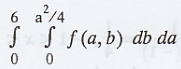
f(a, b) = f (a) f(b) = 1/54
The required probability

Example 1.10.13
Starting at 5.00 a.m. every half hour
there is a flight from San Francisco airport to Los Angeles International
Airport. Suppose that none of these planes is completely sold out and that they
always have room for passengers. A person who wants to fly to L.A. arrives at
the airport at a random time between 8.45 a.m and 9.45 a.m. Find the
probability that she waits (1) atmost 10 mins. (2) atleast 15 mins. [A.U M/J
2007]
Solution :
Let X be the uniform r.v. over the
interval (0, 60)



Example 1.10.14
Show that for the uniform distribution
f(x) = 1/2a -a < x < a the moment generating function about origin is sinh at/at [AU N/D 2006]
Solution:
Given : f(x) = 1/2a -a < x < a
To prove : MX(t) = sinh at/at
Proof : We know that the moment
generating function is
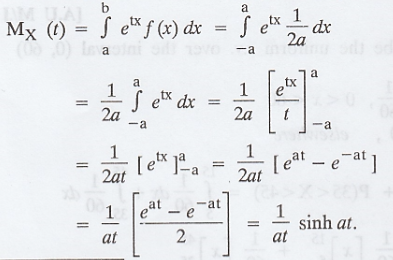
Example 1.10.15
If X is a random variable with a
continuous distribution function F(X), prove that Y= F(X) has a uniform
distribution in (0, 1). Further if
 find the range of Y
corresponding to the range of Y corresponding to the range 1.1 ≤ x ≤ 2.9 [A.U
N/D 2010]
find the range of Y
corresponding to the range of Y corresponding to the range 1.1 ≤ x ≤ 2.9 [A.U
N/D 2010]
Solution :
The distribution function of Y
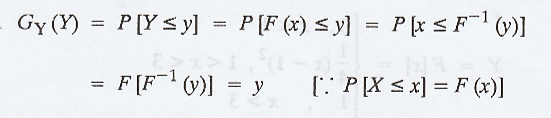
.'. the density function of Y is given
by

.'. Y follows uniform distribution in
(0, 1)
Given
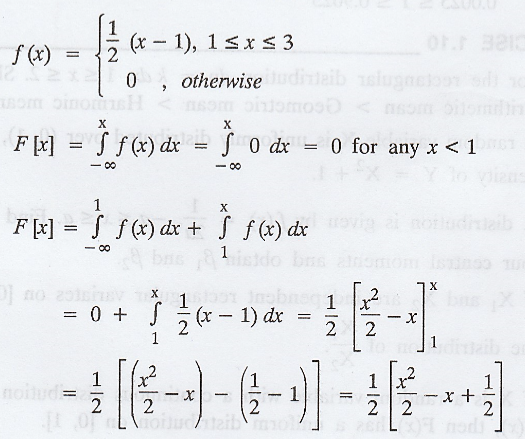

Random Process and Linear Algebra: Unit I: Probability and Random Variables,, : Tag: : Rectangular Distribution - Uniform Distribution
Related Topics
Related Subjects
Random Process and Linear Algebra
MA3355 - M3 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
