Transformation of Random Variables

TRANSFORMATION OF RANDOM VARIABLES

i. Two functions of two random variables

If (X, Y) is a two dimensional random variable with joint p.d.f. f_XY (x, y) and if Z = g(X, Y) and W = h (X, Y) are two other random variables then the joint p.d.f of (Z, W) is given by,

Note: This result holds good, only if the equation Z = g (X, Y) and W = h (X, Y) when solved, give unique values of x and y in terms of z and w.

ii. One function of two random variables

If a random variable Z is defined as Z = g(X, Y), where X and Y are given random variables with joint p.d.f f(x, y). To find the pdf of Z, we introduce a second Random variable W = h(X, Y) and obtain the joint p.d.f of (Z, W), by using the previous result. Let it be f_ZW (z, w). The required p.d.f of Z is then obtained as the marginal p.d.f is f_Z (z) is obtained by simply integrating f_ZW (Z, W) w.r. to w.

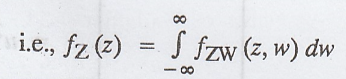
Example 2.4.1

Let (X, Y) be a two-dimensional non-negative continuous random variable having the joint density.

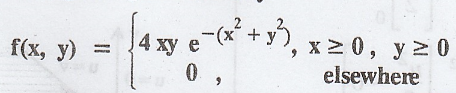 Find the density function of U = 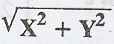[A.U A/M 2005] [A.U Tvli M/J 2010. Tvli A/M 2011] [A.U M/J 2016 R13 (RP)]

Solution :

The density function of U is

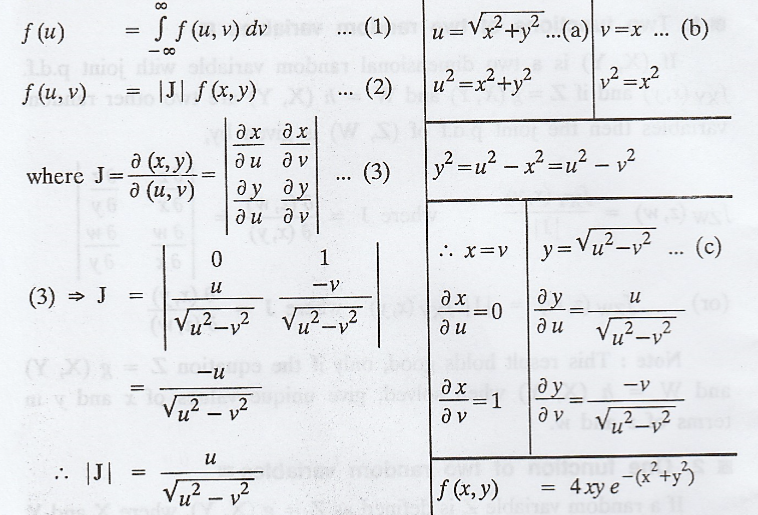
Example 2.4.2

If U = X + Y and V = X - Y, how are the joint p.d.f's of (X, Y) and (U, V) related?

Solution :

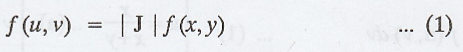
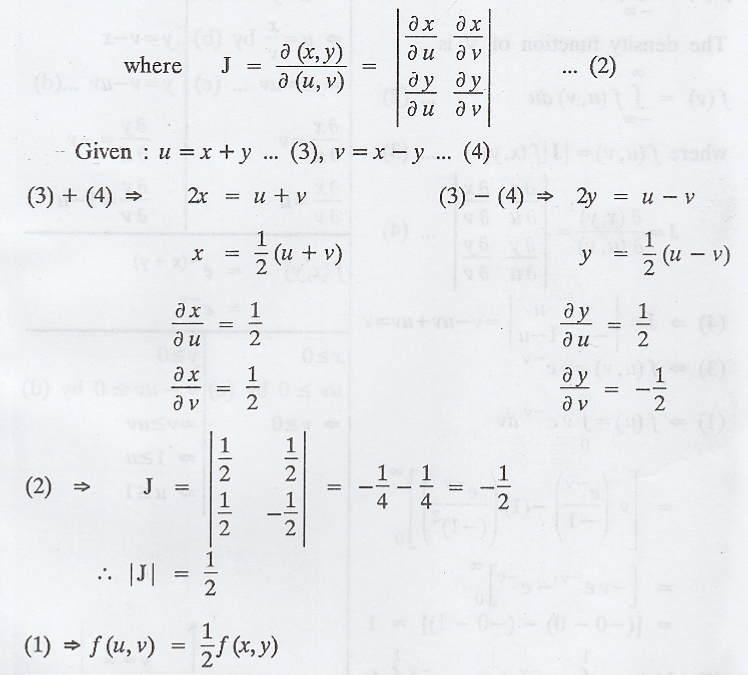
Example 2.4.3

If X and Y are independent random variables with p.d.f e^-x, x ≥ 0; e^-y, y ≥ 0 respectively. Find the density function of U = X / X+Y and V = X + Y. Are U & V independent ? [A.U. N/D 2006] [A.U Trichy M/J 2009, A.U N/D 2009, N/D 2011, N/D 2013] [A.U N/D 2015 R13, N/D 2017 (RP) R13, A/M 2017 (RP) R13] [A.U N/D 2018 R-17 PS]

Solution:

Since X and Y are independent,

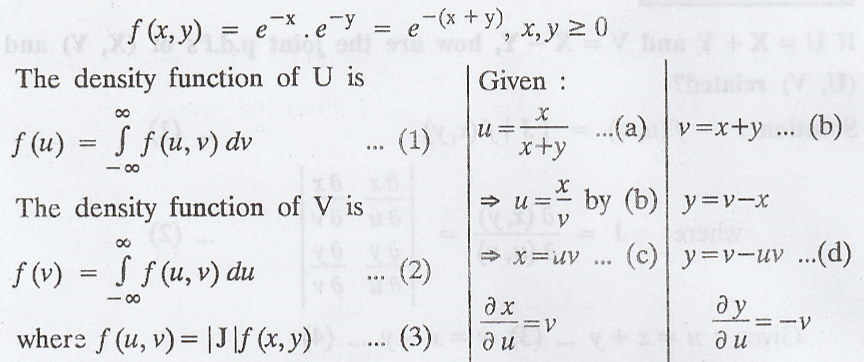
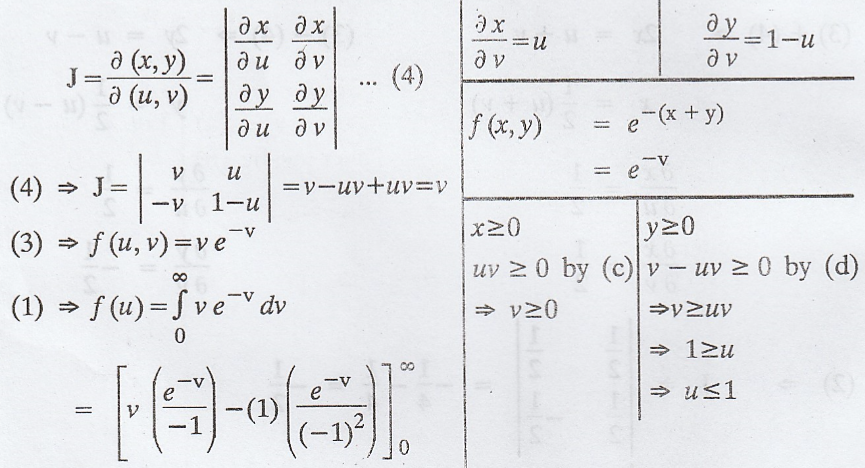
Example 2.4.4

If X and Y are independent random variables with density functions. f_X(x) = e^-x U(x) and f_Y(y) = 2e^-2y U(y). Find the density function of Z = X + Y [A.U. A/M 2005]

Solution :

X and Y are independent,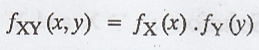 

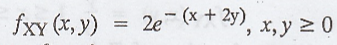
Here, U(x) and U(y) are unit step functions

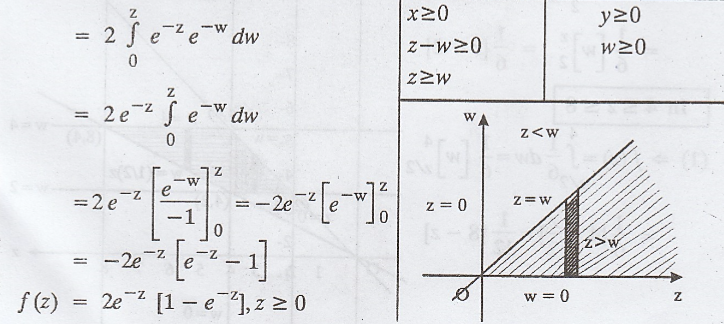
Example 2.4.5

If X and Y are independent random variables with density function f_X(x) = 1, in 1 ≤ x ≤ 2 and f_Y(y) = y/6, in 2 ≤ y ≤ 4, find the density function of Z = XY. [A.U A/M 2011]

Solution :

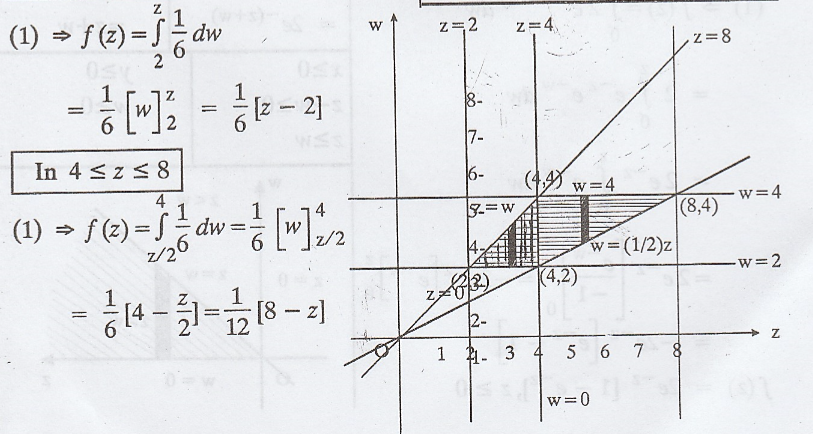
Example 2.4.6

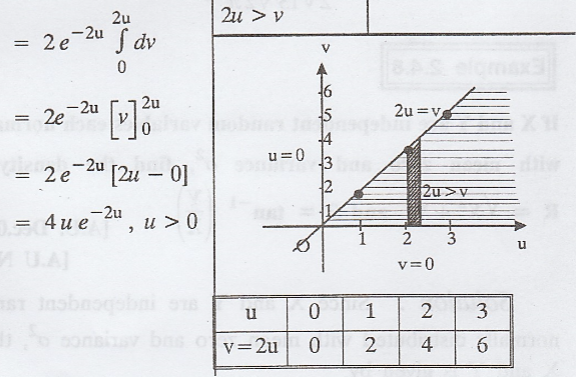
The joint p.d.f. of X and Y is given by f (x, y) = e^-(x+y) x > 0, y > 0, find the probability density function of U = X + Y / 2 [AU A/M 2003] [A.U. N/D 2006] [AU N/D 2009] [A.U CBT M/J 2010, CBT A/M 2011]

Solution:

The density function of U is

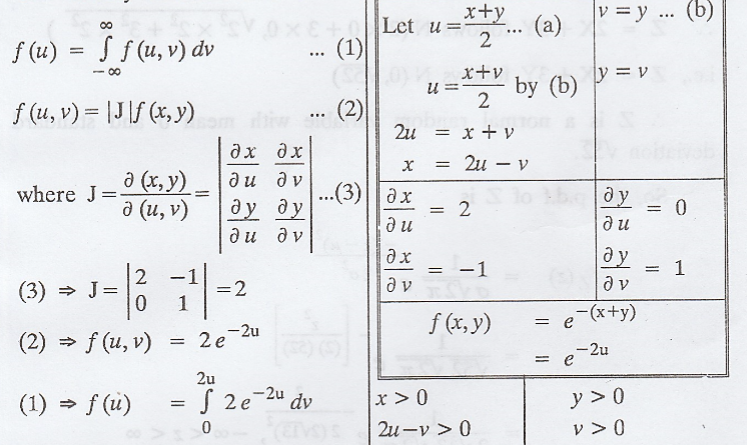
Example 2.4.7

If X and Y are independent random variables each following N (0, 2), find the probability density function of Z = 2X + 3Y. [AU A/M. 2003]

Solution :

Given:

X follows N(0, 2) and

Y follows N(0, 2)

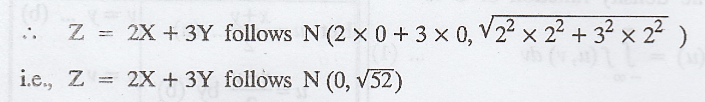
.'. Z is a normal random variable with mean 0 and standard deviation v52.

So, the p.d.f of Z is

Example 2.4.8

If X and Y are independent random variables each normally distributed with mean zero and variance σ², find the density functions of 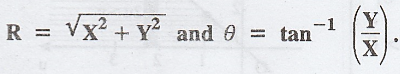[A.U. Dec.03, N/D 2013] [A.U N/D 2017 R-13]

Solution :

Since X and Y are independent random variables normally distributed with mean zero and variance σ², the joint pdf of X and Y is given by

Example 2.4.9

The random variables X and Y are statistically independent having a gamma distribution with parameters (m, 1/2) and (n, 1/2), respectively. Derive the probability density function of a random variable U = X / (X + Y). [AU N/D 2007, A.U N/D 2008]

Solution

Since X and Y are independent f (x, y) = f(x) f (y)

Example 2.4.10

If X and Y are independent exponential distributions with parameter 1, then find the p.d.f of U =X - Y. [A.U. Model, M/J 2007, M/J 2013] [A.U N/D 2015 R13 RP, N/D 2016 R13 PQT] [A.U N/D 2015 R-8, A/M 2017 R-08] [A.U N/D 2018 R-13 RP]

Solution:

The p.d.f of X and Y are

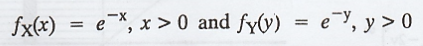
Since X and Y are independent, the joint p.d.f is

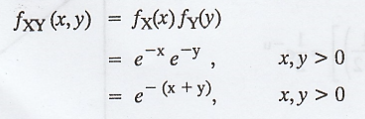
Example 2.4.11

If X and Y are independent random variables having density functions 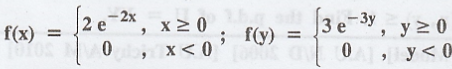 respectively, find the density functions of Z = X - Y. [A.U A/M 2011]

Solution:

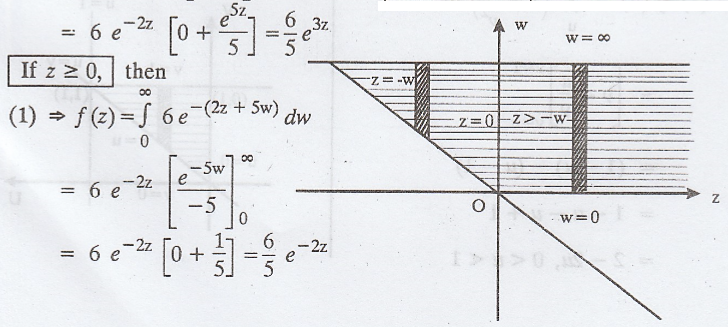
Example 2.4.12

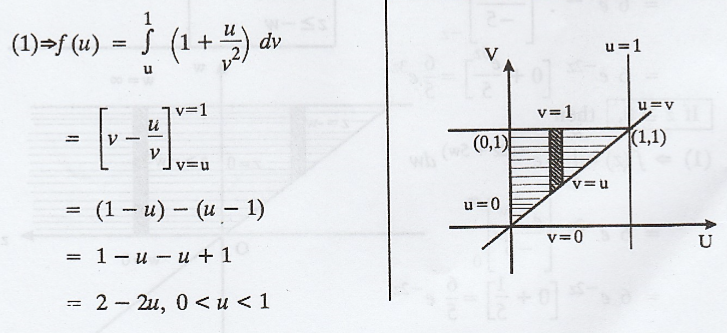
If the p.d.f of a two dimensional R.V (X, Y) is given by f(x, y) = x + y, 0 ≤ (x, y) ≤ 1. Find the p.d.f of U= XY. [A.U N/D 2018 R-13 PQT] [A.U Model] [A.U N/D 2006] [A.U Trichy A/M 2010] U [A.U Tvli N/D 2010, Trichy M/J 2011] [A.U M/J 2012] [A.U A/M 2015 (RP) R13, N/D 2017 (RP) R08] [A.U A/M 2018 R13]

Solution :

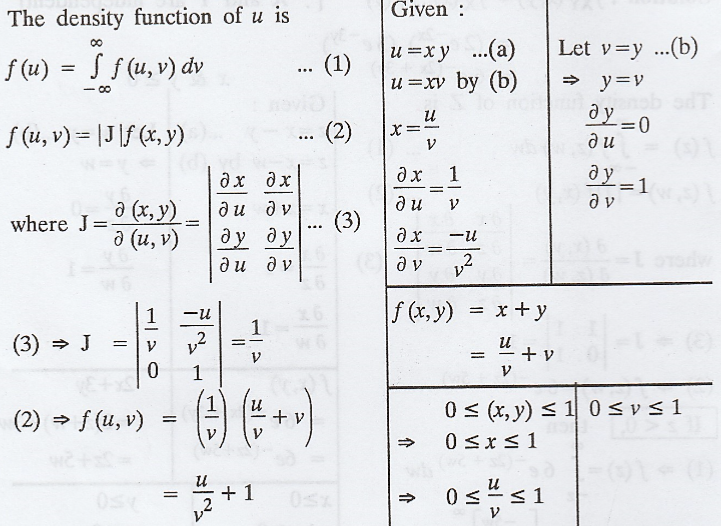
Example 2.14.13

If Z = g(X, Y) and W = h(X, Y), how are the joint p.d.f's of (X, Y) and (Z, W) related ?

Solution :

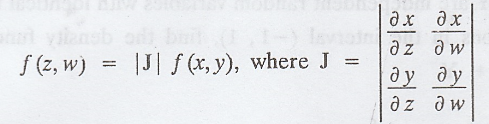
Example 2.4.14

If Z = 2X + 3Y and W = Y, how are the joint p.d.f's of (X, Y) and (Z, W) related?

Solution :

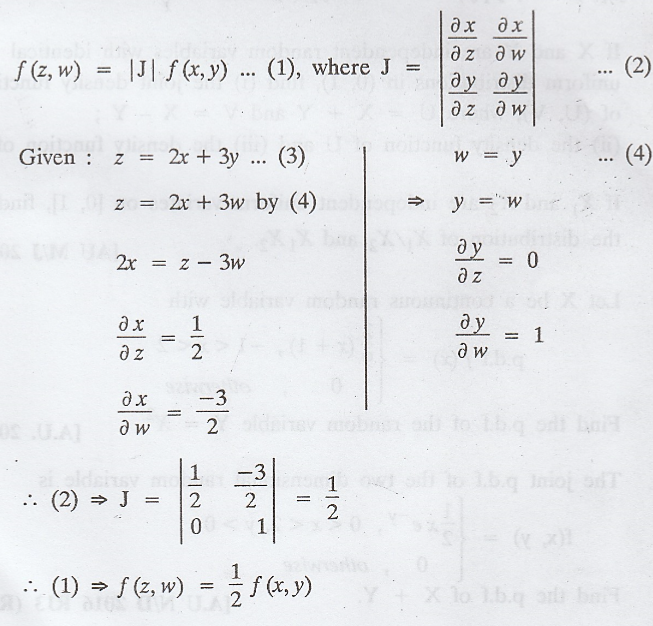
EXERCISE 2.4

1. Let f_x(x) = 2x, 0 ≤ x ≤ 1 and f_y(y) = y²/9, 0 ≤ y ≤ 3 be the p.d.f of the 2 independent random variables. Find the p.d.f of XY.

2. If X and Y are independent random variables with identical uniform distributions in the interval (-1, 1), find the density function of Z = X + Y.

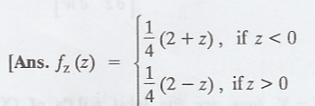
3. If X and Y are independent Random variables with f_X(x) = e^-x, f_Y(y) = 3e^-3y find f_Z(z), if Z = X/Y

4. If X and Y are independent random variables with identical uniform distributions in (0, 1), find (i) the joint density function of (U, V), where U = X + Y and V = X - Y; (ii) the density function of U and (iii) the density function of V.

5. If X₁ and X₂ are independent uniform variates on [0, 1], find the distribution of X₁/X₂ and X₁ X₂. [AU M/J 2006]

6. Let X be a continuous random variable with 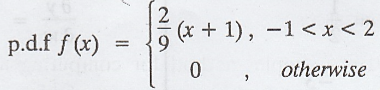 Find the p.d.f of the random variable Y = X² [A.U. 2006]

7. The joint p.d.f of the two dimensional random variable is 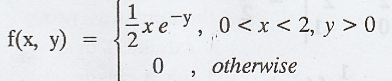 Find the p.d.f of X + Y. [A.U N/D 2016 R13 (RP)]

8. (i) Write down the formula to find the p.d.f of Z = XY in terms of p.d.f of X and Y if they are independent.

(ii) If U = X + Y and V = X - Y how are the joint p.d.f of (X, Y) and (U, V) related.

9. If the joint p.d.f of X₁ and X₂ is given by 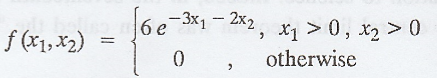 Find the probability density of U = X₁ + X₂