Random Process and Linear Algebra: Unit III: Random Processes,,
To find the Probability Distribution based on the Initial Distribution
Problems of Markov chain
Important problems of Markov Chain
Type 2. To
find the probability distribution based on the initial distribution
Example 3.7.9
If the initial state
probability distribution of a Markov Chain is 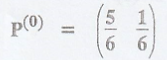 e and the tpm of the
chain is
e and the tpm of the
chain is 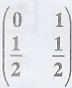 find the probability distribution of the chain after 2
steps. [A.U M/J 2012]
find the probability distribution of the chain after 2
steps. [A.U M/J 2012]
Solution:
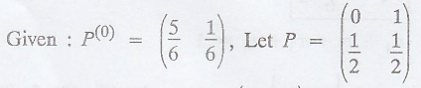
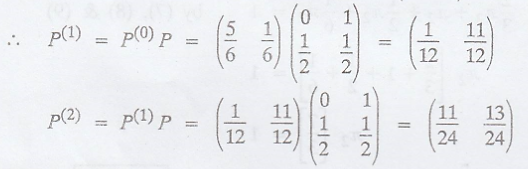
Example 3.7.10
The initial process of
the Markovian transition probability matrix is given by,  with
initial probabilities
with
initial probabilities 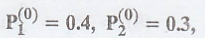
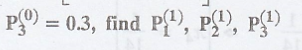
Solution:
Given: 

Example 3.7.11
Suppose, the
probability of a dry day (state 0) following a rainy day (state 1) is 1/3 and
that the probability of a rainy day following a dry day is 1/2. Given that May
1 is a dry day, find the probability that (a) May 3 is also a dry day and (b)
May 5 is also a dry day.
Solution
:
.'. The tpm of the
Markov Chain is
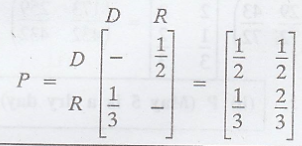

.'. The initial state
probability distribution is
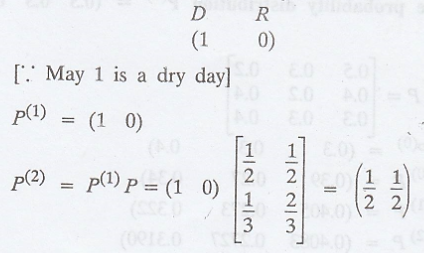
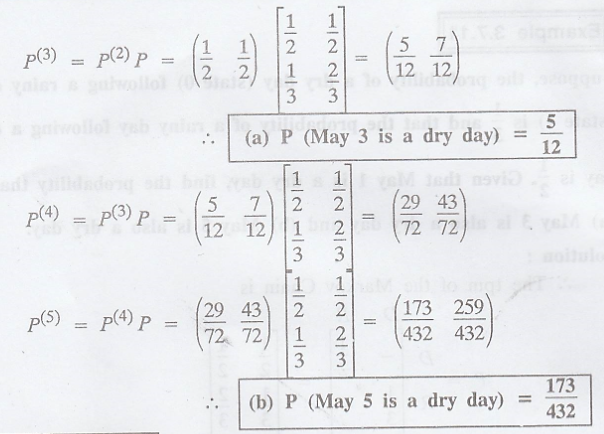
Example 3.7.12
A communication source
can generate 1 of 3 possible messages 1, 2 and 3. Assume that the generation
can be described by a homogeneous Markov Chain with the following tpm.
 and the initial state
probability distribution P(0) = (0.3 0.3 0.4) Find P(3)
and the initial state
probability distribution P(0) = (0.3 0.3 0.4) Find P(3)
Solution:
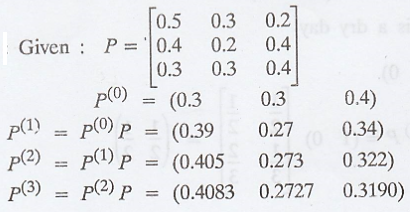
Example 3.7.13
A gambler has Rs. 2/-
he bets Re 1 at a time and wins Re 1 with probability 1/2. He stops playing if
he loses Rs. 2 or wins Rs. 4.
(a) What is the tpm of
the related Markov Chain?
(b) What is the
probability that he has lost his money at the end of 5 plays?
(c) What is the
probability that the game lasts more than 7 plays? [A.U M/J 2013, A/M 2014]
Solution
:
The state space of {Xn}
= {0, 1, 2, 3, 4, 5, 6}.
Since the game ends, if
the player loses all the money (Xn = 2 - 2 = 0) or wins Rs. 4 (Xn
= 2 + 4 = 6)
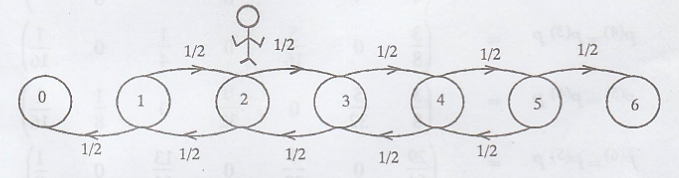
(a) The tpm of the
Markov Chain is

['.' If the tpm of a
chain is a stochastic matrix, then the sum of all elements of any row is equal
to 1]
The initial state
probability distribution of {Xn} is
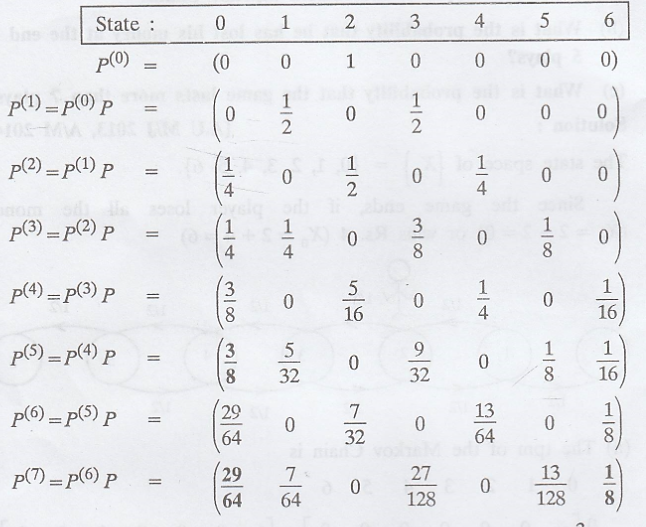
(b) P[the man has lost
all money at the end of 5 plays] 3/8
(c) P[the game lasts
more than 7 plays]
= P[the system is
neither in state 0 nor in state 6 at the end of the seventh round]
= 1- [P(X = 0) + P(X =
6)]
= 1 - [29/64 + 1/8]
= 1 - 37/64 = 27/64
Example 3.7.14
A raining process is
considered as two state Markov Chain. If it rains it is considered to be state
0 and if it does not rain, the chain is in state 1. The tpm of the Markov chain
is defined as 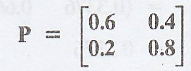
(i) Find the
probability that it will rain for 3 days from today assuming that it is raining
today.
(ii) Find also the
unconditional probability that it will rain after 3 ddays with the initial
probabilities of state 0 and state 1 as 0.4 and 0.6 respectively. [A.U N/D
2006, A.U N/D 2010]
Solution:
Given: 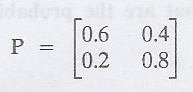
(i) If it rains today,
then the probability distribution for today is (1 0)


Example 3.7.15
A person owning a
scooter has the option to switch over to scooter, bike or car next time with
the probability of (0.3 0.5 0.2). If the tpm is  what are the
probabilities of the vehicles related to his fourth purchase?
what are the
probabilities of the vehicles related to his fourth purchase?
Solution:

Probabilities of his
fourth purchases = 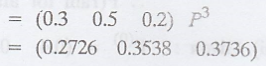
i.e., P [4th purchase
is a scooter] = 0.2726
P [4th purchase is a
bike] = 0.3538
P [4th purchase is a
car] = 0.3736
Type 3.
Problems based on Type 1 and Type 2.
Example 3.7.16
A man either drives a
car or catches a train to go to office each day. He never goes 2 days in a row
by train but if he drives one day, then the next day he is just as likely to
drive again as he is to travel by train. Now suppose that on the first day of
the week, the man tossed a fair die and drive to work if and only if a 6 appeared.
Find (a) The probability that he drives to work in the long run and (b) The
probability that he takes a train on the 3rd day. [A.U N/D 2015 R13 PQT] [A.U
N/D 2015 R13 RP] [A.U N/D 2017 (RP) R-13] [A.U N/D 2018 (RP) R-13]
Solution
:
Given:
Let π1 = the
man travels by train [T]
π2 = the man
travels by car [C]
.'. The tpm of the
Markov Chain is
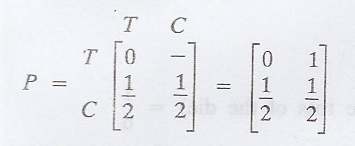

(a) Let π = (π1
π2) is the steady state distribution of the chain.
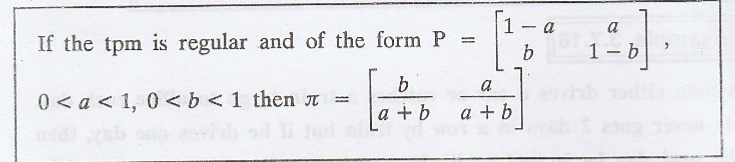
.'. P(the man travels
by car in the long run) = 2/3
(b) P(travelled by car)
= P(getting 6 in the
toss of the die) = 1/6
= P (travelling by
train) = 1 - 1/6 = 5/6
.'. The initial state
probability distribution is
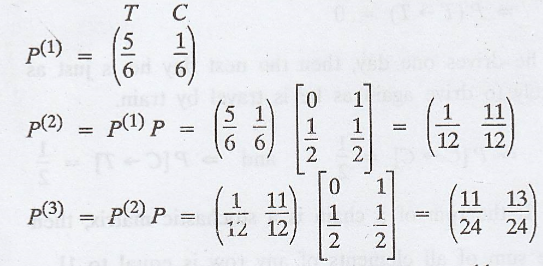
.'. P (the man travels
by train on the third day) = 11/24
Example 3.7.17
Assume that the weather
in a certain locality can be modeled as the homogeneous Markov Chain whose tpm
is given below.
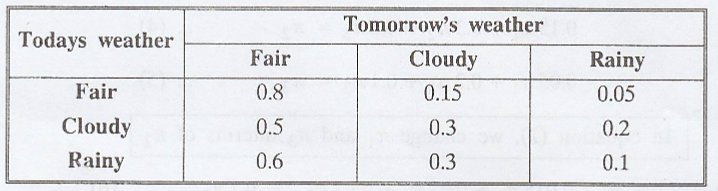
If the initial state
distribution is given by P(0) = (0.7 0.2 0.1), find P(2)
and 
Solution:
The tpm of the Markov
Chain is

(a) To find P(2)
Given : The Initial
state probability distribution is
P(0) = (0.7
0.2 0.1)
P(1) = P(0)
P = (0.7 0.2 0.1) P = (0.72 0.195 0.085)
P(2) = P(1)
P = (0.72 0.195 0.085) P = (0.7245 0.1920 0.0835)
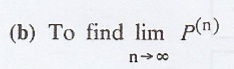
If π = (π1 π2
π3) is the steady state distribution of the chain, then by the
property of π, we have
πP = π ............(1)
π1 + π2 + π3 = 1
............(2)


.'. The steady state distribution of the chain is π = (π1 π2 π3)
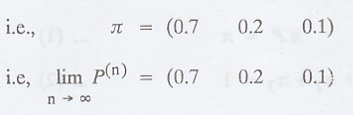
Example 3.7.18
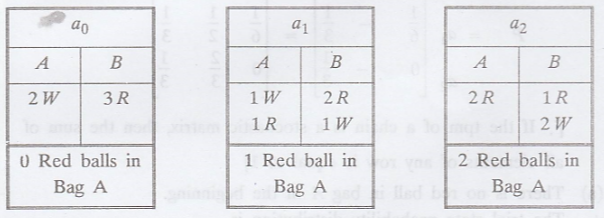
There are 2 white balls
in bag A and 3 red balls in bag B. At each step of the process, a ball is
selected from each bag and the 2 balls selected are interchanged. Let the state
'ai' of the system be the number of red balls in A after inter
changes.
(a) What is the
probability that there are 2 red balls in A after 3 steps?
(b) In the long run,
what is the probability that there are 2 red balls in bag A?[A.U N/D 2016 R-13]
Solution:
Here the state space of
the chain is
{Xn} = {a0,
a1, a2}
i.e., = {0, 1, 2}
Since the number of
balls in the bag A is always 2.
i.e., the number of red
balls in the bag A is 0, 1, 2.
Probability of changing
state
(i) From a0
to a0 = 0 ['.' 2R balls in A not possible]
(ii) From a0
to a2 = 0 ['.' 2R balls in A not possible]
(iii) From a2
to a0 = 0 ['.' 2R balls in A not possible]

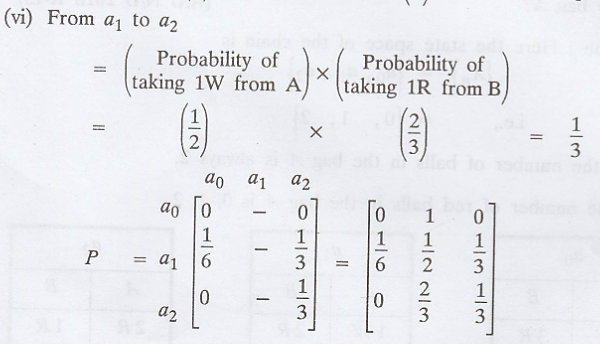
['.' If the tpm of a
chain is a stochastic matrix, then the sum of all elements of any row is equal
to 1]
(a) There is no red
ball in bag A in the beginning.
.'. The trial state
probability distribution is
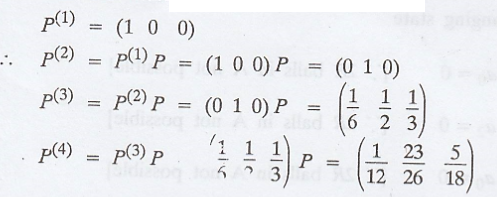
P(there is 2 red balls.
A after 3 steps) = 5/18
(b) If π = (π1
π2 π3) is the steady state distribution of the chain,
then by the property of π, we have
πP = π
................(1)
π1 + π2
+ π3 = 1 ................(2)
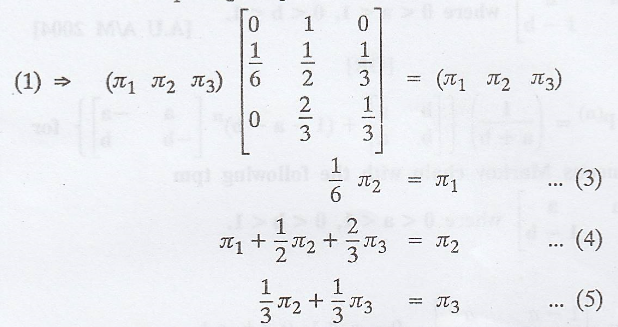
In equation (2), we
change, π1 and π3 interms of π2
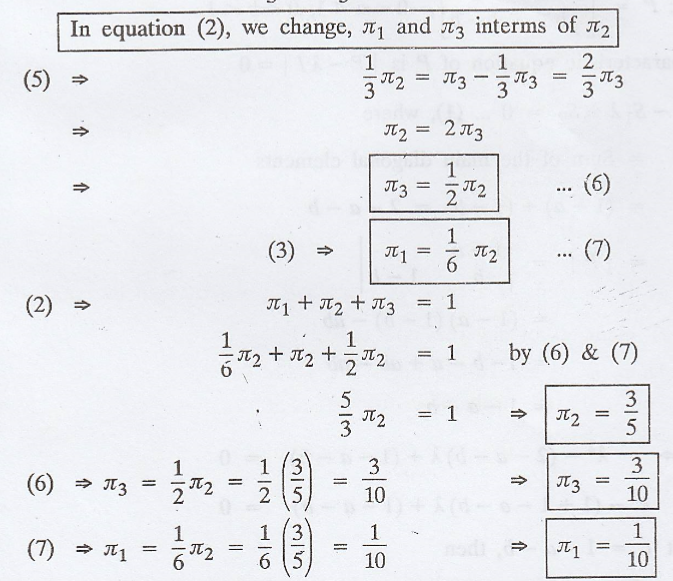
.'. The steady state
distribution of the chain is π = (π1 π2 π3)
i.e., π = (1/10 3/5
3/10) = (1/10 6/10 3/10)
Example 3.7.19
Find P(n)
for a homogeneous Markov Chain with the following tpm 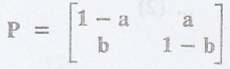 where 0 <
a < 1, 0 < b < 1. [A.U A/M 2004]
where 0 <
a < 1, 0 < b < 1. [A.U A/M 2004]
[OR]
Show that 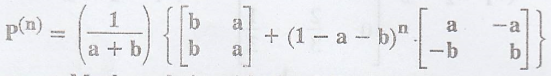 for the homogeneous Markov chain with the following tpm
for the homogeneous Markov chain with the following tpm
 where 0
< a < 1, 0 < b < 1.
where 0
< a < 1, 0 < b < 1.
Solution
:
Given:  0
< a <1, 0 < b < 1.
0
< a <1, 0 < b < 1.
The characteristic
equation of P is | P - λI | = 0
i.e., λ2 - S1λ
+ S2 = 0 ...... (1), where
S1 = Sum of
the main diagonal elements = (1 - a) + (1 - b) = 2 - a - b
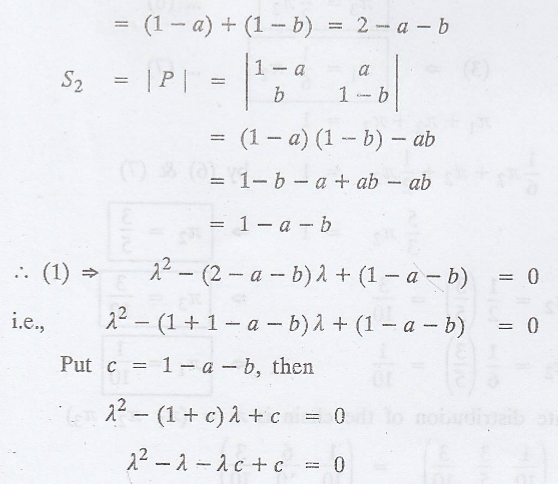
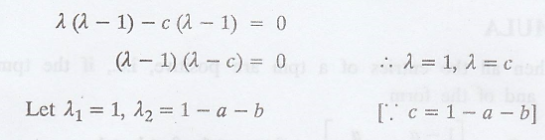
Thus, using the
SPECTRAL DECOMPOSITION METHOD
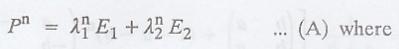
E1 and E2
are constituent matrices of P given by the expressions.
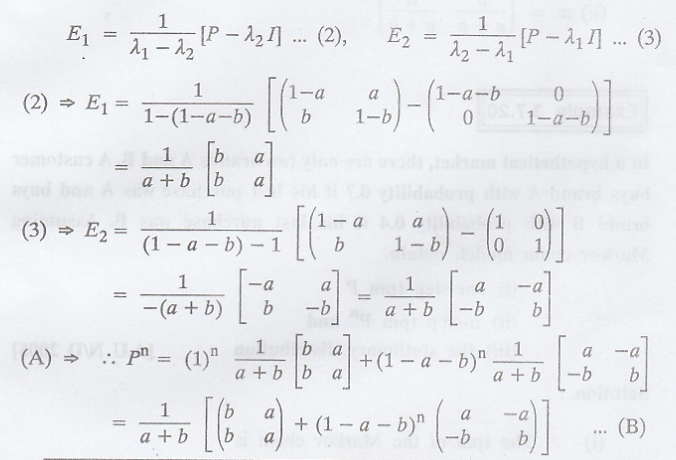

FORMULA
When all the entries of
a tpm are positive, i.e., if the tpm is regular and of the form
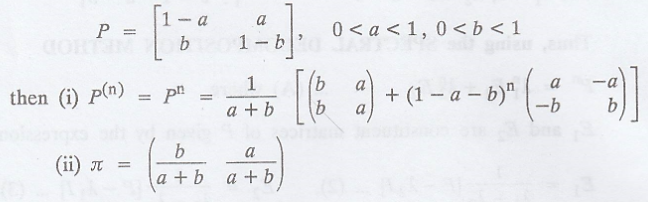
Example 3.7.20
In a hypothetical
market, there are only two brands A and B. A customer buys brand A with
probability 0.7 if his last purchase was A and buys brand B with probability
0.4 if his last purchase was B. Assuming Markov chain model, obtain.
(i) one-step tpm P
(ii) n-step tpm Pn
and
(iii) the stationary
distribution [A.U N/D 2005]
Solution
:
.'. The tpm of the
Markov chain is




Random Process and Linear Algebra: Unit III: Random Processes,, : Tag: : Problems of Markov chain - To find the Probability Distribution based on the Initial Distribution
Related Topics
Related Subjects
Random Process and Linear Algebra
MA3355 - M3 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
