Three Phase Power Measurement

THREE PHASE POWER MEASUREMENT

In ac circuits, power is measured with the help of wattmeter. A wattmeter is an instrument, which consists of two coils called the potential coil (PC) and the current coil (CC).

The potential coil having high resistance is connected across the load and carries the current proportional to the potential difference across the load. The current coil having low resistance is connected in series with the load.

The three phase power measurement can be carried out using the following methods:

i. One wattmeter method

ii. Two wattmeter methods

iii. Three wattmeter method.

One Wattmeter Method

In a balanced 3-wire, 3-phase load circuit the power in each phase is equal and, therefore, the total power of the circuit can be determined by multiplying the power measured in any one phase. Hence, the power measurement in three-phase, three-wire circuits can be carried out by using the one wattmeter only.

But this method has a disadvantage. Even a slight degree of unbalance in the loading produces a significant error in the measurement.

Two Wattmeter Method

Two Wattmeter Method can be employed to measure the power in a 3 phase, three- wire star or delta connected the balanced or unbalanced load.

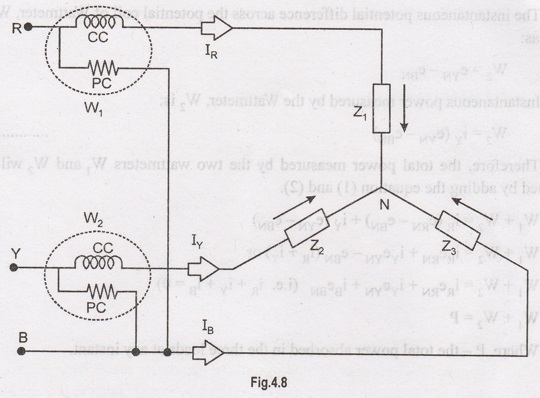
In two wattmeter method, the current coils of the wattmeter are connected with any two lines, say R and Y and the potential coil of each wattmeter is joined on the same line, the third line i.e. B as shown below in figure 4.8

The power measurement in three-phase, three-wire load circuits usually carried out using this method.

The current coils of two wattmeters are inserted in any two lines, and the potential coil is connected from its own current coil to the line without the current coil.

It can be proved that the sum of the power measured by two wattmeter W₁ and W₂ is equal to the total instantaneous power absorbed by the load. But in actual practice, wattmeters read the average power because of the inertia of their moving system.

The two wattmeter method of power measurement in three-phase circuits is suitable for every type of three-phase circuit weather circuit is balanced or unbalanced and star connected or delta connected.

1. Measurement of Power by Two Wattmeter Method in Star Connection

Considering the above figure (4.8) in which Two Wattmeter W, and W2 are connected, the instantaneous current through the current coil of Wattmeter, W, is given by the equation shown below:

W₁ = i_R

The instantaneous potential difference across the potential coil of Wattmeter, W₁ is given as:

W₁ = e_RN – e_BN

Instantaneous power measured by the Wattmeter, W₁ is

W₁ = i_R (e_RN – e_BN) ………………. (1)

The instantaneous current through the current coil of Wattmeter, W₂ is given by the equation:

W₂ = i_Y

The instantaneous potential difference across the potential coil of Wattmeter, W₂ is given as:

W₂ = e_YN – e_BN

Instantaneous power measured by the Wattmeter, W₂ is:

W₂ = i_Y (e_YN – e_BN) ………………. (2)

Therefore, the total power measured by the two wattmeters W₁ and W₂ will be obtained by adding the equation (1) and (2).

W₁ + W₂ = i_R (e_RN - e_BN) + i_Y (e_YN - e_BN)

W₁ + W₂ = i_R e_RN + i_Y e_YN - e_BN (i_R + i_Y) or

W₁ + W₂ = i_R e_RN + i_Y e_YN + i_B e_BN (i.e. i_R + i_Y +i_B = 0)

W₁ + W₂ = P

Where, P- the total power absorbed in the three loads at any instant.

2. Measurement of Power by Two Wattmeter Method in Delta Connection

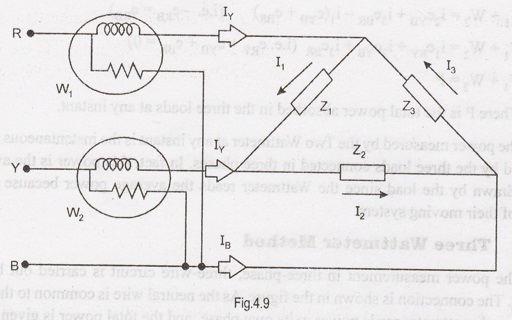
Considering the delta connected circuit shown in the figure 4.9

The instantaneous current through the coil of the wattmeter, W₁ is given by the equation:

W₁ = i_R = i₁ – i₃

Instantaneous power measured by the Wattmeter, W₁ will be:

W₁ = e_RB

Therefore, the instantaneous power measured by the wattmeter, W₁ will be given as:

W₁ = e_RB (i₁ – i₃) ………………. (3)

The instantaneous current through the coil of the wattmeter, W₂ is given by the equation:

W₂ = i_Y = i₂ – i₁

The instantaneous potential difference across the potential coil of wattmeter, W₂ :

W₂ = e_YB

Therefore, the instantaneous power measured by the wattmeter, W₂ will be :

W₂ = e_YB (i₂ – i₁) ………………. (3)

Hence, to obtain the total power measured by the two wattmeter the two equations, i.e. equation (3) and (4) has to be added.

W₁ + W₂ = e_RB (i₁ – i₃) + e_YB (i₂ – i₁)

W₁ + W₂ = i₁ e_RB + i₁ e_YB – i₃ e_RB – i₁ e_YB

W₁ + W₂ = i₂ e_YB + i₃ e_BR – i₁ (e_YB + e_BR) (i.e. –e_RB = e_RB )

W₁ + W₂ = i₁ e_RY + i₂ e_YB + i₃ e_BR (i.e. e_RY + e_YB + e_BR = 0)

W₁ + W₂ = P

Where, P- the total power absorbed in the three loads at any instant.

The power measured by the Two Wattmeter at any instant is the instantaneous power absorbed by the three loads connected in three phases. In fact, this power is the average power drawn by the load since the Wattmeter reads the average power because of the inertia of their moving system.

Three Wattmeter Method

The power measurement in three-phase, three-wire circuit is carried out by this method. The connection is shown in the figure. As the neutral wire is common to the three phases, each wattmeter reads power in its own phase, and the total power is given by the sum of the readings of three wattmeters.

Total power of load circuit, P_{3- φ} = W₁ + W₂ + W₃

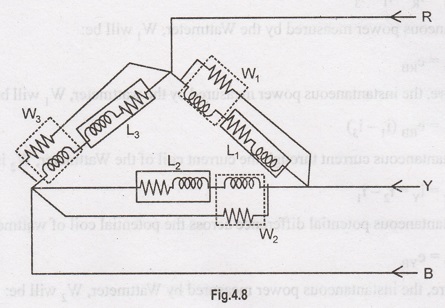
In the case of delta connected circuits, power measurement by three wattmeter method is very difficult because phase coils of load are required to be broken for inserting the current coils of wattmeter.

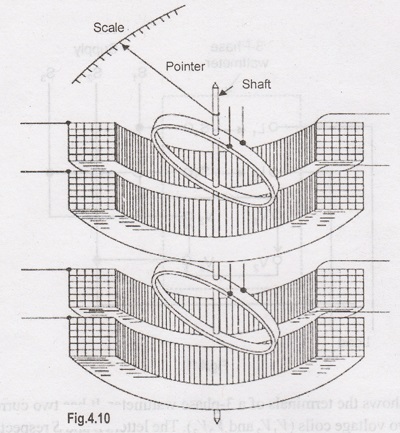
Three-phase Wattmeter

Two single phase wattmeters are required to measure the total power taken by a 3- phase circuit. Two such wattmeters may be combined into one so that total 3-phase power is read from a single scale. Such an arrangement gives rise to a 3-phase wattmeter. Fig. 4.11 shows a 3-phase dynamometer type wattmeter which is most commonly used in polyphase circuits. The arrangement consists of two similar dynamometer wattmeters; the two voltage coils being mounted on the same shaft and rotate in their respective current coils. The wattmeter elements are connected according to two-wattmeter method and the resulting deflection of the instrument pointer is a function of the algebraic summation of the torques produced by the individual element. The deflection of the instrument pointer is therefore a function of the total power.

In the design of such a 3-phase wattmeter, care must be taken that the two elements have no mutual action i.e., field from one element must not produce torque in the other. This may be checked by exciting the current circuit of one element and the voltage circuit of the other. There should be no deflection for this connection. Also the two elements must be matched in characteristics. This may be checked by connecting the elements with voltage circuits in parallel and the current circuits in series opposing. Again there should be no deflection.

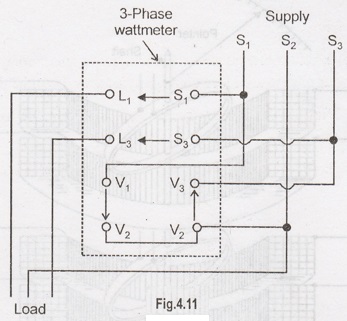
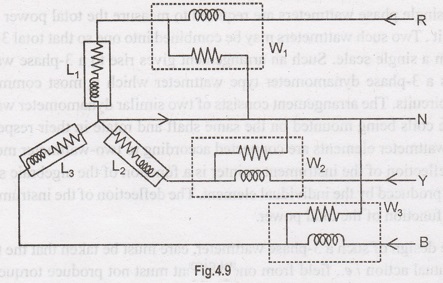
Fig. 4.11 shows the terminals of a 3-phase wattmeter. It has two current coils (L₁ S₁ and L₃ S₃) and two voltage coils (V₁ V₂ and V₂ V₃). The letters L and S respectively stand for load and supply.

Note that current coils and voltage coils are connected in the two supply lines (S₁ and S₃ in the present case) of the 3-phase circuit. Observing polarity is essential in a 3- phase wattmeter because if the instrument is not connected correctly, it may indicate upscale but incorrectly.

A convenient rule to follow is to connect the instrument so that, as the current flows from the supply, it enters both the current and voltage circuits of the wattmeter at the marked (0 or ±) terminals. Note the arrowheads in the diagram. The arrowhead between S₁ and L₁ indicates that positive direction of current is from S₁ to L₁. Similarly positive direction of voltage is from V₁ to V₂ and from V₂ to V₃.