Random Process and Linear Algebra: Unit V: Linear Transformation and Inner Product Spaces,,
The Matrix Representation of a Linear Transformationn
Definitions and Problems on The matrix representation of a Linear transformation
THE MATRIX REPRESENTATION OF A LINEAR TRANSFORMATION
Definition: Ordered Basis :
Let V be a finite-dimensional vector space. An
ordered basis for V is a basis for V endowed with a specific order; that is, an
ordered basis for V is a finite sequence of linearly independent vectors in V
that generates V.
Example
If F3, α = {e1, e2,
e3} can be considered an ordered basis. Also {e2, e1,
e3} is an ordered basis, but α ≠ β as ordered bases.
Note: For the vector space Fn, we call (e1,
e2, ..., en} the standard ordered basis for Fn.
Similarly, for the vector space Pn(F), we
call {1, x, ..., xn} the standard ordered basis for Pn(F)
Definition :
Let 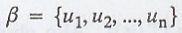 be an ordered basis for a
finite-dimensional vector space V. For
be an ordered basis for a
finite-dimensional vector space V. For  be the unique scalars such
that
be the unique scalars such
that

We define the coordinate vector of x relative to β,
denoted [x]β by
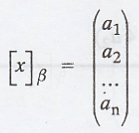
Example

Note :
The promised matrix representation of a linear
transformation. Suppose that V and W are finite-dimensional vector spaces with
ordered bases  respectively. Let T : V → W be linear. Then for
each j, 1 ≤ j ≤ n, there exist unique scalars
respectively. Let T : V → W be linear. Then for
each j, 1 ≤ j ≤ n, there exist unique scalars 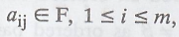 such that
such that
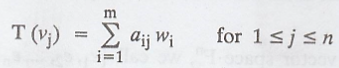
Definition :
Using the notation above, we call the m x n matrix A
defined by Aij = aij the matrix representation of T in
the ordered basis β and  then we write
then we write 
Note: The jth
column of A is simply  Also observe that If U : V → W is a linear
transformation such that
Also observe that If U : V → W is a linear
transformation such that 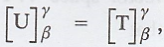 then U = T
then U = T
Example 1.

Note: Plural of basis
is bases

Example 2



Problem 1

Solution :

Similarly, for another basis,
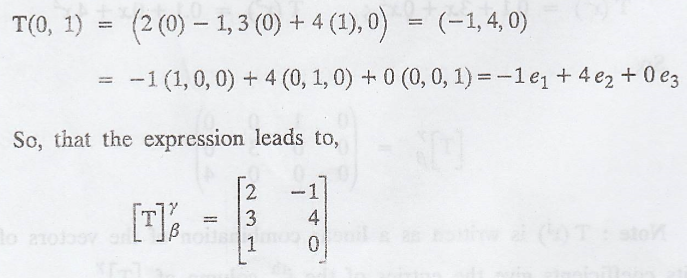
Problem 2

Solution :

Similarly, for another two basis.

Problem 3

Solution :

Problem 4

Solution :

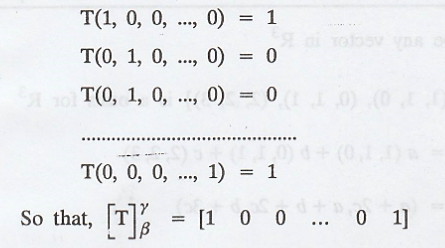
Problem 5

Solution :

First fine the images of the basis vectors
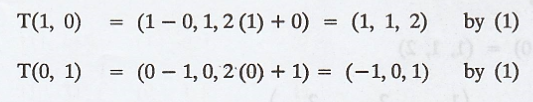
Write these images as a linear combination of the
basis vectors in γ
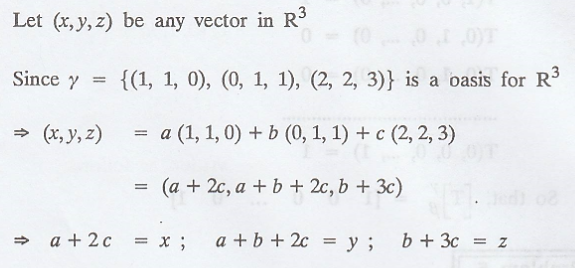
Solve we get
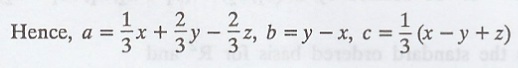
Hence, the vector (x,y,z) can be written as a linear
combination of the basis vectors in
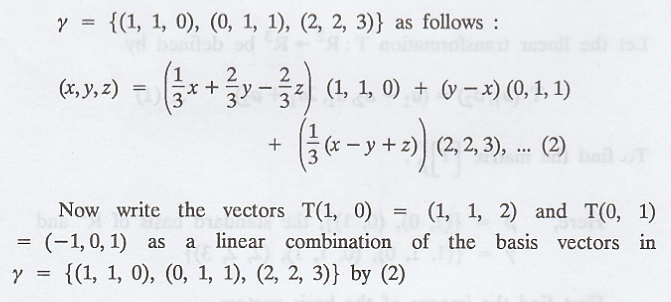
Thus,


The vector T(0,1) = (-1,0,1) can be written as
follows:

Hence, the matrix of the linear transformation with
respect to the bases β ans γ is

Problem 6


Solution :

Problem 7
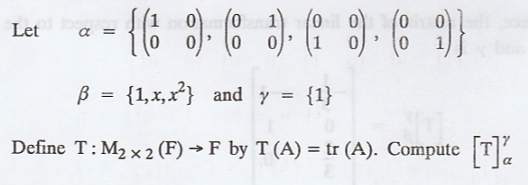
Solution :
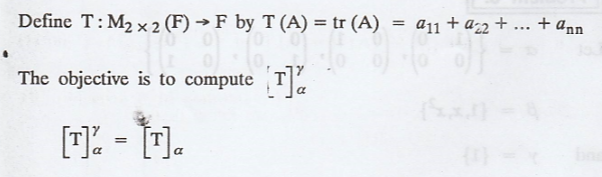

(b) T : V → Fn, T : V → V
Problem 1
Let V be an n-dimensional vector space with an
ordered basis β. Define T : V → Fn by T(x) = [x]β. Prove
that T is linear.
Solution :
Given that V is an n dimensional vector space over
the field F and β = {v1, ..., vn} is its basis.
So, every vector in V can be written as a linear
combination of β = {v1, ..., vn}
On the other hand, T : V → Fn is a
function such that T(x) = [x]β
Note that [x]β is the column of the
coefficients of the linear combination that x is written using β = {v1,
... vn}
Now, by the properties of matrices, we know that

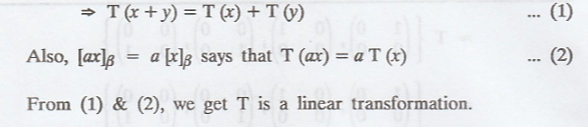
Problem 2

Solution :
A complex number z = a + ib can be written as (a, b)
But both a and b are real numbers.
.'. the set of complex numbers C can be followed as
R2
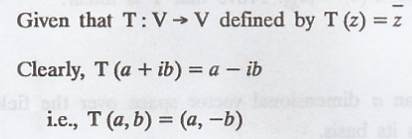
To prove T is linear,
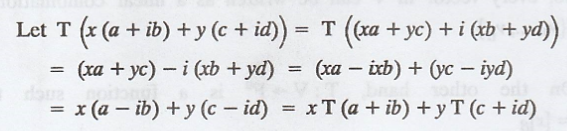
.'. T is a linear transformation.
Given basis is {1, i}
i.e., {1+Oi, 0+ li} or {(1, 0), (0, 1)}
(i) We write the images of the basis under T.

(ii) We write the images as the linear combinations
of the co-domain basis.
While the co-domain is also C, we get

(iii) We write the coefficients of the linear combinations as the columns of the matrix.

(c) T, U : V → W, T : V → W
Definition :
Let T, U : V → W be arbitrary functions, where V and
W are vector spaces over F, and let a Є F.

THEOREM 1.
Let V and W be vector spaces over a field F, and let
T, U : V → W be linear.
(a) For all a Є F, a T + U is linear.
(b) Using the operations of addition and scalar
multiplication in the preceding definition, the collection of all linear
transformations from V to W is a vector space over F.
Proof :

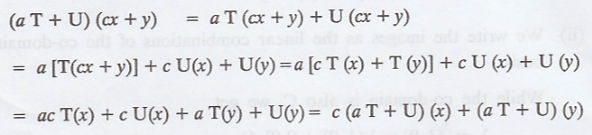
So aT + U is linear.
(b) Let V and W be two vector spaces over F : T, U :
V → W be linear transformation.
Use the operations of addition and scalar
multiplication to prove that the collection of all linear transformation of
this type from V to W is a vector space over F.
Suppose a Є F, then, define T + U : V → W by,
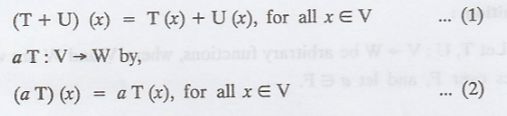
Clearly, the transformation T + U is linear.
Assume S is the set of all linear transformation as
defined above.
For each pair of transformations T, U in S there is
a unique transformation T+U in S defined by (T+U)(x) = T(x) + U(x)
Also, for all a F and each transformation T in S
there is a unique transformation a T in S
i.e., defined by (a T)(x) = a T(x)
(i) Commulativity of addition: To prove that for all T, U Є S. T + U = U + T.
Take T + U, which is defined as,

(ii)
Associativity of addition: Prove that for all T, U, P Є S.
i.e., To prove (T + U) + P = T + (U + P)
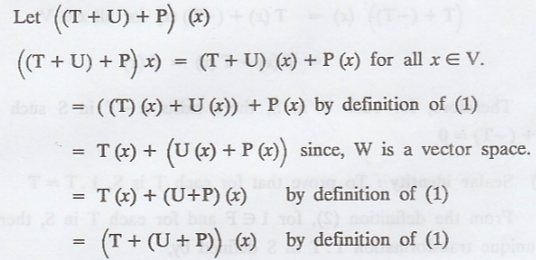
Therefore, for all T, U, P in S,
(T + U) + P = T + (U + P)
(iii) Additive Identity: To prove that there exists a transformation in S, denoted by T0, that is defined as T0(x) = 0, such that T + T0 = T for each T in S.
Here, T0 acts as zero transformation and play the
role of zero vectors.
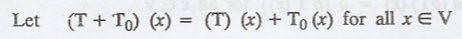
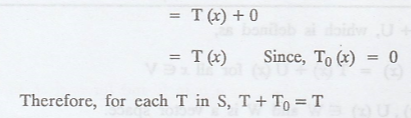
(iv)
Additive inverse: To prove that for each T in S, there
exists a -T in S such that T + (-T) = 0
From the definition (2), for -1 Є F and for each T
in S, there is a unique transformation -1. T in S defined by

Therefore, for each T in S, there exists a -T in S
such that T + (-T) = 0
(v)
Scalar identity: To prove that for each T is S, 1. T = T
From the definition (2), for 1 Є F and for each T in
S, there is a unique transformation 1. T in S defined by,
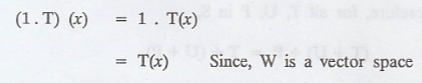
Therefore, for each T in S, 1.T = T
(vi)
Scalar Associativity: To prove that for each pair of elements
a, b in F, and for each T in S.
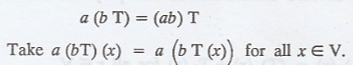
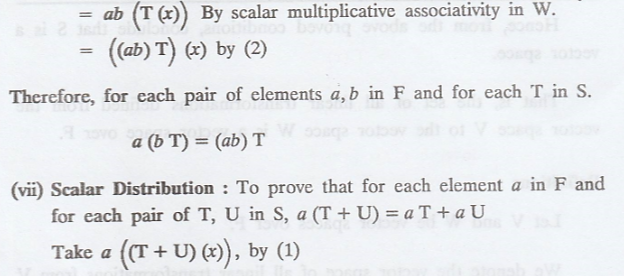


Hence, from the above proved conditions, conclude
that S is a vector space.
That is, the set of all linear transformations
defined from the vector space V to the vector space W is a vector space over F.
Definitions :
Let V and W be vector spaces over F.
We denote the vector space of all linear
transformations from V into W by L(V, W).
In the case that V = W, we write L(V) instead of
L(V, W).
THEOREM 2.
Let V and W be finite-dimensional vector spaces with
ordered bases β and γ, respectively, and let T, U : V → W be linear
transformations. Then

Proof :
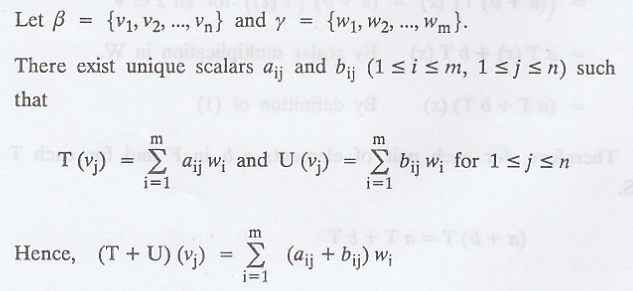
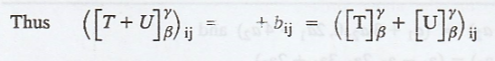
(b) If T : V → W is a line transformation, then the
matrix representation of T is obtained in the following manner.
(i) β = {v1, ..., vn} is the
basis of V and we find the images of β = {v1, ..., vn}
under T.
(ii) We write the images as the linear combinations
of γ = {w1, ..., wm}
(iii) We write the coefficients these linear combinations
as the columns of a matrix



Let β and γ be the standard ordered bases of R2
and R3, respectively. Then

If we compute T + U using the preceding definitions,
we obtain
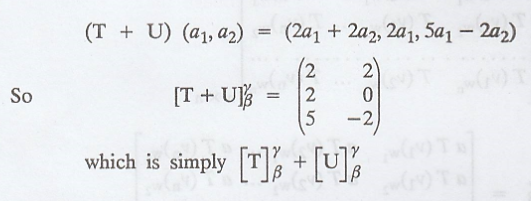
Problem 1
Let V and W be vector spaces, and let T and U be
non-zero linear transformations from V into W. If R(T) ∩ R(U) = {0}, prove that
{T, U} is a linearly independent subset of L(V, W).
Solution :
Let T and U be non-zero linear transformations from
V into the vector space W.
R(T) ∩ R(U) = {0}
To prove that T and U are linearly independent
We consider  is the zero transformation.
is the zero transformation.
Applying any vector x in V on both sides, we get (aT
+ b U) (x) = 0 (x)
By the definition of addition and scalar
multiplication of transformation, we get

So, the vectors ax and -bx have the same image under
T and U.
In other words, ax and -bx are the common range of T
and U.
But by hypothesis,
We have R(T) ∩ R(U) = {0}
=> ax = 0 and -bx = 0 for an arbitrary vector x
in V.
Consequently, there is the only possibility that a =
0 and b = 0
Thus, we have prove that (a T + b U) (x) = ![]() => a = 0 and b = 0
=> a = 0 and b = 0
Therefore, T and U are linearly independent.
Problem 2.
Let V and W be vector spaces, and let S be a subset
of V. Define S0 = {T Є L (V, W) : T(x) = 0 for all x Є S}. Prove the
following statement.
S0 is a subspace of L (V, W)
Solution :

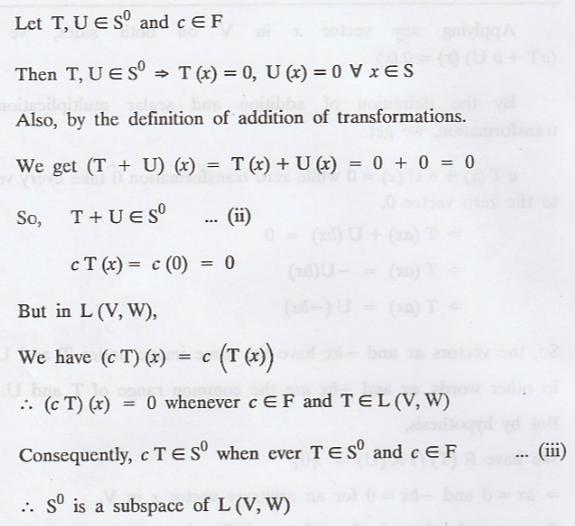
Problem 3
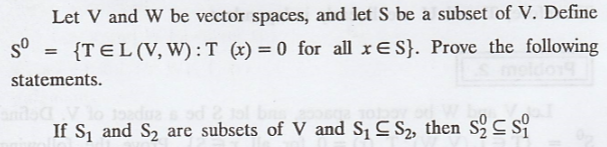
Solution :


EXERCISE 5.2
1. Label the following statements as true or false.
Assume that V and W are finite-dimensional vector spaces with ordered basis β
and γ, respectively, and T, U : V → W are linear transformations.
(i) For any scalar a, a T + U is a linear
transformation from V to W.
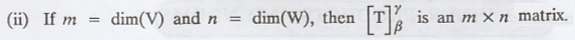
(iii) L(V, W) is a vector space.
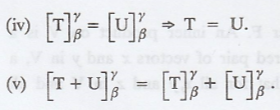
2. Let β and γ be the standard ordered bases for Rn
and Rm respectively. For each linear transformation T : Rn
→ Rm, compute 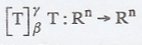 is defined by
is defined by 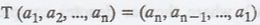
Random Process and Linear Algebra: Unit V: Linear Transformation and Inner Product Spaces,, : Tag: : - The Matrix Representation of a Linear Transformationn
Related Topics
Related Subjects
Random Process and Linear Algebra
MA3355 - M3 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
