Random Process and Linear Algebra: Unit V: Linear Transformation and Inner Product Spaces,,
The Gram-Schmidt Orthogonalization Process and Orthogonal Complements
Discuss about The Gram-Schmidt Orthogonalization Process and Orthogonal Complements and theorems
THE
GRAM-SCHMIDT ORTHOGONALIZATION PROCESS AND ORTHOGONAL COMPLEMENTS
Definition :
Let V be an inner
product space. A subset of V is an orthonormal basis for V if it is an ordered
basis that is orthonormal.
Example 1.
The standard ordered
basis for Fn is an orthonormal basis for Fn.
Example 2.
The set 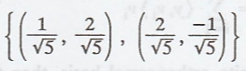 is
an orthonormal basis for R2
is
an orthonormal basis for R2
THEOREM 1.
Let V be an inner
product space and S = {v1, v2, ..., vk} be an
orthogonal subset of V consisting of non-zero vectors. If y Є span (S) then

Proof:
Let y Є L[S]

Using this in (1), we
get the required result.
Corollary
1.
If, in addition to the
hypotheses of Theorem 1, S is orthonormal and y Є span(S), then
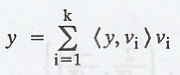
If V possesses a finite
orthonormal basis, then Corollary 1 allows us to compute the coefficients in a
linear combination very easily.
Corollary
2.
Let V be an inner
product space, and let S be an orthogonal subset of V consisting of non-zero
vectors. Then S is linearly independent.
Proof:
Suppose that v1,
v2, ..., vk Є S and
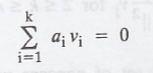
As in the Theorem 1
with y = 0, we have 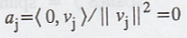 for all j. So S is linearly independent.
for all j. So S is linearly independent.
Example 3.
By corollary 2, the
orthonormal set is an orthonormal basis for R3
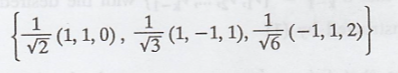
Let x = (2, 1, 3). The
coefficients given by Corollary 1 to Theorem 1 that express x as linear
combination of the basis vectors are

As a check, we have we
have

THEOREM 2.
Let V be an inner
product space and S = {w1, w2, ..., wn} be a
linearly independent subset of V. Define S' = {v1, v2,
..., vn} when v1 = w1 and

Then S' is an
orthogonal set of nonzero vectors such that span(S') = span(S)
Proof:
We prove this by
Mathematical induction.


which contradicts the
assumption that Sk is linearly independent.

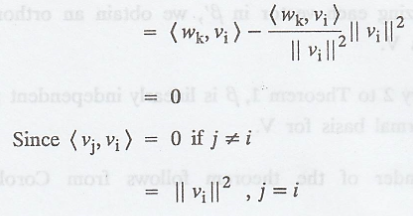
by the induction S'k-1
is orthogonal.
Hence Sk' is
an orthogonal set of nonzero vectors.
We have that span(Sk')
≤ span(Sk)
Sk' is
linearly independent by the theorem.
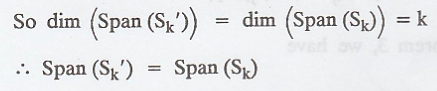
Note: The
construction of {v1, v2, ..., vn} by the use
of theorem is called the Gram-Schmidt process.
THEOREM 3.
Let V be a nonzero
finite-dimensional inner product space. Then V has an orthonormal basis β.
Furthermore, if β = {v1, v2, ..., vn} and x Є
V, then
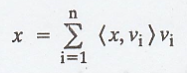
Proof:
Let β0
ordered basis for V.
Apply Theorem 2 to
obtain an orthogonal set β' of nonzero vectors with span(β') = span (β0)
= V.
By normalizing each
vector in β', we obtain an orthonormal set β that generates V.
By Corollary 2 to
Theorem 1, β is linearly independent; therefore β is an orthonormal basis for
V.
The remainder of the
theorem follows from Corollary 1 of Theorem 1.
Corollary:
Let
V be a finite-dimensional inner product space with an orthonormal basis β = {v1,
v2, ..., vn}.
Let T be a linear
operator on V, and let A = [T]β

Proof:
From Theorem 3, we have
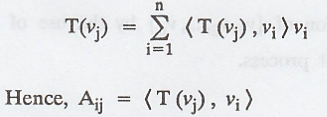
Definition :
Let β be an orthonormal
subset (possibly infinite) of a inner product space V, and let x Є V. We define
the Fourier coefficient of x relative to Є to be the scalars (x,y), where y Є
β.
Definition :
Let S be a nonempty
subset of an inner product space V.
We define ![]() (read "S perp") to be the set of all vectors in V that are orthogonal
to every vector in
(read "S perp") to be the set of all vectors in V that are orthogonal
to every vector in  for all y Є S}. The set
for all y Є S}. The set ![]() is called the
orthogonal complement of S.
is called the
orthogonal complement of S.
Note 1

Note 2

Note 3
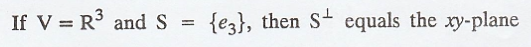
Theorem 4
Let W be a
finite-dimensional subspace of an inner product space V, and let y Є V. Then
there exist unique vectors u Є W and  such that y = u + z. Furthermore,
if {v1, v2, ..., vk} is an orthonormal basis
for W, then
such that y = u + z. Furthermore,
if {v1, v2, ..., vk} is an orthonormal basis
for W, then
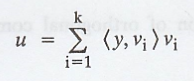
Proof
Let {v1, v2,
..., vk} be an orthonormal basis for W, let u be as defined in the preceding
equation, and let z = y-u.
Clearly u Є W and y = u
+ z.
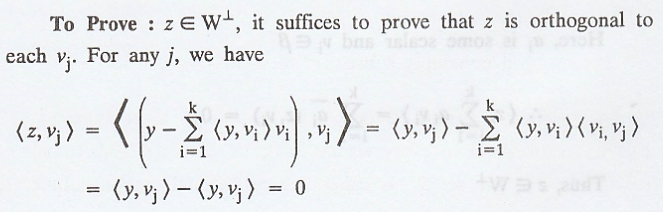

Theorem 5
Let β be a basis for
subspace W of an inner product space V, and let z Є V. Prove that  if
and only if <z,v> = 0 for every ν Є β.
if
and only if <z,v> = 0 for every ν Є β.
Proof :
Let β is a basis for a
subspace W of an inner product space V, and let z Є V.
To prove that  if and only if <z, v> = 0 for every v Є β
if and only if <z, v> = 0 for every v Є β
Necessary
condition :
Assume 
From the definition of
orthogonal complement, for every v Є β
Sufficient
condition :
Assume <z, v> = 0
for every v Є β
Since β is a basis for
a subspace W, every element in W can be written as,

Corollary
1.
Let W be a
finite-dimensional subspace of an inner product space V.
Prove that there exists
a projection T on W along ![]() that satisfies
that satisfies 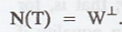 In addition, prove
that ||T(x)|| ≤ ||x|| for all x Є V.
In addition, prove
that ||T(x)|| ≤ ||x|| for all x Є V.
Proof :
Let W be a
finite-dimensional subspace of an inner product space V.


Let V be an inner
product space and suppose x and y are orthogonal vectors in V.

Corollary
2.
Let u unique is the
vector in W that is "closest" to y; that is, for any x Є W, ||y - x||
≥ ||y - u|| and this inequality is an equality if and only if x = u.
Proof :
As in Theorem 4, we
have that y = u + z, where  Let x Є W. Then u - x is orthogonal to z,
so, by corollary 1.
Let x Є W. Then u - x is orthogonal to z,
so, by corollary 1.
We have

Then the inequality
above becomes an equality, and therefore 
It follows that ||u -
x|| = 0, and hence x = u.
The proof of the
converse is obvious.
THEOREM 6.
Suppose that S = {v1,
v2, ..., vk} is an orthonormal set in an n-dimensional
inner product space V. Then
(a) S can be extended
to an orthonormal basis 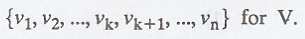
(b) If W = span(S),
then 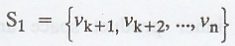 is an orthonormal basis for
is an orthonormal basis for ![]()
(c) If W is any
subspace of V, then dim(V) = dim(W) + dim(![]() ).
).
Proof :
(a) S can be extended
to an ordered basis

Now apply the
Gram-Schmidt process to S'.
The first k vectors
resulting from this process are the vectors in S and this new set spans V.
Normalizing the last n - k vectors of this set produces an orthonormal set that
spans V.
(b) Because S1
is a subset of a basis, it is linearly independent.
Since S1 is
clearly a subset of ![]() , we need only show that it spans
, we need only show that it spans ![]() .
.
Note that for any x Є
V, we have
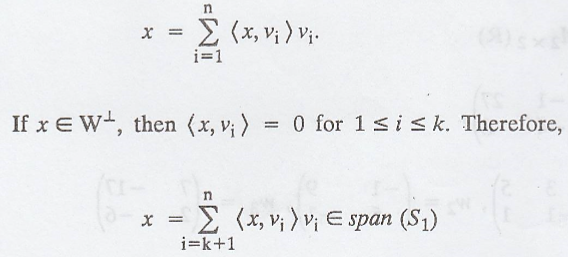
(c) Let W be a subspace
of V.
It is a
finite-dimensional inner product space because V is, and so it has an
orthonormal basis {v1, v2, ..., vk}. By (a)
and (b), we have

Random Process and Linear Algebra: Unit V: Linear Transformation and Inner Product Spaces,, : Tag: : - The Gram-Schmidt Orthogonalization Process and Orthogonal Complements
Related Topics
Related Subjects
Random Process and Linear Algebra
MA3355 - M3 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
