T linear, one-to-one, onto

(c) T linear, one-to-one, onto

Problem 1.

Suppose that T : R² → R² is linear, T(1, 0) = (1, 4) and T(1, 1) = (2, 5). What is T(2, 3)? Is T one-to-one?

Solution :

Given that T : R² → R² such that T(1, 0) = (1, 4),

T(1, 1) = (2, 5)

To find the value of T(2, 3) and check the transformation T is one-one or not.

Check that the set of domain vectors S = {(1, 0), (1, 1)} are linearly independent or not?

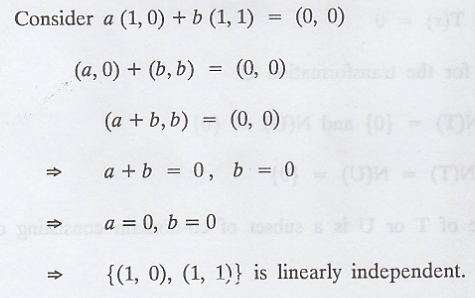
Therefore, the S = {(1, 0), (1, 1)} is linearly independent .......(1)

Further, the dimension of R² is 2 which is equals to the number of vectors in S.

So, S spans R² ........(2)

From (1) and (2) confirms that S is the basis to R².

So, every vector in the domain R² can be written as a linear combination of vectors in S.

Let (a, b) be any vector in R³

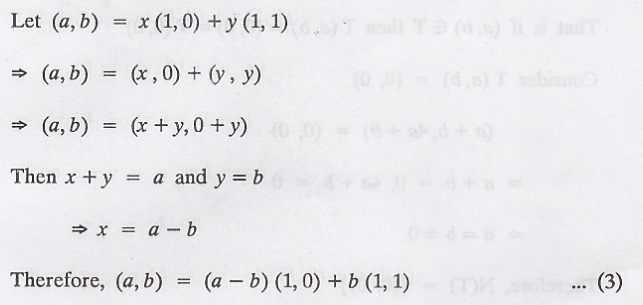
Given that T is a linear transformation.

Apply linear transformation on (3), then

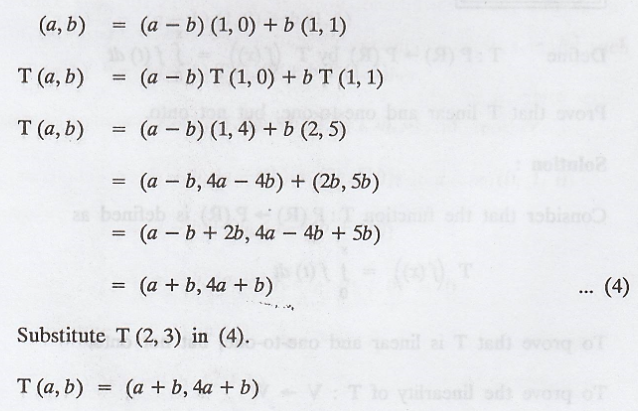
Check the transformation T is one-one or not.

A linear transformation T is one-one if and only if N(T) = {(0, 0)}

Hence, the transformation T is one-one.

Problem 2.

Prove that T linear and one-to-one; but not onto.

Solution :

Consider that the function T : P(R) → P(R) is defined as

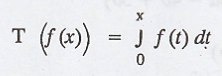
To prove that T is linear and one-to-one, but not onto.

To prove the linearlity of T: V → W

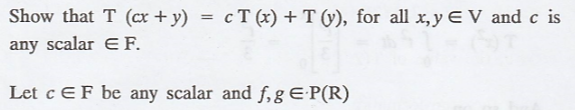
Now,

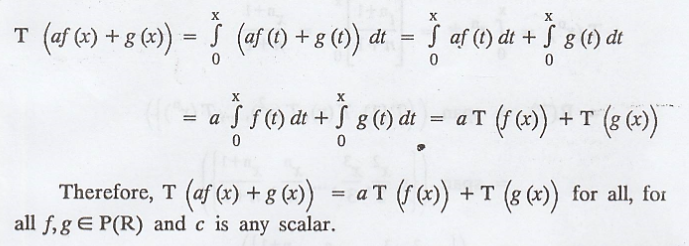
Hence, T is a linear transformation.

Now prove that T is one-to-one.

The linear transformation T is one-to-one if and only if N(T) = {0}

To find the basis for the range of T.

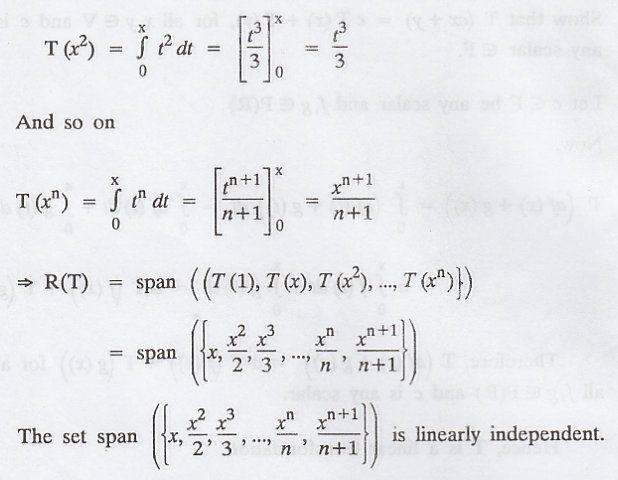
Thus, the dimension of the range of T, i.e., rank (T) = n + 1.

The dimension theorem states that if V and W are the vector spaces and if T: V → W is linear.

Let V is the finite-dimensional then,

N(T) + R(T) = dim (V).

Since dim(P (R)) = n + 1 and rank(T) = n + 1

So by the Dimension theorem.

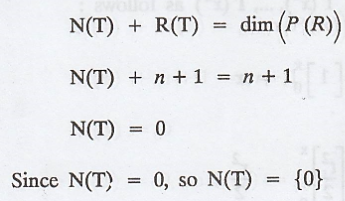
Since N(T) = {0}, so T is one-to-one.

The basis for P(R) (domain) is span ((1, x, x², ..., xⁿ) and the basis for the codomain P(R) is span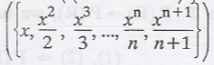 

Therefore, T is not onto, because no integral is equal to 1.

Problem 3.

Let T : P(R) → P(R) be defined by T(f(x)) = f '(x). Recall that T is linear. Prove that T is onto, but not one-to-one.

Solution :

Let T : P(R) → P(R) be defined by T(f(x)) = f'(x)

To prove that T is onto, but not one-to-one.

Note g(x) = 3 and h (x) = 4 both belongs to P(R) and g(x) ≠ h(x).

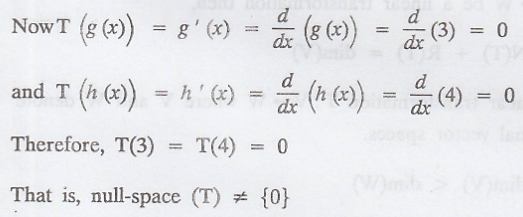
Hence, T is not one-to-one.

To prove that T is onto.

For any element g(x) in P(R), we can find f(x) = ∫ g(x) dx in P(R) which satisfies that

T(f(x)) = f'(x) = g(x)

Therefore, g(x) is in Range (T)

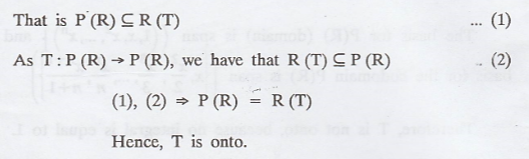
Problem 4

Let V and W be finite-dimensional vector spaces and T : V → W be linear.

Prove that if dim(V) < dim(W), then T cannot be onto.

Solution :

We know that,

Dimension theorem: Let V be a finite dimensional vector space and let T: V → W be a linear transformation then,

N(T) + R(T) = dim(V)

Let the linear transformation T: V → W where V and W denote finite dimensional vector spaces.

Let dim(V) < dim(W)

To prove : T is not onto

Suppose that T is onto. Then,

R(T) = dim(W) ..........(1)

Also, by dimension theorem,

R(T) + N(T) = dim(V)

Since dimension is a non-negative number

→ N(T) = {0}

→ R(T) = dim(V)

Equivalently,

dim(T) = dim(V) .......(2)

From (1) and (2) → dim(V) = dim(W)

But, this is contradiction to the hypothesis; dim(V) < dim(W)

Hence, T is not onto.

Problem 5.

Prove that if dim(V) > dim(W), then T cannot be one-to-one.

Solution :

Let dim(V) > dim(W)

To prove : T is not one-to-one.

Suppose T is one-one.

N(T) = 0

Also since V finite dimensional so T is onto also.

Now, by dimension theorem,

R(T) + N(T) = dim(V)

═> R(T) = dim(V)

Also, T is one-to-one.

═> R(T) = dim(W)

Consequently,

dim(V) = dim(W)

Which contradicts to the fact that dim(V) > dim(W)

Hence, T is not one-to-one.