T is unique

(f) T is unique

Theroem :

Let V and W be vector spaces over F, and suppose that {v₁, v₂, …, v_n} is a basis for V. For w₁, w₂, …., w_n in W, there exists exactly one linear transformation T : V →  W such that T(v_i) = w_i for I = 1, 2, …, n

Proof :

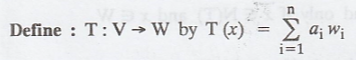
(a) T is linear: Suppose that u, v Є V and d Є F.

Then we may write

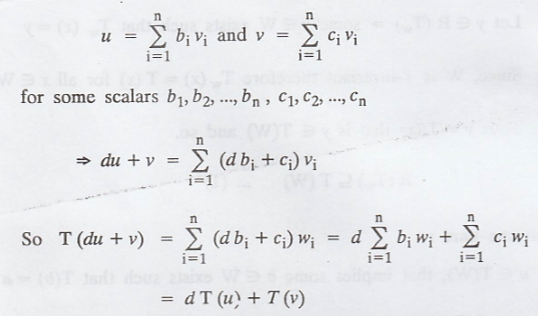
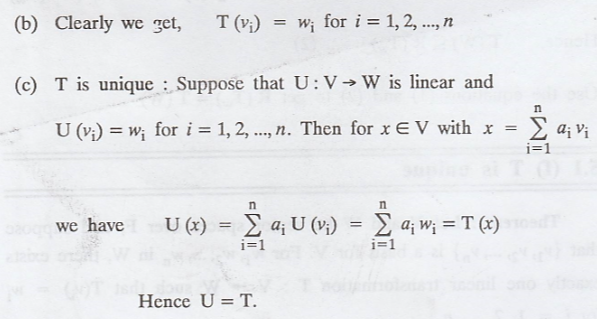
Note: Let V and W be vector spaces, and suppose that V has a finite basis {v₁, v₂, ... , v_n}. If U, T: V → W are linear and U(v_i) = T(v_i) for i 1, 2,...n, then U = T.

Problem 1.

Let V and W be vector spaces over a common field, and let β be a basis for V. Then for any function f : β → W there exists exactly one linear transformation T : V → W such that T(x) = f(x) for all x Є β.

Solution :

Let the linear transformation, T: V → W and f : β → W

Take the linear combination,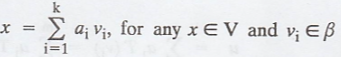 

by Definition of Linear transformation

So, that 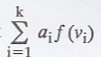 is a fixed vector in V.

Hence, the linear transformation is unique.

(g) Direct sum, quotient space

Problem 1.

Let V be a finite-dimensional vector space and T : V → V be linear.

Suppose that V = R(T) + N(T) prove that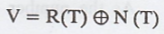 

Solution :

Let V be a finite dimensional vector space and T: V → V be linear.

Let V = N(T) + R(T)

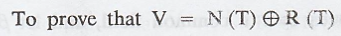
Let the dimension of V be n.

Let v = {v₁, v₂, ..., v_n} is a basis for N(T).

By extending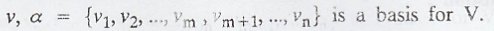 

For any vector u in R(T).

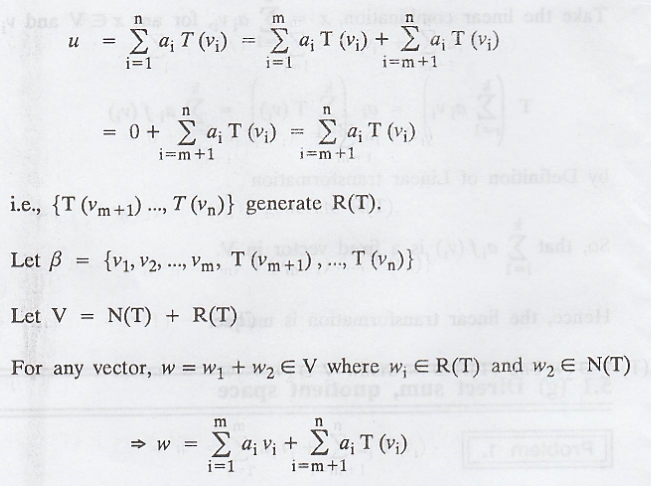
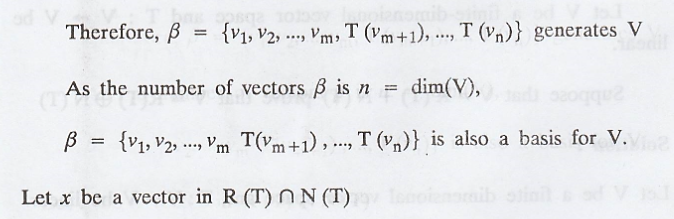
Problem 2

Let V be a finite-dimensional vector space and T : V →  V be linear.

Suppose that R(T) ∩ N(T) = {0}. Prove that V = R(T) eeee N(T)

Solution :

Suppose that R(T) ∩ N(T) = {0}. Then dim (R(T) ∩ N(T)) = 0

We know that,

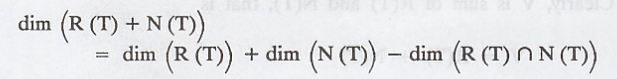
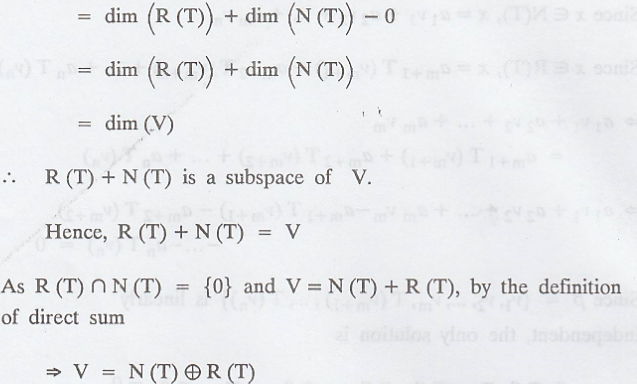
Problem 3

Let V be a finite dimensional vector space and T : V → V be linear prove that V = R(T) + N(T), but V is not a direct sum of these two spaces.

Solution :

Let the finite dimensional vector space V.

Problem 4.

Let V be a finite-dimensional vector space and T : V → V be linear.

Find a linear operator T₁ on V such that R(T₁) ∩ N(T₁) = {0} but V is not a direct sum of R(T₁) and N(T₁). Conclude that V being finite-dimensional is also

Solution :

Let the function, T₁ : V → V, such that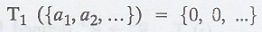 

Suppose R(T₁) = 

EXERCISE 5.1

1. Label the following statements as true or false. In each part, V and W are finite-dimensional vector spaces (over F), and T is a function from V to W.

(i) If T is linear, then T preserves sums and scalar products.

(ii) If T is linear, then T (0_V) = 0_W

(iii) If T(x + y) = T(x) + T(y), then T is linear.

(iv) If T is linear, then T carries linearly independent subsets of V onto linearly independent subsets of W.

(v) T is one-to-one if and only if the only vector x such that T(x) = 0 is x = 0

State why T is not linear.

3. Let V and W be vector spaces. Then the dimension of L(V, W) is dim V x dim W.

4. Which of the following functions are linear transformations ?

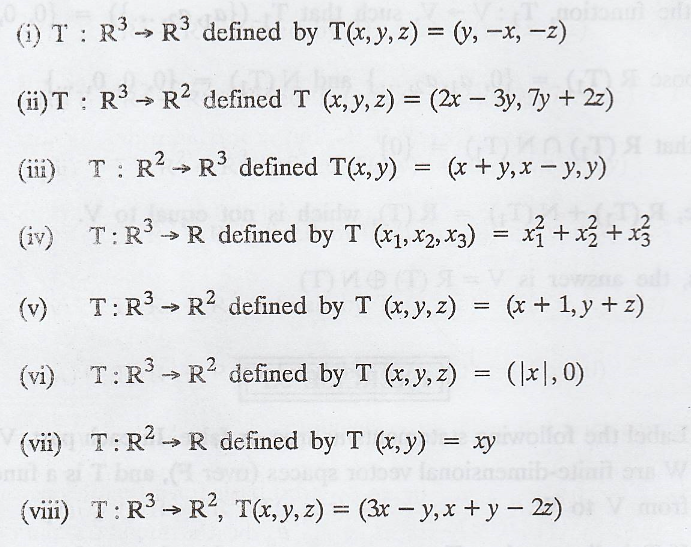
5. Show that the transformation T : R² → R³ defined by T(x, y) = (x, x-y, x+y) is a linear transformation and is one-to-one but not onto.

6. Show that the transformation T : R³ → R² defined by T(x₁, x₂, x₃) = (x₁,x₂) is a linear transformation and is onto but not one to one.