Random Process and Linear Algebra: Unit V: Linear Transformation and Inner Product Spaces,,
T is Linear
Problems of Linear
Details about T is linear and its problems
(a) T is linear

Problem 1

Solution :
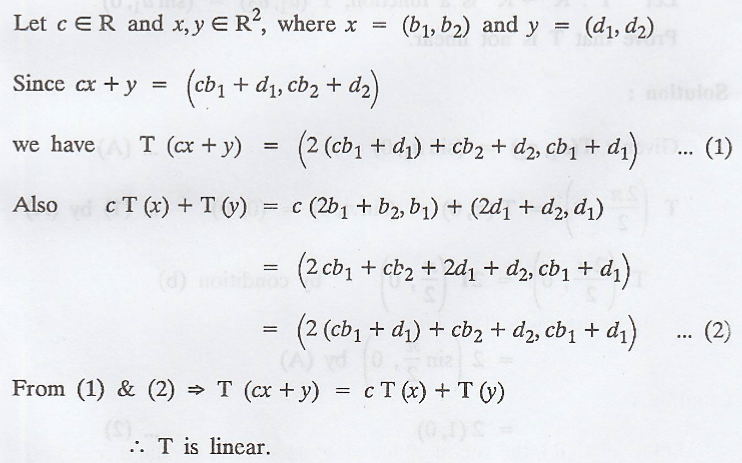
Problem 2
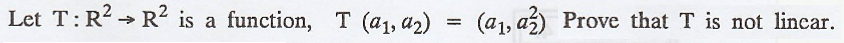
Solution :
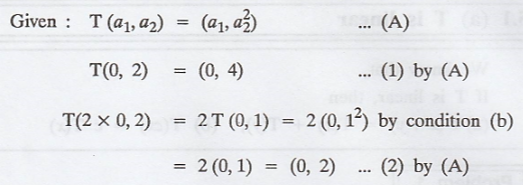
Here, (1) ≠ (2) => Condition (b) is not
satisfied.
So, T is not linear.
Problem 3.
Let  Prove that T is not linear.
Prove that T is not linear.
Solution :
Here, (1) ≠ (2) => Condition (b) is not satisfied.
So, T is not linear.
Problem 4.
Let  Show that T is not linear.
Show that T is not linear.
Solution :

Here, (1) ≠ (2) => Condition (b) is not
satisfied.
So, T is not linear.
Problem 5.
Prove that there exists a linear transformation T : R2
→ R3 such that T(1, 1) = (1, 0, 2) and T(2, 3) = (1, -1, 4). What is
T(8, 11)?
Solution :
Given: The transformation T : R2 → R3
is defined by,
T(1, 1) = (1, 0, 2) and T(2, 3) = (1, -1, 4)
To prove that the transformation T is linear, and
then find the value of T(8, 11).
First, prove that if the set S = {(1, 1), (2, 3)} is
linearly independent.

Whenever a(1, 1) + b(2, 3) = (0, 0), the result
would be a = 0, b = 0
=> S = {(1, 1), (2, 3)} is linearly independent.
Furthermore, the dimension of R2 = 2 =
number of vectors in S.
=> S spans R2.
Therefore, S is the basis for R2.
So, every vector in the domain R2 can be
written as a linear combination of these vectors.
Therefore, it proves that the transformation T is
linear.
Let (a, b) be any vector in R2. Then,
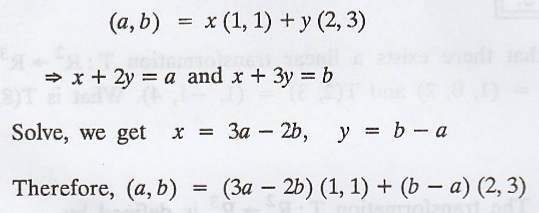
Take T on both sides, we get
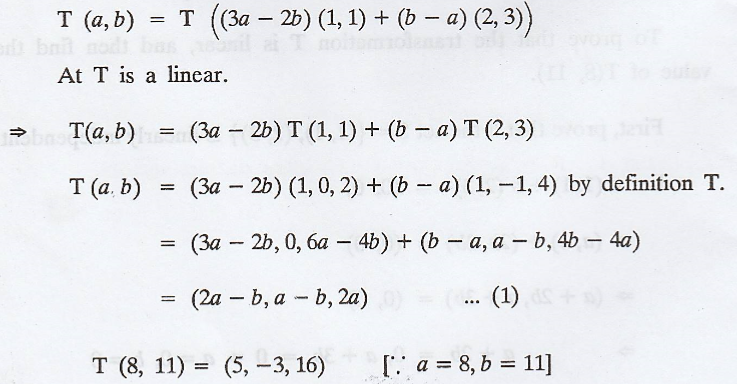
Problem 6.
Is there a linear transformation T : R3 →
R2 such that T(1, 0, 3) = (1, 1) and T(-2, 0, -6) = (2, 1)?
Solution :
We know that,
If T is linear, then
(a) T(x + y) = T(x) + T(y)
(b) T(cx) = c T(x)
Given:
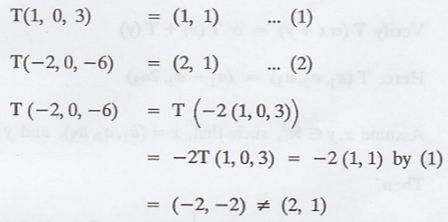
So, T is not linear.
Problem 7.
Prove that there is an additive function
i.e., T(x,y) = T(x) + T(y). T : R → R that is not
linear.
Solution :
Let T : R → R, Suppose x, y Є R are distinct
vectors.
Define by T(v) = f(v) for all v Є V. So that, T is
an additive.
Prove that T is not linear.
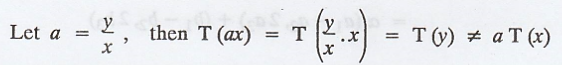
Hence, T is not linear.
Problem 8.
Let 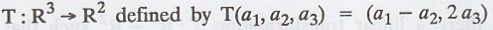
Prove that T is linear.
Solution :

Verify T(ax+y) = a T(x) + T(y)

Then
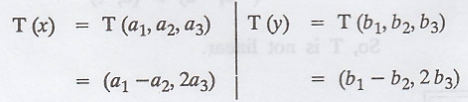
And
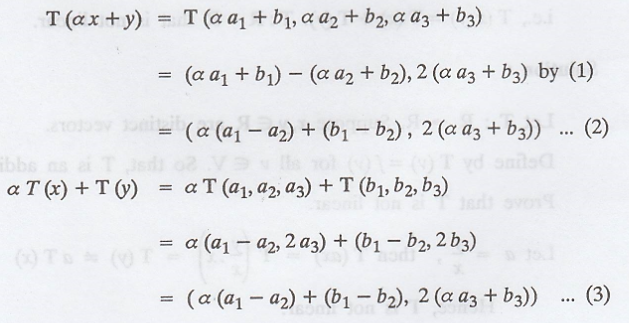
From (2) & (3) we get
T(ax + y) = a T(x) + T(y) To
Hence, the transformation T: R3 → R2;
defined by  is linear.
is linear.
Problem 9.
Let T: R2 → R3 defined by 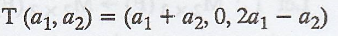 Prove that T is linear.
Prove that T is linear.
Solution :
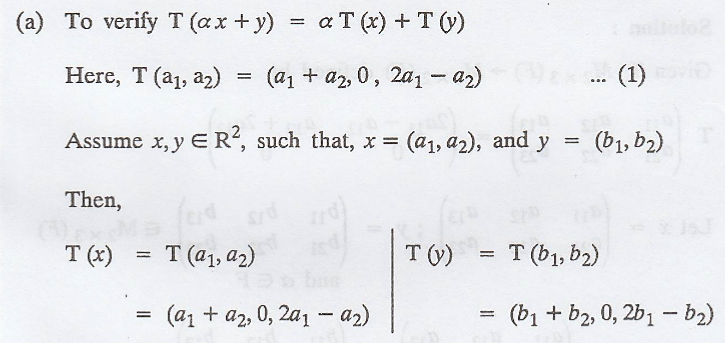


Problem 10
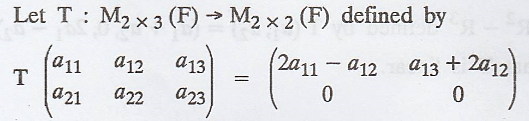
Prove that T is linear
Solution :


Also
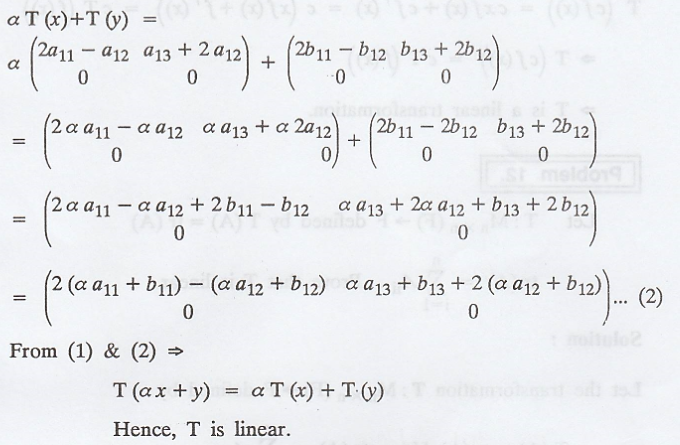
Problem 11
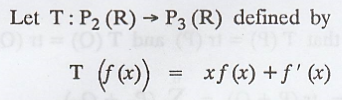
Prove that T is linear
Solution :
Given that 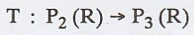 defined by
defined by 
To prove T is linear, we consider
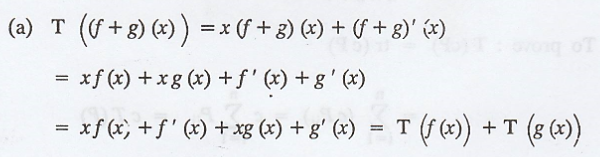
First part of the definition is satisfied.
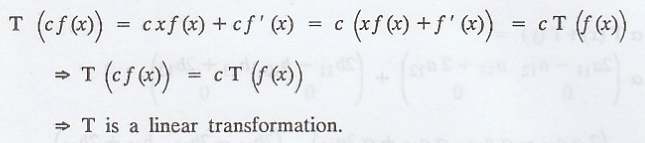
Problem 12.

Solution :
Let the transformation T : Mn x n(F) → F
defined by

To prove that T(A) = tr(A) is linear transformation.
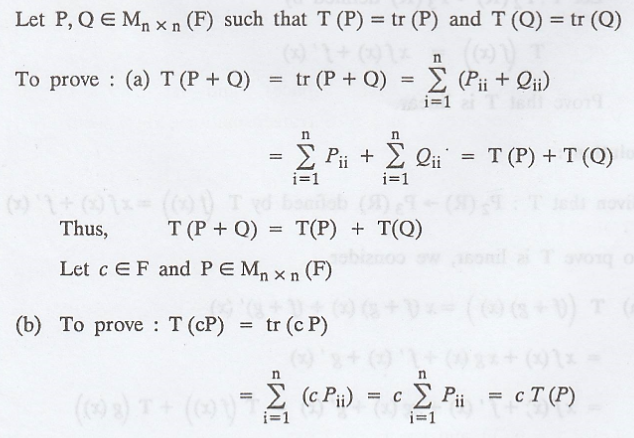
Thus, T(c P) = c T(P)
=> T(A) = tr(A) satisfies the properties that
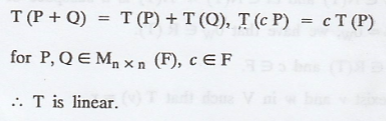
Random Process and Linear Algebra: Unit V: Linear Transformation and Inner Product Spaces,, : Tag: : Problems of Linear - T is Linear
Related Topics
Related Subjects
Random Process and Linear Algebra
MA3355 - M3 - 3rd Semester - ECE Dept - 2021 Regulation | 3rd Semester ECE Dept 2021 Regulation
