Strictly Stationary Processes

STRICTLY STATIONARY PROCESSES

(a) Stationary process (or) Strictly stationary process (or) Strict sense stationary process [SSS processes] [A.U. N/D. 2004, M/J 2014]

"If a random process is stationary to all order then the random process is said to be strict sense stationary process."

Note: 1. In general we consider upto second order density function or second order characteristics to verify whether a process to be stationary or not in the respective order.

2. If a random process fails to be atleast first order stationary then the random process is not a stationary process.

(b) Jointly stationary in the strict sense.

Two real-valued random processes {X(t)} and {Y(t)} are said to be jointly stationary in the strict sense, if the joint distribution of X(t) and Y(t) of all order are invariant under translation of time.

(c) First order stationary process

A random process is called stationary to order one, if its first-order density function does not change with a shift in time origin.

In otherwords,

f_x(x₁:t₁)= f_x(x₁:t₁ + ∆) must be true for any t₁ and any real number ∆ then X (t) is to be a first order stationary process.

Theorem 1: A first order stationary random process has a constant mean. (OR) The first order stationary random process X(t) has independent of t.

Let X (t) be a first order stationary random process

=> f(x, t + ε) = f(x, t) ............(1) where t, ε are arbitrary.

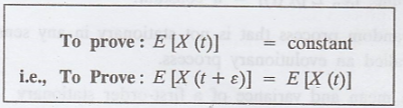
Proof :

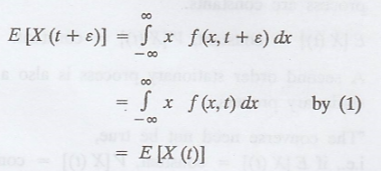
Hence, E [X (t)] = constant.

Theorem 2: A first order stationary random process has a constant variance.

Let X (t) be a first order stationary random process.

→ f(x, t + ε) = f(x, t) ............(1) where t, ε are arbitrary.

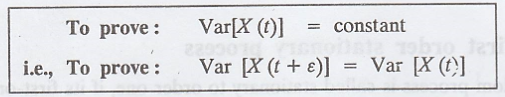
Proof :

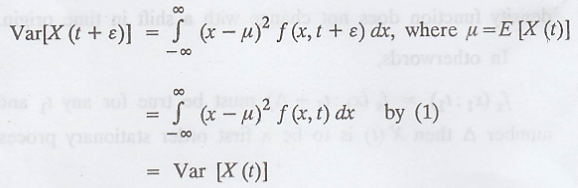
Hence, Var [X (t)] = constant.

STATIONARY PROCESS

Formula: E[X(t)] = Constant and V[X(t)] = Constant

Note 1 : First-order densities of a SSS process are independent of time. i.e., E [X (t)] = a constant.

Note 2 : A random process that is not stationary in any sense is called an evolutionary process.

Note 3 : The mean and variance of a first-order stationary process are constants.

E [X (t)] = constant, V[X (t)] = constant.

Note 4 : A second order stationary process is also a first order stationary process.

"The converse need not be true, i.e., if E [X (t)] = constant, V[X (t)] = constant, then X (t) need not be a SSS process."

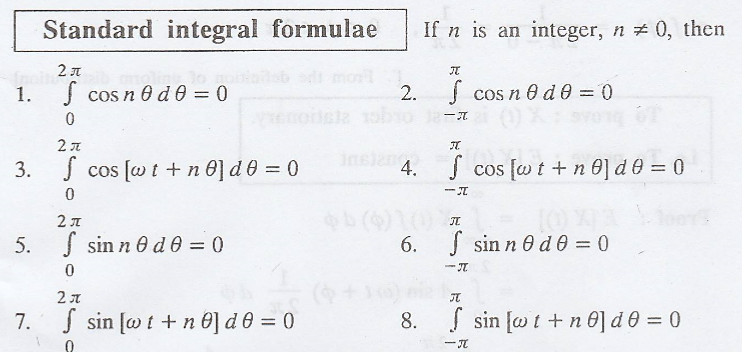
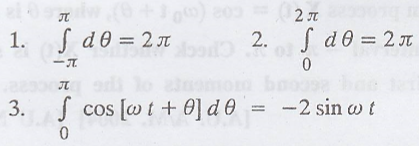
I. Example for First Order Stationary Process

Example 3.2.1

Show that the random process X (t) = A sin (ωt + φ) where A and ω are constants, φ is a random variable uniformly distributed in (0, 2π) is first order stationary.

Solution:

Given: X (t) = A sin (ωt + φ)

where 'φ' is uniformly distributed in (0, 2π)

Proof :

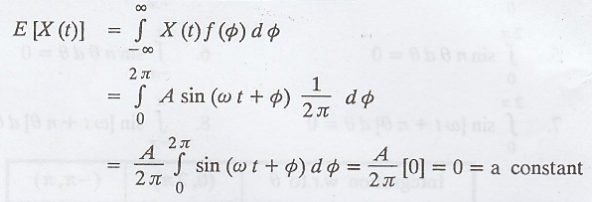
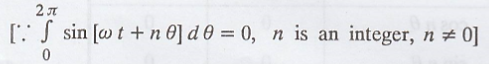
Hence, X (t) is a first order stationary process.

II. Example for SSS Process

Example 3.2.2

Consider the random process X(t) = cos (ω₀t + θ), where θ is uniformly distributed in the interval -л to л. Check whether X(t) is stationary or not? Find the first and second moments of the process. [A.U. A/M. 2004] [A.U N/D 2010]

Solution:

Given: X (t) = cos (ω₀t + θ), where 'θ' is uniformly distributed in (−л, л)

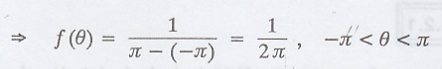
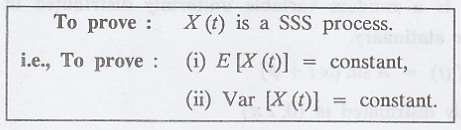
Proof:

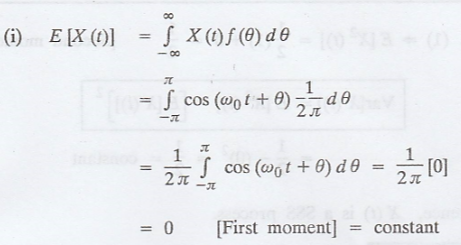
(ii)

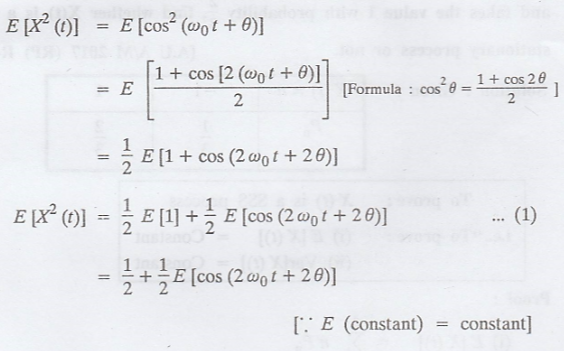
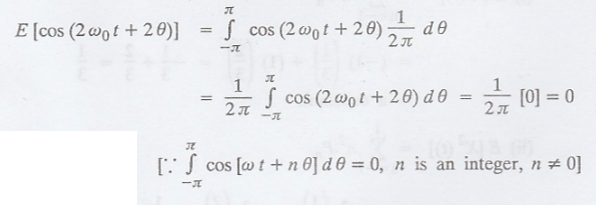
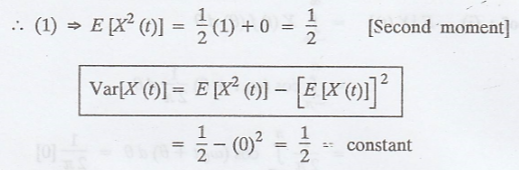
Hence, X (t) is a SSS process.

Example 3.2.3

If the random process X(t) takes the value -1 with probability 1/3 and takes the value 1 with probability 2/3, find whether X(t) is a stationary process or not. [A.U A/M 2017 (RP) R-13]

Solution:

Given:

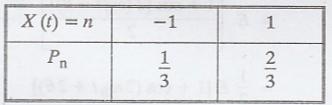
Proof :

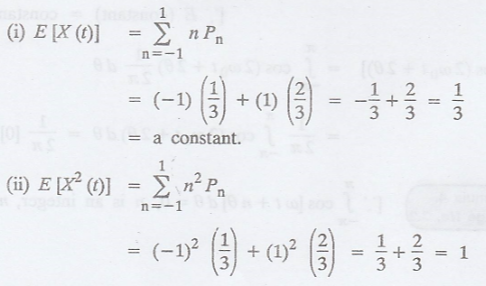
Example 3.2.4

Show that, if the process X(t) = a cos ωt + b sin ωt is SSS, where 'a' and 'b' are independent random variables, then they are normal.

Solution:

Given: X(t) = a cos ωt + b sin ωt

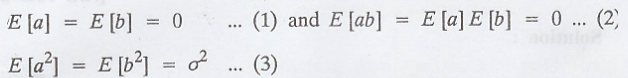
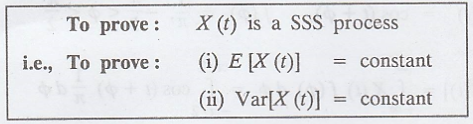
Proof

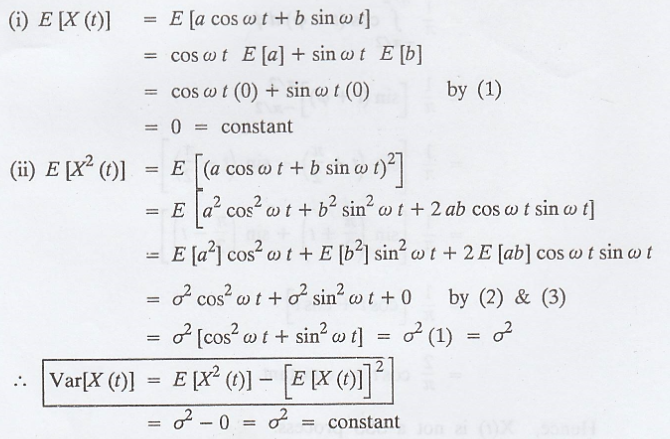
Hence, X(t) is a SSS process.

III. Example for not SSS process

Example 3.2.5

Consider the random process X (t) = cos (t + φ), where is a φ random variable with density function f(φ) = 1/π, -π/2 < φ < π/2, check whether the process is stationary or not. [A.U. May 2000] [A.U CBT M/J 2010, A.U Tvli. A/M 2009] [A.U N/D 2010]

Solution :

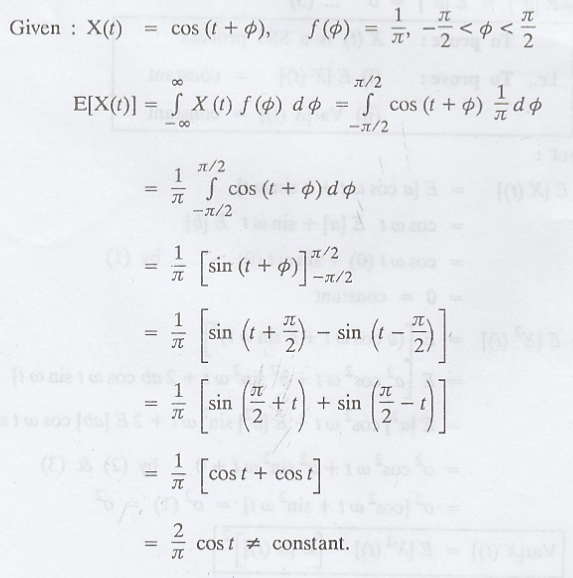
Hence, X(t) is not a SSS process.

Example 3.2.6

The process {X(t)} whose probability distribution under certain conditions is given by, 

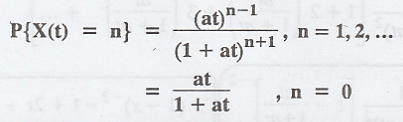 Show that it is "not stationary" (or evolutionary). 

[A.U. M/J 2006] [A.U. N/D 2007] [A.U. A/M 2008] [A.U Tvli M/J 2010, Trichy A/M 2010, N/D 2010, N/D 2011] [A.U M/J 2012, N/D 2012, N/D 2013, M/J 2014, N/D 2014] [A.U N/D 2015 R-13] [A.U N/D 2016 R-13 RP] [A.U A/M 2017 R-08] [A.U N/D 2017 R-13]

Solution:

The probability distribution of X(t) is

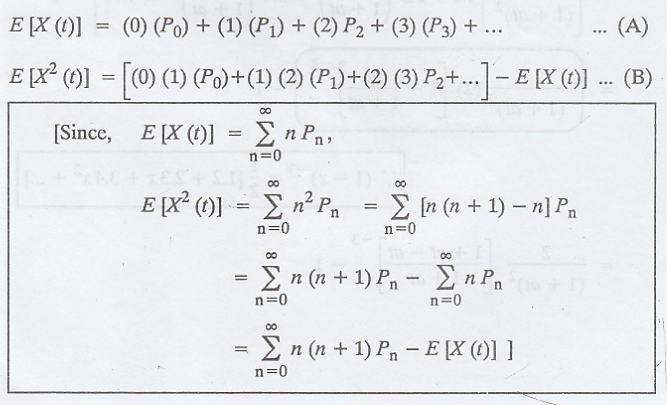
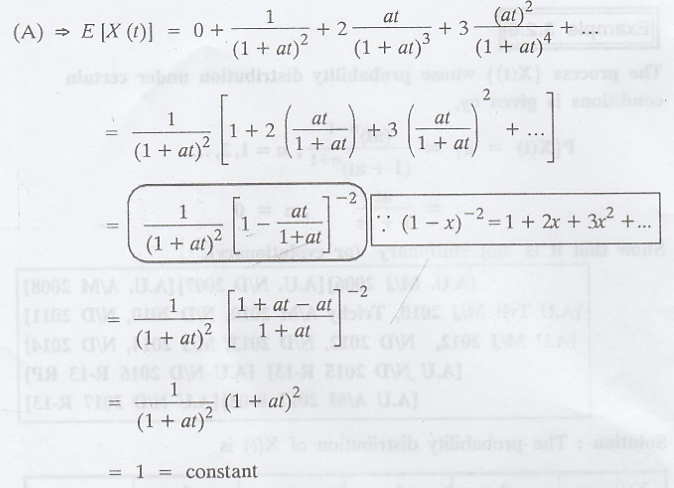
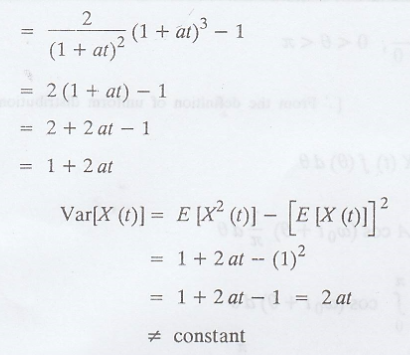
Here, E [X (t)] = constant but Var [X (t)] ≠ constant.

.'. The given process is not a stationary process.

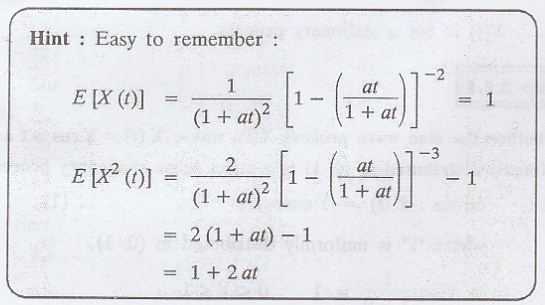
Example 3.2.7

Show that the random process X(t) = A cos (ω_ot +  θ) is not stationary, if A and ω_o are constants and θ is uniformly distributed random variable in (0,л) [AU Dec. 2005, April 2007]

Solution :

Given: X (t) = A cos (ω_ot + θ),

where 'θ' is uniformly distributed in (0, л).

Example 3.2.8

Verify whether the sine wave process X(t), where X(t) = Y cos ωt and Y is uniformly distributed in (0, 1) is a strict sense stationary process.

Solution :

Given: X(t) = Y cos ωt, ..............(1)

where 'Y' is uniformly distributed in (0, 1).

Example 3.2.9

A random process has sample functions of the form X(t) = A cos(ωt + θ) in which A and ω are constants and θ is a random variable. Prove this process is not stationary, if it is uniformly distributed over a range of 2л.

Solution:

It is given that the random variable is not uniform distributed.

Let the distribution be ƒ(θ), it is not a constant.

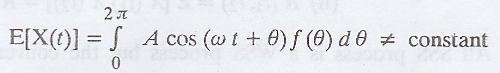
This involves a time component and is not constant which indicates that the process is not a stationary process.

EXERCISE 3.2

1. Define a strict-sense stationary process and give an example.

2. Define a k^th order stationary process. When will it become a SSS process ?

3. What is the first order stationary process?

4. Show that the random process X(t) = 100 sin (ω t + θ) is first order stationary, if it is assumed that ω is constant and θ is uniformly distributed in (0, 2 л).

5. Consider the random process X (t) = A cos (ωt + φ), where ω is a random variable with density functions f(w) and φ a random variable uniform in the interval (-л, л) and independent of ω, prove that X (t) is a first order stationary with zero means.

6. Consider the process X(t) = 10 sin (200t + φ), where φ is uniformly distributed in the interval (-л, л). Check whether the process is stationary or not.

7. Give an example of stationary random process and justify your claim. [A.U N/D 2005]